Как называется случайное событие, вероятность которого равна нулю
 Скачать 62 Kb. Скачать 62 Kb.
|
|
Укажите формулу классического определения вероятности случайного события А (n-общее число исходов, m-число благоприятных исходов для события А). 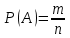 Как называется случайное событие, вероятность которого равна нулю? невозможным Как называется случайное событие, вероятность которого равна единице? Достоверным События называют совместными, если: наступление одного из событий в одном опыте не исключает появление другого События называют единственно возможными: если в условиях данного опыта произойдут только эти события и никакие другие Статистическая вероятность события численно равна (n-общее число исходов, m-число исходов для события А): 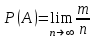 Суммой двух событий A и B является событие C, которое заключается: в появлении либо события А, либо события В Произведением двух событий A и B является событие С, которое заключается: в одновременном появлении событий А и В Вероятность суммы двух совместимых событий равна: P (A или B) = P(A)+ P(B)- P(A и B) Вероятность суммы двух несовместимых событий равна: P (A или B) = P(A)+P(B) Вероятность произведения двух независимых событий равна: P(AиB) = P(A)*P(B) Вероятность произведения двух зависимых событий равна: P(AиB) = P(A)*P(B/A) Случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями, называют Дискретной Случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка, называют Непрерывной Дисперсия характеризует: степень рассеяния случайной величины относительно её математического ожидания Дисперсия дискретной случайной величины рассчитывается по формуле: 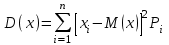 Дисперсия непрерывной случайной величины рассчитывается по формуле: 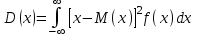 Дискретная случайная величина не подчиняется: нормальному распределению Математическим ожиданием случайной величины называется: сумма произведений всех возможных значений случайной величины на соответствующие им вероятности Математическое ожидание дискретной случайной величины рассчитывается по формуле: 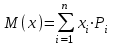 Математическое ожидание непрерывной случайной величины рассчитывается по формуле: 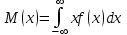 Среднее квадратичное отклонение дискретной случайной величины рассчитывается по формуле: 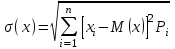 Среднее квадратичное отклонение непрерывной случайной величины рассчитывается по формуле: 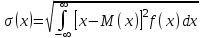 Установите правильную последовательность следующих этапов статистической работы:1.обработка данных 2.сбор данных 3.выводы, прогнозы. 213 Коэффициент Стьюдента находят из таблицы по значениям: доверительной вероятности и объёма выборки Зависимость называется функциональной, если: одному значению одной переменной величины соответствует одно значение другой Если одному значению одной переменной соответствует множество значений другой, то такая зависимость называется: статистической Метод регрессии позволяет установить: количественное изменение среднего значения одной величины по мере изменения другой Линейный коэффициент корреляции определяется по формуле: 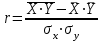 По формуле 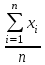 находят: находят: среднее значение выборки По формуле 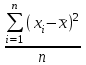 находят: находят:дисперсию выборки Статистическая совокупность, которая включает в себя все изучаемые объекты, называется: генеральной совокупностью Статистическая совокупность, которая включает в себя не все изучаемые объекты, а лишь их часть, называется: Выборкой Интервал возможных значений искомого параметра, в котором могут находиться с некоторой вероятностью его значения, называется: доверительным интервалом Коэффициент линейной корреляции может принимать значения: от 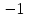 до +1 до +1Коэффициент, характеризующий силу статистической линейной связи между случайными величинами, называется: коэффициентом регрессии Что понимается под случайным событием? событие, которое в результате опыта может произойти или не произойти Что такое вероятность случайного события? это численная мера степени объективной возможности этого события Какие значения может принимать вероятность случайного события? от 0 до 1 События называются несовместными, если: никакие два из них не могут появиться вместе События называют равновозможными, если: вероятности этих событий одинаковы События называются противоположными, если: одно событие заключается в непоявлении другого события События называются независимыми, если: появление одного из них не меняет вероятности появления другого Вероятность события А, вычисленная при условии, что событие В произошло, называется: условной вероятностью события А В каком из представленных случаев перечисленные события не образуют полную группу событий? оценка за ответ на экзамене: А – три; В – два К экзамену студент выучил 20 билетов из 30. Найти вероятность, что ему достанется невыученный билет: 1/3 Вероятность поступления хотя бы одного вызова врача в течение часа равна 0,85. Найти вероятность того, что в течение часа не последует ни одного вызова: 0,15 Найти вероятность того, что в семье с тремя детьми все трое сыновья (считать, что вероятность рождения мальчика равна 0,515): 0,136 Медсестра обслуживает три палаты. Если поступает вызов, то вероятность того, что он будет из первой палаты – 0,2; из второй – 0,4. Какова вероятность того, что вызов будет из третьей палаты? 0,4 Случайная величина – это: величина, которая в результате опыта может принять то или иное значение, заранее неизвестно какое именно Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется: законом распределения случайной величины Таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности, называется: рядом распределения случайной величины Функция вида F(х) = P (X<x), где Х – случайная величина, называется: дисперсией случайной величины Функция распределения вероятности случайной величины может принимать значения, лежащие в интервале: от 0 до 1 Функция вида 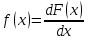 , где x – случайная величина, а F(x)- функция распределения вероятности называется: , где x – случайная величина, а F(x)- функция распределения вероятности называется: плотностью распределения вероятности случайной величины Плотность распределения вероятности случайной величины может принимать значения, лежащие в интервале: от 0 до + 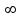 Число, к которому стремится среднее значение случайной величины при бесконечном числе наблюдений, называется: математическим ожиданием случайной величины Степень разброса случайной величины относительно ее математического ожидания характеризуется: дисперсией случайной величины Наиболее вероятное значение случайной величины называется: модой случайной величины К случайной величине Х прибавили постоянную величину A. Как от этого изменится ее математическое ожидание? увеличится на A К случайной величине Х прибавили постоянную величину A. Как от этого изменится ее дисперсия? не изменится Повторяющиеся значения выборки, расположенные в порядке возрастания, называются: вариационным рядом Значения, с помощью которых из данных выборки приблизительно определяют числовые характеристики генеральной совокупности, называются: оценками Отклонение результатов измерения от истинного значения измеряемой величины называется: погрешностью измерения Уравнение линейной регрессии это: 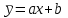 Сумма вероятностей противоположных событий равна: 1 Вероятность какого события не может быть равна 0,3? Достоверного Из 800 больных, поступивших в хирургическое отделение за месяц, 300 имели травмы. Какова относительная частота поступления больных с этим видом заболевания (ответ числом)? 0,375 Случайная величина задана законом распределения:
Чему равно математическое ожидание этой величины? 1,2 Какая из перечисленных величин являются дискретной? частота пульса Чему равно среднее квадратическое отклонение случайной величины, если ее дисперсия равна 0,25? (ответ дать числом) 0,5 Чему равна вероятность выпадения числа 3 при одном бросании игральной кости? 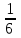 Чему равна вероятность выпадения суммы очков равной 3 при одном бросании двух игральных костей? 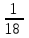 Если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине практически не превосходит: 3 Если у случайной величины, распределенной по нормальному закону, математическое ожидание увеличилось на две единицы, то как изменится положение графика функции распределения плотности вероятности? сместится вправо по оси Х на две единицы При каком значении случайной величины Х, функция Гаусса - f(x) всегда принимает максимальное значение? Х= математическому ожиданию Площадь фигуры, ограниченная графиком функции Гаусса и осью ОХ равна (ответ дать числом) 1 Сумма этих двух событий – достоверное событие, произведение этих двух событий - невозможное событие. Эти два события являются: Противоположными Выборка правильно отражает пропорции генеральной совокупности. Это означает, что она Репрезентативна Что понимается в статистике под термином «вариация показателя»? изменение величины показателя Термин регрессия в статистике понимают как: а) функцию связи, зависимости; б) направление развития явления вспять; в) функцию анализа случайных событий во времени; г) уравнение линии связи а, г Назовите основные виды ошибок регистрации: а) случайные; б) систематические; в) ошибки репрезентативности; г) расчетные а, б, в, Выборочная совокупность отличается от генеральной: разным объемом единиц непосредственного наблюдения Дисперсия постоянной величины равна (ответ дать числом) 0 Интеграл от плотности распределения вероятности f(x) непрерывной случайной величины 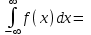 1 Математическое ожидание постоянной величины равно самой величине Если математическое ожидание оценки равно значению оцениваемого параметра, то такая оценка является Несмещенной Условная вероятность P(A/B) это: вероятность события А, вычисленная в предположении, что событие В уже произошло Уравнение регрессии имеет вид – Y=5,1-1,7*х. Оно показывает, что при увеличении Х на 1 единицу своего измерения Y в среднем: уменьшится на 1,7 единиц своего измерения Вероятности того, что студент сдаст каждые из 3-х экзаменов сессии на отлично равны соответственно 0,4; 0,5; 0,2. Получения отличных оценок на этих экзаменах - события независимые. Вероятность того, что студент сдаст на отлично все 3 экзамена, равна (ответ числом) 0,04 Медсестра обслуживает две палаты. Вероятность поступления вызова из первой палаты – 0,2; из второй – 0,1. Обращение пациентов события независимые. Вероятность того, что за вызов поступит хотя бы из одной палаты равна 0,28 Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна (ответ дать числом) 0 Вероятность попадания случайной величины X, заданной функцией распределения вероятности F(x) в полуинтервал [a;b), вычисляется по формуле: P(aX Вероятность попадания случайной величины X, заданной функцией плотности распределения f(x) в интервал (a; b), вычисляется по формуле:  |
