Как НОД и НОК помогают решать разнообразные интересные задачи. Как НОК и НОД чисел помогает решать разнообразные интересные зад. Как нок и нод чисел помогает решать интересные и разнообразные задачи
 Скачать 173 Kb. Скачать 173 Kb.
|
|
0 НОД(30n+2; 12n+1)=НОД(1 ;6n)= 1 Т.е. дробь несократима. ч.т.д Задачи на нахождение НОД №1 Найдите НОД(2100-1;2120-1) Решение: 2120-1=2120220-220+220-1=220(2100-1)+(220-1). Обозначим п=2100-1 Имеем НОД(п;220п+220-1)=НОД(п;220-1). В этом случае найдем п 2100-1=(220)5-15=(220-1)(...)т.е. НОД(2100-1;2120-1)=220-1 Ответ:d=220-1 №2 Найти НОД(11..11;11...1)(100 и 60 единиц) 1 способ. Решение. Соответственно на эти числа может делиться а=11 ...1( п - единиц) И с помощью чисел 100 и 60 найдем НОД(100;60)=п 100=2*2*5*5; 60=2*2*5*3;НОД(100;60)=20.Т.е.п=20.Т.е. d=11…11 (20 единиц) 2 способ. Решение. 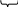 100 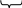 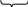 40 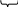 60 11…11=1..1·100…0+11…11 40 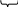 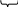 600 600 и НОД(1…1;1…1)= НОД(1…1;1…1)= НОД(1…1;1…1) 100 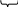 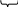 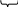 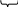 400 400 200 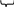 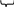 1…1=1…1·100…0+1…1 1…1=1…1·100…0+1…1 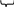 400 200 200 200 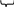 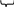 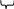 НОД(1…1;1…1)= НОД(1…1;1…1)=1…1 НОД(1…1;1…1)= НОД(1…1;1…1)=1…1200 400 200 200 200 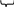 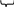 О 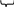 твет:d=1…1(20 единиц) твет:d=1…1(20 единиц)№3 Найдите наибольший общий делитель чисел 12п +13 и n+7 Решение. НОД (2n+13;n +7)= НОД (n+7;n+6)=НОД(n+6;1)=1. Ответ: 1. Задачи на доказательство утверждений. №1 Докажите, что при любом nЄN числа п5+4пЗ+Зп и п4+Зп2+1 взаимно просты
d=1 т.е. НОД(п5+4пЗ+Зп; п4+Зп2+1)=1 №2 Числа k и b -взаимно просты, а их НОК равен 48.Найдите эти числа. Решение: Раскладываем 48 на множители: 1*48;2*24;3*16;4*12;6*8 (затем повторение) Найдем из них взаимно простые: НОД(1 ;48)=1 ,НОД(3; 16)=1 Ответ: k=1, b=48(b=1, k=48) Или k=3, b=16(b=3, k=16) №3 Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты. Доказательство. Пусть НОД(п-1;п)=d, тогда их разность делится на dп-(п-1)=1,а это лишь возможно при d=1т.е. эти числа взаимно просты. №4 Доказать утверждение: «Если пЄNи имеет нечетное количество делителей, то п=q2,qЄN Доказательство. Выпишем делители парами: 1  2:1,12,2,6,3,4., А у квадратов есть и повторная пара: 2:1,12,2,6,3,4., А у квадратов есть и повторная пара:36=1,36,18,2,12,3,6 (6- повторная пара). Значит у квадратов нечётное кол-во делителей. ч.т.д №4 Докажите, что если а-b=2 и числа а и b не являются взаимно простыми, то НОД (а;b)=2 Решение Пусть НОД (а;b)=x, тогда разность (а-b):x т.е. x=1 или x=2. Но т.к а и b взаимно простые, то x=2 ч.т.д Разные задачи. №1 Н  айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998. айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998.Решение. Любой делитель числа 10999 имеет вид с1=2р*5q 0 <р<999. При этом делитель не делит 10 998, если р или qравны 999. Подсчитаем. 1000 штук 2999, 2999 *5,… , 2999*5999 5999 , 5999 *2,…, 5999 *2999 Но можно заметить, что d=29995999 повторяется 2 раза, то всего делителей будет: 1000+1000-1-1999 (шт) Ответ: 1999. №2 Существуют ли такие два натуральных числа а и b,у которых НОД(а;b)=110, а НОК(а;b)=2000; Решение. Не существует, так как для любых натуральных чисел а и b НОД(а;b) является делителем НОК(а;b) Но 110 не является делителем 2000. Ответ: нет №3 Число р-простое. Сколько существует натуральных чисел: Меньших р и взаимно простых с ним. Меньших р2 и взаимно простых с ним. Решение 1) используя, свойство 5 имеем (р-1). 2) Числа р,2р,3р...(р-1)р и р2 не взаимно просты их всего (р-1) шт. А меньших р2 чисел (р2-1). Теперь из р2-1 вычитаем р-1, имеем: р2-1-р+1=р2-р. Ответ: 1) р-1 2) p2-p №4 Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты. Доказательство: Пусть Н0Д(n-1 ;n)=d, тогда их разность делится на dn-(n-1)=1,а это лишь возможно при d=1,т.е. эти числа взаимно просты. Уравнения, содержащие НОК и НОД некоторых чисел. Решить уравнение: 1/x+1/y+1/НОД (х; у)+1/НОК(х; у)=1 Решение: Пусть НОД (х; у)=d, x=d a, y=db НОК(x; y)=d a*db/d=dab НОД (а;b)=1 . Имеем 1/da+1/db+1/d+1/dab=1 | *dab a+b+1+ab=dab а(b+1)+(b+1)=dab (b+1)(a+1)=dab Предположим а≤b: (b+1)(а+1) кратно b (т.к. dab кратно d),а НОД(b+1;b)=1, то (а+1) кратно и а+1=b t Имеем : а+1≤b+1 bt≤b+1 Пусть t= 1, значит а+1=b b+1=da, a+2=da 2=a(d-1) а=1, то d=3 и b=2, х=3,y=6 Одно решение (3;6) Если а=2, то d=2 и b=3 x=4,у=6 другое решение (4;6) 2)Пустьt=2,b=1 а+1=2, а=1, d=4( из уравнения), х=у=4 Другое решение (4;4) t≠3, т.к. bt≤b+1 Зb≤b+1 t<3 2b≤1 (ноbЄN) Других решений нет. Ответ: (3;6);(6;3);(4;6);(6;4);(4;4) №2 Решить уравнение. НОК(а;6)=18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
