Как НОД и НОК помогают решать разнообразные интересные задачи. Как НОК и НОД чисел помогает решать разнообразные интересные зад. Как нок и нод чисел помогает решать интересные и разнообразные задачи

Название	Как нок и нод чисел помогает решать интересные и разнообразные задачи
Анкор	Как НОД и НОК помогают решать разнообразные интересные задачи
Дата	21.04.2023
Размер	173 Kb.
Формат файла
Имя файла	Как НОК и НОД чисел помогает решать разнообразные интересные зад.doc
Тип	Решение #1079879
страница	3 из 3

1 2 3

Решение.

Соответственно, число а имеет вид: а=2*3*3=18; НОД(а;6)=18=2*3*3=18 или следующий: а=3*3=9.

Ответ: а=18 или а=9
№3

Решить уравнение.

НОД (а;8)=4

Решение.

Число а имеет вид: а=2*2*n (n-нечётное) Соответственно отсюда можно найти т.к дополняя множителями делящимися на 2 мы увеличиваем НОД, т.е. значения а-бесконечно.

а=2*2*1=4,

а=2*2*3=12,

а=2*2*5=20 и.т.д

Т.е n=2k-1 (k-натуральное)
№4

Решить уравнение НОД (а;8)=а-10

Решение:

Имеем: аЄN, а>10

НОД (а;8) может быть равен 1,2,4,8

Подставим в уравнение.

1=а-10, а=11

2=а-10, а=12

4=а-10, а=14

8=а-10, а=18,Из них удовлетворяют только а=11

Ответ: а=11

№5

Решить уравнение НОК (а;8)=9а-9

Решение.

НОК (а;8) может быть а,2а,4а,8а.

Подставим:

1)а=9а-9, а=1,125

2)2а=9а-9, а=9/7

3)4а=9а-9,а=1,8

4) 8а=9а-9, а=9

1),2),3) случаи не удовлетворяют а ЄN

Ответ: а=9
№6
Сколько пар натуральных чисел (а;b), где а меньше или равно b удовлетворяет равенству НОК(а;b)=НОД(а;b)+10?
Решение.

Пусть d=НОД(а;b) dделит и а и b следовательно делит и любое кратное чисел аиb ,таким образом из равенства НОК(а;b)=d+10 следует, что d делит 10. Но у числа 10 ровно четыре делителя: 1,2,5,10,следовательно ,никаких других значений d принимать не может. НОК(а;b)=аb\d. Сделаем перебор возможных значений:

если d=1 ,то аb= 11 и получаем пару( 1; 11)
если d=2,то аb=2(2+10)=24, получаем еще две пары (4;6)и (2;12)
если d=5,то аb=5(5+10)=75,получаем пару (5; 15)
если d=10,то аb=10(10+10)=200, получаем пару (10;20).

Ответ: 5 пар.

Решение систем уравнений

№1

Решить систему:

а 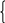+b=288

НОД(а;b)=З6

Решение:

а=36k,b=36п.

Н0Д(k;п)=1, тогда

a+b=288, 36k+36п=288, k+п=8

Подберем все k и n, чтоб k+п=8, Н0Д(k;п)=1

Пары: 7 и 1, 5 и 3.

Отсюда находим а и b: 252,36; 180,108.

Ответ: 252,36; 180,108.

№2

Решить систему:

а 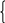:b=5:7

НОК(а;b)=140

Решение:

Выразим: а=5d, Ь=7d

Выразим: НОК(а;b) =аb/d=5d* 7d/d=35d

35d=140

d=4 Отсюда а=20,b=28.

Ответ:(20;28)
№3

Решить систему: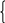

а b=40

НО К(а;b)=20

Решение:

НОД(а;b) =аb:НОК (а;b) =2

а=2k, b=2п;Н0Д(k;п)=1

НОК (а;b)=(2k+2п):2=2kп

2kп=20 ,kп=10 ,Н0Д(k;п)=1

Подберем значения k,п: 1,10;2,5.

Отсюда а и b: 2,20; 4,10.

Ответ: 2,20;4,10.
№4

Решить систему:

а 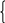-b=60

НОД(а;b)=288

Решение:

а=288k, Ь=288п ,Н0Д(k; п)=1,

288k-288п=60 \:12, 24k-24п=5, k-п=5:24

Что означает: Нет решений

Т.к. kЄN, п ЄN,(k-n)ЄNk>п т.к. а>b

Ответ: Нет решений

№5

Решить систему.

НОК(a; b)=1989;

НОД(a ;b)=13,
Р ешение.

НОК(a;b)=1989;

НОД(a;b)=13,

НОК(a; b)=a b/НОД(a; b)=13xy

a

=13х

b=13y

НОД(x;y)=1

13ху=1989
a

=13х

b=13y

x y =153
153=153*1(отсюда a=13 , b=1989 или a=1989,b=13)

153=9*17( отсюда a=117,b=221или a=221,b=117)

153=3*51,не подходит т.к. НОД(x;y)≠1

Ответ: (13;1989);(1989;13);(117;221);(221;117).
№6

Решите систему:

Н ОД(a;b)=17;

НОК(a;b)=204,

Решение.

НОК(a;b)=аb/НОД(а;b)=17xy

Н ОД(a;b)=17;

НОК(a;b)=204,
a =17x

b=17y

204=17хy

a=17x

b=17y

12=хy
Раскладываем:12:1*12,2*6,3*4 (затем повторение)

НОД(1;12)=1;Тогда a=17,b=204илиb=17,a=204.

НОД(3;4)=1;Тогда a=51,b=68 или a=68,b=51.

Ответ: (17;204);(204;17);(51;68);(68;51).

Графики функций с НОД и НОК.
Рассмотрим простейшую функциюy=НОД(х;1); после нескольких преобразований получим 1= НОД(х;1)

Рассмотрим систему координат с осями на которых отмечены действительные числа. Тогда график будет выглядеть в виде точек. Рассмотрим систему координат с осями в натуральных числах, то график исходной функции выложится в прямую.

у

1 . . . . . . . .

Примечание: для построения графиков

1 2 3 4 5 6 7 8 х функций можно указать 2 рассмотренных

случая, но обязательно во втором указать, что оси содержат только натуральные числа.

Пример 1: Построим график функции у = НОД (х;4)

Эту функцию можно выложить в три случая:

х=2k-1, y=1
x=2(2m-1)=4m-2, y=2
x=4n, y=4

Расставим соответствующим образом точки в системе координат.

у
4 .

3

2 . .
1 . . .

х

1 2 3 4 5 6

Примечание: нужно заметить, что в большинстве случаев графики функций с НОД и НОК получаются периодические.

Правило построения графиков функций с НОК и НОД—это аналитическое рассмотрение случаев и отображение на осях системы координат.

Примечание: конечно перебор случаев для построения сложных графиков очень громоздкое дело, но для простых это срабатывает.
Пример 2:Распишем функцию у = НОК (х;8) на несколько случаев:

х=2k-1 у=8х (kЄN)
x=2(2m-1)=4m-2, у=4х (mЄN)
х=4(2p-1)=8p-4, y=2x (pЄN)
x=8n, y=x (nЄN)

Пример 3: Построим график функции у = НОД(х;8)+НОД(х;2)

Распишем функцию у = НОД (х;8)+НОД(х;2) на несколько случаев:

х=2k-1 у=2 (kЄN)
x=2(2m-1)=4m-2, у=4 (mЄN)
х=4(2p-1)=8p-4, y=6 (pЄN)
x=8n, y=10 (nЄN)

у
10 .

9

8

7

6 .

5

4 . .

3

2 . . . .

1

1 2 3 4 5 6 7 8

Функция у = НОД(х;8)+НОД(х;2)― периодические, поэтому

график построен на отрезке [1;8]

Используемая литература:

1.Н.Я.Виленкин. Алгебра8.(углубленное изучение) М.:Просвещение,1995.

2.В.В.Кривоногов. Нестандартные задания по математике.5-11кл.М: «Первое сентября»,2002.

З.Т.П. Пахтина. Раз задачка, два задачка. М.:Просвещение,2002.

4.А.Р.Рязановский. Дополнительные материалы по курсу математики. М.:Просвещение,2002.

5.М.Я.Выготский. Справочник по элементарной математике.

6. Олимпиадные задачи. Математика в школе . №8,2000.

7 Олимпиадные задачи Газета «Математика»№10,№7,2000.

8.В.Н.Березин. Сборник задач для факультативных занятий по математике.

М.: Просвещение, 1985.

9Л.И.Звавич. Задания для проведения письменного экзамена по

математике.9кл.М.:Просвещение1995.

10.С.М.Никольский. Алгебра 8.М.:Просвещение,2000.

1 2 3