выпуклый многоугольник. Как определить, что данный не самопересекающийся многоугольник выпуклый
 Скачать 40.91 Kb. Скачать 40.91 Kb.
|
|
Как определить, что данный не самопересекающийся многоугольник выпуклый? Выпуклые многоугольники имеют следующие признаки: Многоугольник, который лежит по одну сторону от каждой прямой, проходящая через две его соседние стороны; Сумма внешних углов выпуклого многоугольника равна 360°; Сумма углов выпуклого многоугольника равна (n - 2) * 180°; Все внутренние углы многоугольника меньше 180°; Все диагонали, связывающие вершины многоугольника, лежат внутри этого многоугольника; Все углы многоугольника обходятся в одном направлении (Рисунок 1). 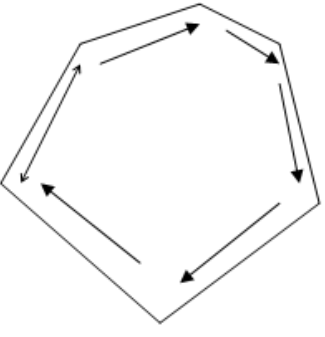 В КГ многоугольник будет выпуклым если при его обходе в каждой тройке последовательных вершин происходит поворот всегда в одну и ту же сторону. При обходе многоугольника против часовой стрелке поворот будет всегда налево, а при обходе по часовой - направо. Многоугольник будет выпуклым, если для векторов, составляющих его периметр, выполняется условие: векторные произведение соседних векторов должны иметь одинаковый знак. В общем случае, произведение векторов в трехмерном пространстве находится по формуле: 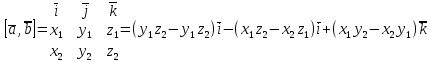 Здесь i, j, k - орты декартовой системы (вектора единичной длины, сонаправленные с осями координат). Однако, если мы рассматриваем вектора, лежащие в одной плоскости, то для этого случая z-составляющая векторов будет нулевой. Тогда наша формула вырождается в: 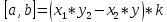 Таким образом, мы должны обойти все пары соседних сторон-векторов и посмотреть, все ли их произведения одного знака. (То есть все ли значения разности произведений (xi*yi+1-xi+1*yi) одного знака для всех i от 1 до N-1). Исходя из этого мы можем составить следующий алгоритм: Задаем N - количество вершин многоугольника Задаем (вводим или присваиваем) все вершины многоугольника Pxi, Pyi для всех i от 1 до N. Полагаем многоугольник выпуклым Q=true. Вычисляем 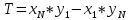 Вычисляем Z=T/|T|, где |T| - модуль числа Т. Полагаем P=1 Для всех i от 1 до N-1 при условии, что Q=true вычисляем: xi,yi xi+1, yi+1 R=xi*yi+1-xi+1*yi P=P*Z*R/|R|, здесь |R| - модуль числа R. если P <0, то Q=false Если Q=true - многоугольник выпуклый, иначе - нет. Вычисление координат вектора, образованного сторонами многоугольника (xi, yi), хорошо производить в отдельной процедуре. xi=Pxi+1-Pxi yi=Pyi+1-Pyi Для N-ой вершины N+1-ая будет, естественно, первой. |
