тренировочка. Какое из уравнений называется дифференциальным уравнением nого порядка
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
| | Определить тип дифференциального уравнения 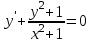 | 1. с разделяющимися переменными 2. линейное I-ого порядка 3. уравнение Бернулли 4. однородное 5. линейное II-ого порядка |
| | Какое из уравнений является уравнением Бернулли? | 1. 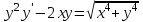 2. 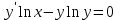 3. 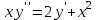 4. 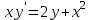 5. 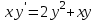 |
| | Укажите правильную формулировку теоремы существования и единственности задачи Коши для дифференциального уравнения n-ого порядка 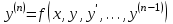 | 1. если в уравнении функции f непрерывна в некоторой области, которая содержит точку 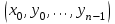 , то существует и притом единственное решение , то существует и притом единственное решение 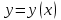 уравнение, удовлетворяющее начальному условию уравнение, удовлетворяющее начальному условию 2. если в уравнении функции f определена в области, которая содержит точку 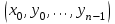 , то существует и притом единственное решение , то существует и притом единственное решение 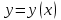 уравнение, удовлетворяющее начальному условию уравнение, удовлетворяющее начальному условию3. если в уравнении частные производные f по всем аргументам непрерывны в области которая содержит точку 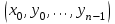 , то существует и притом единственное решение уравнения , то существует и притом единственное решение уравнения4. если в уравнении функции f и её частные производные по аргументам 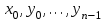 , непрерывны в некоторой области, которая содержит точку , непрерывны в некоторой области, которая содержит точку 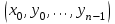 , то существует и притом единственное решение , то существует и притом единственное решение 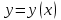 уравнения удовлетворяющего начальному условию уравнения удовлетворяющего начальному условию 5. если в уравнении функция f непрерывна то существует и притом единственное решение этого уравнения |
| | Укажите функцию, которая является общим решением уравнения 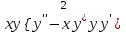 | 1. 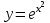 2. 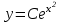 3. 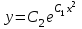 4. 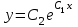 5. 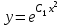 |
| | Какое из уравнений интегрируется с помощью подстановки 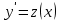 ? ? | 1. 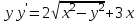 2. 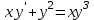 3. 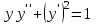 4. 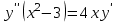 5. 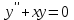 |
| | Какое из уравнений интегрируется с помощью подстановки 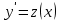 ? Д.б. (y) ? Д.б. (y) | 1. 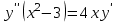 2. 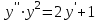 3. 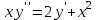 4. 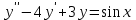 5. 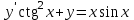 |
| | Какое из уравнений является линейным, неоднородным дифференциальным уравнением n-ого порядка? | 1. 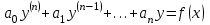 2. 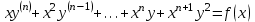 3. 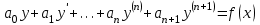 4. 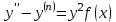 5. 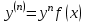 |
| | Какое из уравнений является однородным линейным дифференциальным уравнением n-ого порядка ? | 1. 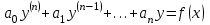 2. 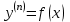 3. 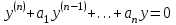 4. 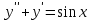 5. 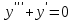 |
| | Какое из уравнений является однородным линейным дифференциальным уравнением n-ого порядка? | 1. 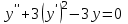 2. 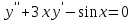 3. 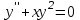 4. 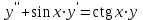 5. 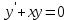 |
| | Если y1 и y2 – частные линейно независимые решения уравнения 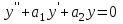 , то какая комбинация из указанных функций также будет решением? , то какая комбинация из указанных функций также будет решением? | 1. 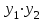 2. 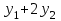 3. 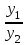 4. 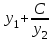 5. 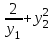 |
| | Если y1 и y2 – частные линейно независимые решения уравнения 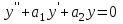 , то какое из следующих выражений является общим решением этого уравнения? , то какое из следующих выражений является общим решением этого уравнения? | 1. 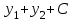 , где , где 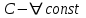 2. 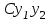 , где , где 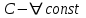 3. 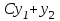 , где , где 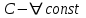 4. 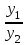 5. 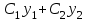 , где , где 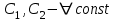 |
| | Указать определитель Вронского дифференциальных функций y1 и y2 | 1. 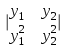 2. 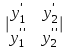 3. 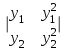 4. 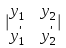 5. 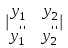 |
| | Определить линейно-независимые функции | 1. 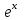 и и 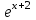 2. 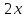 и и 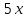 3. 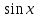 и и 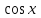 4. 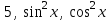 5. 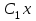 и и 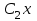 |
| | Если вронскиан 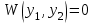 , то функции y1 иy2? , то функции y1 иy2? | 1. линейно независимы 2. 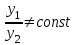 3. 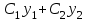 - общее решение уравнения - общее решение уравнения 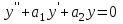 4. 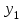 и и 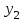 сравнить нельзя сравнить нельзя5. линейно зависимы |
| | Указать формулу Лиувилля | 1. 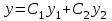 2. 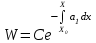 3. 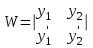 4. 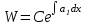 5. 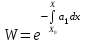 |
| | Если известно одно частное решение y1 уравнения 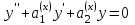 | 1. 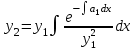 2. 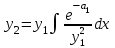 3. 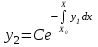 4. 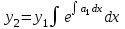 5. 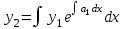 |
| | Пусть 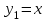 - частное решение уравнения - частное решение уравнения 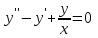 . Найти другое частное решение (используя формулу Лиувилля) . Найти другое частное решение (используя формулу Лиувилля) | 1. 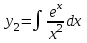 2. 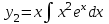 3. 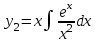 4. 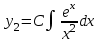 5. 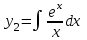 |
| | Определить характеристическое уравнение для дифференциального уравнения n-ого порядка 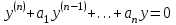 | 1. 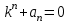 2. 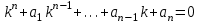 3. 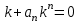 4. 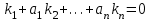 5. 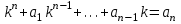 |
| | Какое частное решение соответствует действительному корню с кратностью единицы характеристического уравнения для однородного линейного дифференциального уравнения n-ого порядка? | 1. 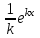 2. 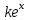 3. 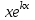 4. 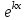 5. 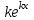 |
| | Какое частное решение соответствует действительному корню с кратностью r характеристического уравнения для однородного линейного дифференциального уравнения II-ого порядка? | r линейно независимых частных решений 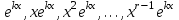 2. линейно независимые решения 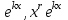 3. 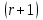 частных решений частных решений 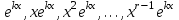 4. 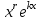 5. 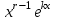 |
| 48. | Какое частное решение соответствует паре комплексно сопряжённых корней 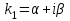 и и 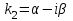 характеристического уравнения для однородного линейного уравнения дифференциального уравнения n-ого порядка? характеристического уравнения для однородного линейного уравнения дифференциального уравнения n-ого порядка? | 1. 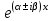 2. 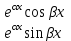 3. 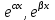 4. 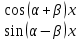 5. 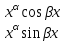 |
| 49. | Какое решение соответствует каждой паре комплексно сопряжённых корней 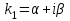 и и 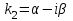 кратности характеристического уравнения для однородного линейного уравнения дифференциального уравнения n-ого порядка? кратности характеристического уравнения для однородного линейного уравнения дифференциального уравнения n-ого порядка? | 1. 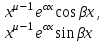 2. 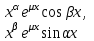 3. 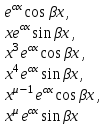 4. 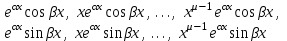 5. 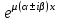 |
| 50. | Указать частное решение для линейного однородного дифференциального уравнения II-ого порядка | 1. 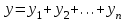 , где , где 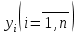 - линейно независимые решения дифференциального уравнения n-ого порядка - линейно независимые решения дифференциального уравнения n-ого порядка2. 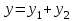 , где , где 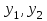 - линейно независимые решения уравнения - линейно независимые решения уравнения 3. 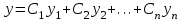 , где , где 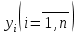 - линейно независимые решения уравнения - линейно независимые решения уравнения |
