|
Какое из уравнений называется дифференциальным уравнением n-ого порядка.
|
1.
2.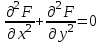
3. 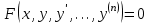
4.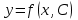
5.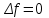
|
|
Определите порядок дифференциального уравнения 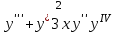 . .
|
1. 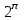
2. 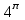
3. 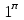
4. 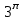
5. 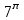
|
|
Что называется порядком дифференциального уравнения
|
1. n-ый порядок производной
2. наибольшая производная функции
3. порядок производной от неизвестной функции, входящей в уравнение
4. наибольший порядок производной от неизвестной функции, входящей в уравнение
5. степень производной функции, входящей в уравнение
|
|
Какая функция является решением дифференциального уравнения?
|
1. всякая функция, которая при подстановке в дифференциальное уравнение обращает его в тождество
2. любая функция
3.
4. непрерывная функция
5. интегрируемая функция
|
|
Указать общее решение дифференциального уравнения 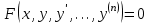
|
1. 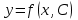
2. 
3. 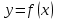
4. 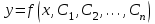
5. 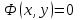
|
|
Указать общий интеграл дифференциального уравнения 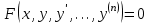
|
1. 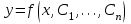
2. 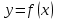
3. 
4. 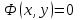
5. 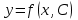
|
|
Указать постановку задачи Коши для дифференциального уравнения n-ого порядка
|
1. 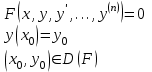
2. 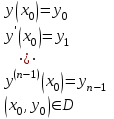
3. 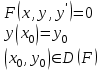
4. 
5. 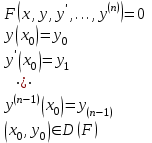
|
|
Какая из заданных функций является общим решением уравнения 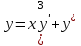
|
1. 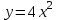
2. 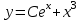
3. 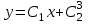
4. 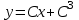
5. 
|
|
Какая из функций является решением задачи Коши 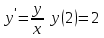
|
1. 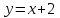
2. 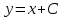
3. 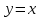
4. 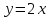
5. 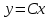
|
|
Определите задачу Коши для дифференциального уравнения I-ого порядка
|
1. 
2. 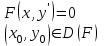
3. 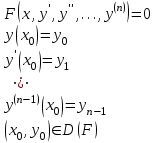
4. 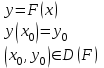
5. 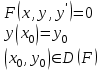
|
|
Определите задачу коши для дифференциального уравнения II-ого порядка
|
1. 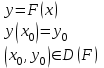
2. 
3. 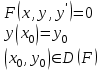
4. 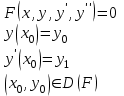
5. 
|
|
Всегда ли дифференциальное уравнение I-ого порядка имеет вид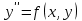 ? ?
|
1. всегда
2. иногда
3. когда уравнение 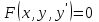 разрешимо относительно у разрешимо относительно у
4. чаще всего
5. никогда
|
|
Геометрический смысл дифференциального уравнения 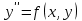
|
1. это тангенс угла наклона касательной к кривой
2. семейство интегральных кривых, в каждой точке которых заданна касательная к ней 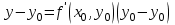
3. это кривая, в каждой точке которой известна касательная к ней
4. система интегральных кривых с касательной 
5. совокупность всех кривых с заданным углом наклона
|
|
Определить дифференциальное уравнение с разделяющимися переменными
|
1. 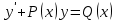
2. 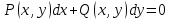
3. 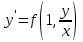
4. 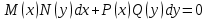
5. 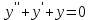
|
|
Укажите точную формулировку теоремы задачи о существовании и единственности (задачи Коши)
|
1. через все точки 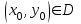 проходит одна и только одна интегральная кривая уравнения проходит одна и только одна интегральная кривая уравнения 
2. если 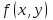 в уравнении в уравнении  определена в некоторой D, то через все точки определена в некоторой D, то через все точки 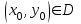 проходит одна и только одна интегральная кривая этого уравнения проходит одна и только одна интегральная кривая этого уравнения
3. пусть функция 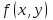 в уравнении в уравнении  и её частная производная и её частная производная 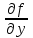 непрерывны в области D, содержащей точку непрерывны в области D, содержащей точку 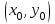 , тогда существует единственное решение , тогда существует единственное решение 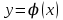 , удовлетворяющее н.у. , удовлетворяющее н.у. 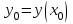
4. решение задачи Коши заполняет всю область D
5. пусть функция 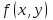 в уравнении в уравнении  и её частная производная и её частная производная 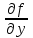 непрерывны в области D, тогда существует единственно верное решение непрерывны в области D, тогда существует единственно верное решение 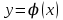
|
|
Какое из уравнений является дифференциальным уравнением с разделяющимися переменными?
|
1. 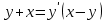
2. 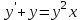
3. 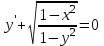
4. 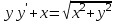
5. 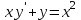
|
|
Какая из функция является однородной?
|
1. 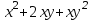
2. 
3. 
4. 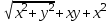
5. 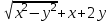
|
|
Каков порядок однородной функции 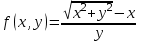 ? ?
|
1. 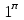
2. 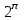
3. не является однородной
4. 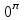
5. 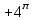
|
|
Какое из уравнений I-ого порядка является однородным?
|
1. 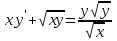
2. 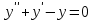
3. 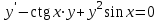
4. 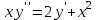
5. 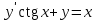
|
|
Какое из уравнений I-ого порядка интегрируется с помощью замены  ? ?
|
1. линейное
2. уравнение Бернулли
3. однородное
4. с разделяющимися переменными
5. ни одного из известных дифференциальных уравнений I-ого порядка
|
|
Указать общий вид линейного дифференциального уравнения I порядка
|
1. 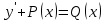
2. 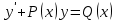
3. 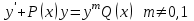
4. 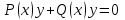
5. 
|
|
Какое из уравнений является линейным I-ого порядка?
|
1. 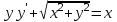
2. 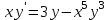
3. 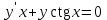
4. 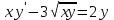 ? ?
5. 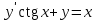
|
|
Решением какого уравнения является следующая формула: 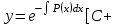
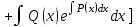 ? ?
|
1. однородное
2. уравнение Бернулли
3. с разделяющимися переменными
4. линейного I-ого порядка
5. линейного II-ого порядка
|
|
Каким методом ищется решение линейного дифференциального уравнения I-ого порядка?
|
1. подстановкой  ? ?
2. методом Бернулли 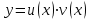
3. заменой 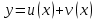
4. заменой 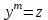
5. заменой 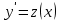
|
|
Какое уравнение интегрируется с помощью подстановки 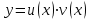 ? ?
|
1. 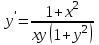
2. 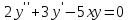
3. 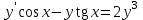
4. 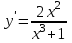
5. 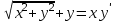
|
|
Какое из уравнений называется уравнением Бернулли?
|
1. 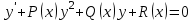
2. 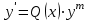
3. 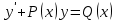
4. 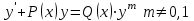
5. 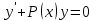
|
|
Какое из уравнений интегрируется с помощью подстановки 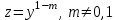 ? ?
|
1. 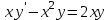
2. 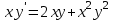
3. 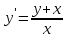
4. 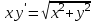
5. 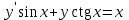
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.