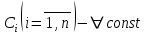
4. 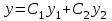 , где
, где 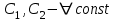 ,
, 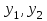 - линейно независимые решения уравнения
- линейно независимые решения уравнения
5. 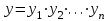 , где
, где 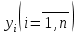 - линейно независимые решения уравнения
- линейно независимые решения уравнения
51.
|
Указать характеристическое уравнение для линейного однородного дифференциального уравнения II-ого порядка 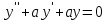
|
1. 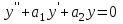
2. 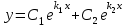
3. 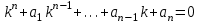
4. 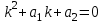
5. 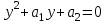 , где y – решение уравнения , где y – решение уравнения
|
52.
|
Укажите общее решение линейного однородного дифференциального уравнения II-ого порядка в случае действительных и различных 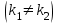 корней характеристического уравнения корней характеристического уравнения
|
1. 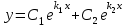 , где , где 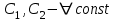
2. 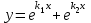
3. 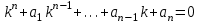
4. 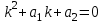
5. 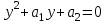 - где y – решение уравнения - где y – решение уравнения
|
53.
|
Определить общее решение линейного однородного дифференциального уравнения II-ого порядка в случае действительных и равных 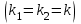 корней характеристического уравнения корней характеристического уравнения
|
1. 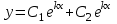 , где , где 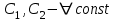
2. 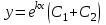 , где , где 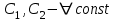
3. 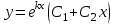 , где , где 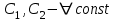
4. 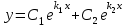 , где , где 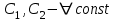
5. 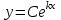 , где , где 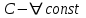
|
54.
|
Определить общее решение линейного однородного дифференциального уравнения II-ого порядка в случае комплексно сопряжённых 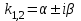 корней характеристического уравнения корней характеристического уравнения
|
1. 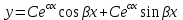 , где , где 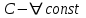
2. 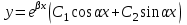 , где , где 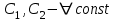
3. 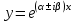
4. 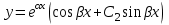
5. 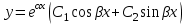 , где , где 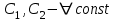
|
55.
|
Указать формулировку для общего решения неоднородного линейного дифференциального уравнения n-ого порядка, если yr – частное решение уравнения , а y0 – общее решение соответствующего однородного линейного дифференциального уравнения n-ого порядка
|
1. 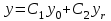 , где , где 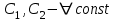
2. 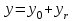
3. 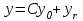 , где , где 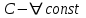
4. 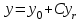 , где , где 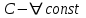
5. 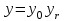
|
56.
|
Если правая часть линейного неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид, то в каком случае частное решение находится только методом Лагранжа?
|
1. 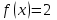
2. 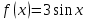
3. 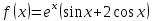
4. 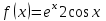
5. 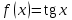
|
57.
|
При каком виде правой части неоднородного дифференциального уравнения с постоянными коэффициентами частное решение можно строить методом подбора?
|
1. 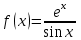
2. 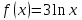
3. 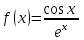
4. 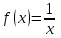
5. 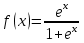
|
58.
|
Определить общее решение уравнения 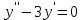
|
1. 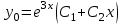 , где , где 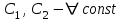
2. 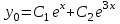 , где , где 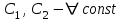
3. 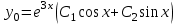 , где , где 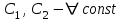
4. 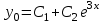 , где , где 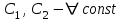
5. 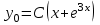 , где , где 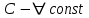
|
59.
|
Какое из уравнений является линейным неоднородным дифференциальным уравнением II-ого порядка?
|
1. 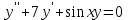
2. 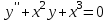
3. 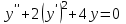
4. 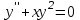
5. 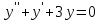
|
60.
|
Определить функцию, являющуюся частным решением уравнения 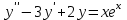
|
1. 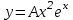
2. 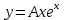
3. 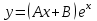
4. 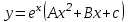
5. 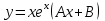
|
61.
|
Какое уравнение интегрируется только методом вариации произвольных постоянных?
|
1. 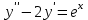
2. 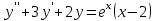
3. 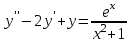
4. 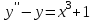
5. 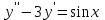
|
62.
|
Какое из уравнений является линейным неоднородным дифференциальным уравнением II-ого порядка с постоянными коэффициентами?
|
1. 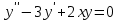
2. 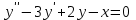
3. 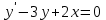
4. 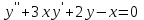
5. 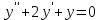
|
63.
|
Указать общее решение уравнения 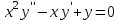 , если известны два его частных решения , если известны два его частных решения 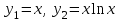
|
1. 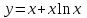
2. 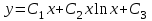
3. 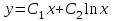
4. 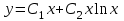
5. 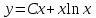
|
64.
|
Какое из уравнений может интегрироваться методом подбора частного решения?
|
1. 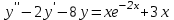
2. 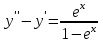
3. 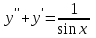
4. 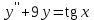
5. 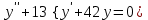
|
65.
|
Какие две данные функции линейно зависимы?
|
1. 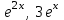
2. 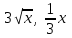
3. 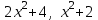
4. 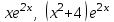
5. 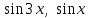
|
66.
|
Какое из уравнений является линейным однородным III-его порядка?
|
1. 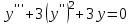
2. 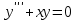
3. 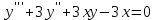
4. 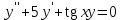
5. 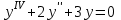
|
67.
|
Дано общее решение однородного уравнения 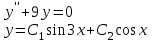 укажите систему для нахождения общего решения неоднородного уравнения укажите систему для нахождения общего решения неоднородного уравнения 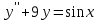 по методу Лагранжа по методу Лагранжа
|
1. 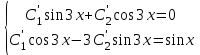
2. 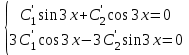
3. 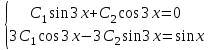
4. 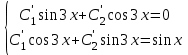
5. 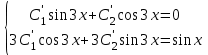
|
68.
|
Какой вид должны иметь правая часть неоднородного линейного дифференциального уравнения с постоянными коэффициентами, чтобы его частное решение строилось методом подбора?
|
1. 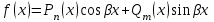
2. 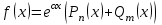
3. 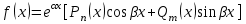
4. 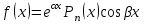
5. 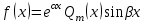
|
69.
|
В каком виде ищется частное решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами со специальной правой частью?
|
1. 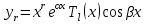
2. 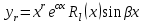
3. 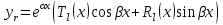
4. 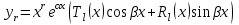
5. 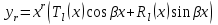
|
70.
|
Чему равно r в формуле 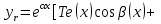 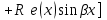 , если , если 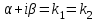 (корни характеристического уравнения) для неоднородного линейного дифференциального уравнения II-ого порядка с постоянными коэффициентами со специальной правой частью? (корни характеристического уравнения) для неоднородного линейного дифференциального уравнения II-ого порядка с постоянными коэффициентами со специальной правой частью?
|
1. 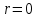
2. 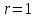
3. 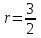
4. 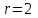
5. 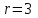
|
71.
|
Чему равно r в формуле 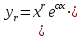 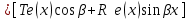 если если 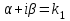 или или 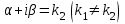 - (k1k2 - корни характеристического уравнения ) для неоднородного линейного дифференциального уравнения II порядка с постоянными коэффициентами со специальной правой частью? - (k1k2 - корни характеристического уравнения ) для неоднородного линейного дифференциального уравнения II порядка с постоянными коэффициентами со специальной правой частью?
|
1. 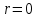
2. 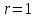
3. 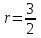
4. 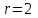
5. 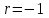
|
72.
|
Чему равно r в формуле 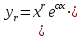 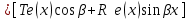 если если 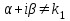 или или 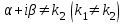 - (k1, k2 - корни характеристического уравнения ) для неоднородного линейного дифференциального уравнения II порядка с постоянными коэффициентами со специальной правой частью? - (k1, k2 - корни характеристического уравнения ) для неоднородного линейного дифференциального уравнения II порядка с постоянными коэффициентами со специальной правой частью?
|
1. 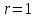
2. 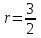
3. 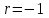
4. 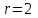
5. 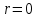
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.