картография. реферат картография ира. Картографические проекции. Карты для начальной школы
 Скачать 319.51 Kb. Скачать 319.51 Kb.
|
 Государственное автономное образовательное учреждение профессионального образования города Севастополя «Институт развития образования» (ГАУО ПО ИРО) РЕФЕРАТ на тему: «Картографические проекции. Карты для начальной школы.» Учебная дисциплина, МДК: 01.05 Естествознание с методикой преподавания Специальность: 44.02.02 Преподавание в начальных классах Руководитель:  (Ф.И.О.) Шевчук О.А.  (Ф.И.О.) Студентка группы НК-21-1з Анишина И.Ю. «20» марта 2022 г Севастополь 2022 СОДЕРЖАНИЕ Введение………………………………………………………………….3 1.Понятие о картографических проекциях…………………………...4-8 2.Классификация проекций по виду меридианов и параллелей нормальной сетки……………………………………………………...9-15 3.Карты для начальной школы………………………………………16-18 Заключение……………………………………………………………...19 Список литературы……………………………………………………..20 Введение Подобно многим отраслям знания научные истоки современной картографии и географии берут начало в античной Греции. Греки установили шарообразность Земли и вычислили ее размеры. Им принадлежат первые картографические проекции и введение в научный обиход меридианов и параллелей. Они являются создателями географических карт в. строго научном понимании этого термина. Развитию в Греции географических знаний способствовало колонизационное движение. Оно привело к образованию греческих колоний на обширном пространстве от восточного побережья Пиренейского полуострова до северных берегов Черного моря. Эти колонии распространились почти на весь известный грекам мир. Дальнейшему накоплению географических знаний содействовали походы Александра Македонского. (334 - 323 гг. до н.э), сопровождавшиеся крупными географическими открытиями. Понятие о картографических проекциях. Классификация проекций по характеру искажений При переходе от физической поверхности Земли к ее отображению на плоскости (на карте) выполняют две операции: проектирование земной поверхности с ее сложным рельефом на поверхность земного эллипсоида, размеры которого установлены посредством геодезических и астрономических измерений, и изображение поверхности эллипсоида на плоскости посредством одной из картографических проекций. Картографическая проекция - математически определенный способ отображения поверхности эллипсоида на плоскости устанавливает аналитическую зависимость (соответствие) между географическими координатами, точек земного эллипсоида и прямоугольными координатами тех же точек на плоскости. Эта зависимость может быть выражена двумя уравнениями вида: х=f1(В,L), у=f2(В, L) (1), называемыми уравнениями картографических проекций. Они позволяют вычислять прямоугольные координаты х, у изображаемой точки по географическим координатам В и L. .Число возможных функциональных зависимостей и, следовательно, проекций неограниченно. Необходимо лишь, чтобы каждая точка B, L эллипсоида изображалась на плоскости однозначно соответствующей точкой х, у и чтобы изображение было непрерывным. Поверхность эллипсоида (или шара) нельзя развернуть на плоскости подобно поверхности конуса или цилиндра. Поэтому непрерывность и однозначность изображения достигаются как бы за счет неравномерного растяжения (или сжатия), т. е. деформации поверхности эллипсоида при совмещении ее с плоскостью. Отсюда следует, что масштаб плоского изображения не может быть постоянным. Для наглядного представления о величине и характере деформаций, свойственных определенной проекции, рассматривают, как изображаются на плоскости бесконечно малые окружности, взятые в разных точках на поверхности эллипсоида. В теории картографических проекций доказывается, что бесконечно малая окружность на поверхности эллипсоида в общем случае изображается на плоскости эллипсом, называемым эллипсом искажений. Это означает, что масштаб изображения зависит не только от положения точки, но может изменяться в данной точке с переменой направления. Различают главный масштаб, равный, масштабу модели земного эллипсоида, уменьшенного в заданном отношении для изображения на плоскости, и прочие масштабы, называемые частными. Частный масштаб определяется как отношение бесконечно малого отрезка d µ= В любой точке на поверхности эллипсоида имеются два взаимно перпендикулярных направления (называемых главными), которые в проекции также изображаются взаимно перпендикулярными линиями, совпадающими с большой и малой осями эллипса искажения (рис. 1). Очевидно, в эллипсе искажений наибольший масштаб совпадает с направлением большой оси эллипса, а наименьший - с направлением малой оси. Эти масштабы по главным направлениям, выраженные в отношении к главному масштабу, обозначают соответственно через а и б. Вообще говоря, главные направления могут элементы не совпадать с меридианами и параллелями (и их изображением в проекции). В таком случае масштабы по меридиану и параллели обозначают соответственно через m и n.  Рис. 1. Эллипс искажений и его элементы. Непостоянство масштабов в данной точке по разным направлениям можно видеть на рис. 2.6, где длины изображаемых меридианов равны длинам меридианов эллипсоида (разумеется, с уменьшением до масштаба карты), а длины параллелей увеличиваются по мере удаления от экватора. На рисунке отрезки параллелей между двумя меридианами одинаковы на любой широте, тогда как в действительности они уменьшаются с приближением к полюсу до нуля. Таким образом, масштаб вдоль меридианов постоянен в любой точке карты, но вдоль параллелей он возрастает с увеличением широты. Это видно по эллипсам искажений, показанным на рис. 2. 6. Наряду с искажениями длин различают искажения площадей и углов. За искажение площади в некоторой точке карты принимают отношение площади эллипса искажений dP/ к площади dP соответствующего бесконечно малого крута на эллипсоиде, обозначаемое через р:  Рис. 2. Картографические сетки в цилиндрических проекциях: а – равновеликой; б – равнопромежуточной; в – равноугольной. Искажением угла называют разность между углом, образованным двумя линиями на эллипсоиде, и изображением этого угла на карте. Величина искажения углов в данной точке характеризуется наибольшим значением этой разности. Проекций, совершенно лишенных искажений длин, не существует. Такие проекции сохраняли бы подобие и пропорциональность всех частей земной поверхности, что может иметь место только на модели эллипсоида. Вместе с тем есть проекции, свободные от искажения углов или от искажений площадей. Проекции, которые передают величину углов без искажения, называются равноугольными. Одна из них изображена на рис. 2.в. В каждой точке равноугольной проекции масштаб одинаков на всех направлениях (эллипс искажении превращается в окружность) но меняется от точки к точке. Это видно по изменению размеров окружностей - эллипсов искажений. Равновеликие проекции сохраняют площади (эллипсы искажений везде имеют одинаковую площадь) но сильно нарушают подобие фигур (вытянутость эллипсов искажений различна) (см. рис. 2.а). Существует множество проекций, которые не являются ни равноугольными, ни равновеликими, - их называют произвольными. Но нет и не может, быть проекции, которая была бы одновременно равноугольной и равновеликой. Вообще говоря, чем больше искажения углов, тем меньше искажения площадей и, наоборот, среди произвольных проекций выделяют равнопромежуточные, во всех точках которых масштаб по одному из главных направлении постоянен и равен главному масштабу (например, по меридианам или параллелям в проекциях, где они совпадают с главными направлениями) По своим свойствам произвольные проекции лежат между равноугольными и равновеликими. Характер искажений, присущий проекции (равноугольная, равновеликая, равнопромежуточная), отмечается в ее названии. Классификация проекций по виду меридианов и параллелей нормальной сетки В картографической практике распространена классификация проекции по виду вспомогательной геометрической поверхности, которая может быть использована при их построении. С этой точки зрения выделяют проекции: цилиндрические, когда вспомогательной поверхностью служит боковая поверхность цилиндра, касательного к эллипсоиду, или секущего эллипсоид; конические, когда вспомогательной плоскостью является боковая поверхность касательного или секущего конуса; азимутальные, когда вспомогательная поверхность - касательная или секущая плоскость. Геометрическое построение названных проекций отличается большой наглядностью. Для простоты рассуждения вместо эллипсоида воспользуемся шаром. Заключим шар в цилиндр, касательный по экватору (рис. 3.а). Продолжим плоскости меридианов ПА, ПБ, ПВ, ...и примем пересечения этих плоскостей с боковой поверхностью цилиндра за изображение на ней меридианов. Если разрезать боковую поверхность цилиндра по образующей аАа1 и развернуть ее на плоскость, то меридианы изобразятся параллельными равноотстоящими прямыми линиями aAa1, 6Бб1, вВв1, ..., перпендикулярными экватору АБВ... Изображение параллелей может быть получено различными способами. Один из них - продолжение плоскостей параллелей до пересечения с поверхностью цилиндра, что даст в развертке второе семейство параллельных прямых линий, перпендикулярных меридианам. Полученная цилиндрическая проекция (рис. 3. 6) оказывается равновеликой, так как боковая поверхность S шарового пояса АЕДГ, равная 2лRh (где h - расстояние между плоскостями АГ и ЕД), соответствует площади изображения этого пояса в развертке. Главный масштаб сохраняется вдоль экватора; частные масштабы по параллели увеличиваются, а по меридианам уменьшаются по вере удаления от экватора.  Рис. 3. Построение картографической сетки в равновеликой цилиндрической проекции. Другой способ определения положения параллелей основан на сохранении длин меридианов, т. е. на сохранении главного масштаба вдоль всех меридианов. В этом случае цилиндрическая проекция равнопромежуточная по меридианам (см. рис. 2. 6). Для равноугольной цилиндрической проекции необходимо в любой точке постоянство масштаба по всем направлениям, что требует увеличения масштаба вдоль меридианов по мере удаления от экватора в соответствии с увеличением масштабов вдоль параллелей на соответствующих широтах (см. рис. 2. в). Нередко вместо касательного цилиндра используют цилиндр, секущий шар по двум параллелям (рис. 4), вдоль которых при развертке сохраняется главный масштаб. В этом случае частные масштабы вдоль всех параллелей между параллелями сечения будут меньше, а на остальных параллелях - больше главного масштаба. Для построения конической проекции заключим шар в конус, касающийся шара по параллели АБВГ (рис. 5, а). Аналогично предыдущему построению продолжим плоскости меридианов ПА, ПБ, ПВ, ... и примем их пересечения с боковой поверхностью конуса за изображение на ней меридианов. После развертки боковой поверхности конуса на плоскости (рис. 5, 6) меридианы изобразятся радиальными прямыми ТА, ТБ, ТВ, ..., исходящими из точки Т, причем углы между ними будут пропорциональны (но не равны) разностям долгот. Вдоль параллели касания АБВ (дуги окружности радиусом ТА) сохраняется главный масштаб. Положение других параллелей, изображающихся дугами концентрических окружностей, можно определить из разных условий, одно из которых - сохранение главного масштаба вдоль меридианов (АЕ=Ае) - приводит к конической равнопромежуточной проекции. Для построения азимутальной проекции воспользуемся. плоскостью, касательной к шару в точке полюса П (рис. 6). Пересечения плоскостей меридианов с касательной плоскостью дают изображение меридианов Па, Пб, Пв, ... в виде прямых, углы между которыми равны разностям долгот. Параллели, являющиеся концентрическими окружностями, могут быть определены различным путем, например, проведены радиусами, равными выпрямленным дугам меридианов от полюca до соответствующей параллели ПА=Па. Такая проекция равнопромежуточная по меридианам и сохраняет вдоль них главный масштаб. Например, эта проекция использована на эмблеме ООН (рис. 7).  Рис. 4. Цилиндр, секущий шар по двум параллелям. Рис. 5. Построение сетки в равнопромежуточной конической проекции. 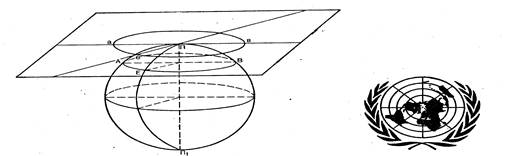 Рис. 6. Построение картографической сетки в азимутальной проекции. Рис. 7. Эмблема ООН - равнопромежуточная азимутальная проекция. 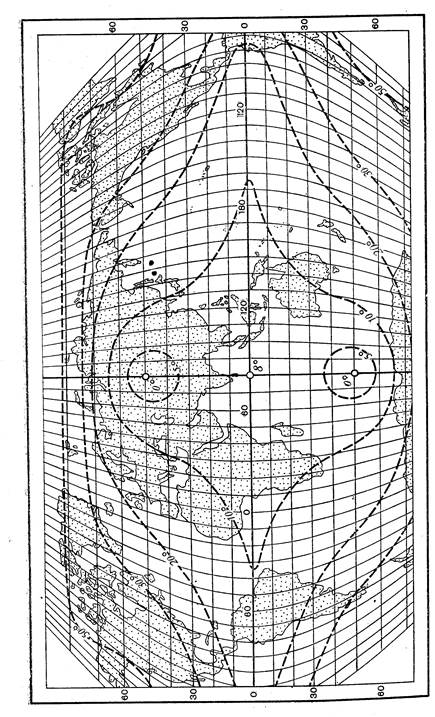 Рис. 8. Картографическая сетка в одной из псевдоцилиндрических проекций (с изоколами углов). Проекции, при построении которых оси цилиндра и конуса совмещались с полярной осью земного шара, а плоскость размещалась касательно в точке полюса, называются нормальными. По виду нормальной сетки различают также проёкции: псевдоцилиндрические, у которых параллели прямые, параллельные друг другу, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана (рис. 8); псевдоконические, где параллели - дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана (рис. 9); поликонические параллели, которых дуги эксцентрических окружностей с центрами на среднем прямолинейном меридиане, а меридианы - кривые, симметричные относительно среднего меридиана (рис. 10). 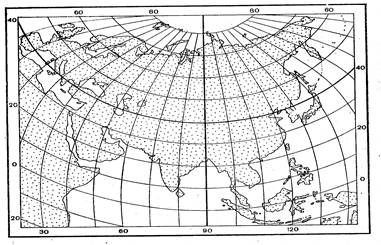 Рис. 9. Картографическая сетка в одной из псевдоконических проекций. 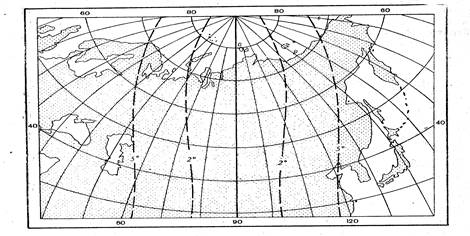 Рис. 10. Картографическая сетка в одной из поликонических проекций (с изоколами углов). Наряду с нормальными сетками в картографии широко используют для цилиндрических и. азимутальных проекций другие ориентировки цилиндра и плоскости: поперечные, когда ось цилиндра лежит в плоскости экватора (рис. 11, а), а плоскость касается шара в одной из точек экватора; косые, когда ось цилиндра (рис. 11, б) образует с полярной осью острый угол, а плоскость касается шара в какой-либо точке между полюсом и экватором. 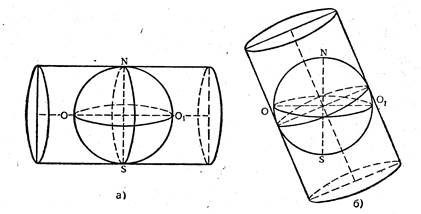 Рис. 11. Положение цилиндра при поперечной (а) и косой (б) цилиндрических проекциях. Карты для начальной школы. Географическая карта – уменьшенное изображение земной поверхности на плоскости условными знаками Особенность географических карт для начальной школы – это, прежде всего, иная проекция карт – по внешнему виду она напоминает часть карты полушарий. Все меридианы сходятся в точке Северного полюса, изображенной на карте. Территория России показана до полюса, чего нет на других картах. Это дает возможность ясно показать детям самую северную точку России на материке – мыс Челюскин на п-ове Таймыр. Северо-восточная и Северо-западная части России показаны не загибающимися вверх по карте, а вытянутыми. Черное море дано полностью в удобном для работы виде. Европейская часть размещена так, что по ней легко работать. К сожалению, при этом происходит увеличение площади России на севере и некоторое уменьшение на юге, что мешает измерению больших расстояний по карте. Изображение линейного масштаба карты представлено именованным и графическим способами, а числового нет. Сейчас в современных атласах дается и этот способ, но учителя не могут использовать его из-за недостаточных математических знаний учащихся начальной школы. Более яркая окраска карты в целом и объемная окраска гор привлекают внимание детей и создают лучшую читаемость карты. Нагрузка географической карты определяется требованиями программы (УМК) или ее назначением, поэтому проводится генерализация, то есть указываются только основные географические объекты характерные для данной территории. Задачи работы с географической картой в начальной школе: научить младших школьников понимать, знать, читать географическую карту. Понимать – означает усвоить главные свойства географической карты, определяющие ее сущность (условность и абстрактность). Это понимание сущности и необходимости масштаба, условных знаков, элементов, указывающих на стороны горизонта, т. е. основных ориентиров карты (полюсов и экватора). Знать географическую карту – это знать ее содержание, определенный минимум названий географических объектов, знать по памяти как размещаются суша и вода, горы и равнины и т. д., помнить и ясно представлять по памяти местоположение объектов, их относительные размеры и форму. Читать географическую карту означает переводить условные знаки карты в словесное описание местности, т. е. видеть местность такой, какой она есть на самом деле. Подготовительный этап ознакомления младших школьников с географической картой начинается с первого класса и включает измерение расстояний на местности, на листе бумаги; развитие пространственных представлений: «далеко», «близко»; определение направлений движения: «вперед», «назад», «вправо», «налево»; ориентирование в своей местности (где находится школа, дом и др. значимые объекты, маршрут движения в школу). На бумаге надо давать упражнения на узнавание направления, затем на воспроизведение и на творческое применение полученных знаний. В третьем классе идет расширение пространственных представлений учащихся, формируются понятия: «горизонт», «линия горизонта», «стороны горизонта» (может проводиться практическая работа на местности с компасом), «ориентирование», способы ориентирования, являющиеся подготовительной работой к изучению плана местности и географической карты. К сожалению, в большинстве УМК по предмету «Окружающий мир» изучение плана местности теперь не предусматривается, а предлагается сразу же изучение географической карты, это в значительной степени затрудняет успешное ее восприятие младшими школьниками, так как нарушается последовательность и постепенность усвоения картографической наглядности. Работа по введению географической карты проводится последовательно и постепенно: условные знаки, масштаб, ориентированность, с использованием физической карты полушарий и физической карты России. Позднее учащихся знакомят с картой «Природные зоны России» и некоторыми другими («Охрана природы», «Экономика России», «Океаны Земли», «Климат Земли» и др.). На уроках в начальной школе можно использовать общегеографические, тематические, контурные карты, а также такие типы карт, как аналитические, синтетические, комплексные, топографические. В процессе обучения учитель формирует у обучающихся умения работать с различными видами карт. Формировать географические знания и умения, географическую культуру ребенка можно, используя следующие типы географических карт: 1. Карта климатических поясов России. 2. План пришкольного участка. Карта города, поселка, села: обучающиеся знают условные знаки плана и карты; отличие плана от карты, их достоинства и недостатки. Умеют начертить план небольшого участка местности, определять по условным знакам изображения объектов на карте. 3. Физическая карта Восточно-Европейской равнины. знают формы рельефа поверхности своего региона; цвет на карте, определяющий равнины и возвышенности. Умеют находить на карте равнины и возвышенности, различать их по типам и описанию, правильно их называть и показывать. 4. Карта месторождений полезных ископаемых. 5.Физическая карта России. Контурная карта России, региона: обучающиеся знают крупные реки и озера нашей Родины, моря, омывающие ее границы, крупные реки и озера своего региона. Показывают моря, реки и озера на физической карте России. 6. Почвенная карта России. 7. Карта природных зон России. Карта животного мира России. 8. Карта полушарий. Контурная карта полушарий: обучающиеся знают местоположение материков и океанов на карте полушарий относительно друг друга, цвета, обозначающие на карте материки и океаны. Работа с географическими картами расширяет кругозор детей, они учатся анализировать свои наблюдения, сопоставлять факты, обобщать, выявлять причинно-следственные связи. Заключение Значение картографической наглядности в развитии младшего школьника велико. Работа с географической картой заменяет учащимся непосредственное изучение территорий земного шара. Она помогает воссоздать их образ, при этом развивается пространственное воображение и пространственные представления детей. Развивается также логическое мышление младшего школьника, т. к. помогает устанавливать связи, анализировать и сравнивать, синтезировать и обобщать. Навыки, приобретаемые учащимися при работе с картой наряду с навыками письма, чтения, счета, относятся к жизненным навыкам и являются неотъемлемой частью начального образования. Список литературы 1. Салищев К.А. Картоведение, 2-е изд. М., Изд-во МГУ, 1982 г. С ил., 408 с. 2. Королев Ю.К. Общая геоинформатика. Ч.1. Теоретическая геоинформатика. – М., 1998.-118 с. 3. Лебедева О.А. Картографические проекции. – Новосибирск, 2000.-35 с. 4. Цветков В.Я. геоинформационные системы и технологии. –М., 1998.-287 с. |
