Картоведение - Салищев. Картоведение вводный и вместе с тем профилирующий курс для студентов, специализирующихся по картографии. В нем излагаются теоретические основы картографической науки
 Скачать 41.52 Mb. Скачать 41.52 Mb.
|
|
Глава 2. Математическая основа карт § 2.1 Понятие о картографических проекциях. Классификация проекций по характеру искажений При переходе от физической поверхности Земли к ее отображению на плоскости (на карте) выполняют две операции: проектирование земной поверхности с ее сложным рельефом на поверхность земного эллипсоида, размеры которого установлены посредством геодезических и астрономических измерений, и изображение поверхности эллипсоида на плоскости посредством одной из картографических проекций. Картографическая проекция - математически определенный способ отображения поверхности эллипсоида на плоскости - устанавливает однозначное соответствие между точками земного эллипсоида и изображениями тех же точек на плоскости. Обычно это соответствие выражают в аналитической форме в двух уравнениях вида (2.1) называемых уравнениями картографических проекций. Они позволяют вычислять прямоугольные координаты х, у изображаемой точки по географическим координатам В и L. Число возможных функциональных зависимостей и, следовательно, проекций неограниченно. Необходимо лишь, чтобы каждая точка В, L эллипсоида изображалась на плоскости однозначно соответствующей точкой х, у и чтобы изображение было непрерывным. Поверхность эллипсоида (или шара) нельзя развернуть на плоскости подобно поверхности конуса или цилиндра. Поэтому непрерывность и однозначность изображения достигаются как бы за счет неравномерного растяжения (или сжатия), т. е. деформации поверхности эллипсоида при совмещении ее с плоскостью. Отсюда следует, что масштаб плоского изображения не может быть постоянным. Для наглядного представления о величине и характере деформаций, свойственных определенной проекции, рассматривают, как изображаются на плоскости бесконечно малые окружности, взятые в разных точках на поверхности эллипсоида. В теории картографических проекций доказывается, что бесконечно малая окружность на поверхности эллипсоида в общем случае изображается на плоскости эллипсом, называемым эллипсом искажений. Это означает, что масштаб изображения зависит не только от положения точки, но может изменяться в данной точке с переменой направления. Эллипс искажений характеризует для этой точки величины искажений длин, площадей и углов. Различают главный масштаб dS, равный масштабу модели земного эллипсоида, уменьшенного в заданном отношении для изображения на плоскости, и прочие масштабы, называемые частными. Частный масштаб dS,определяется как отношение бесконечно малого отрезка на карте (на плоскости) к соответствующему ему отрезку на поверхности эллипсоида. Отношение частного масштаба к главному, обозначаемое через μ, характеризует искажение длин 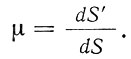 (2.2) (2.2)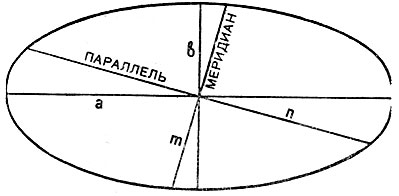 Рис. 2.1. Эллипс искажений и его элементы В любой точке на поверхности эллипсоида имеются два взаимно перпендикулярных направления (называемых главными), которые в проекции также изображаются взаимно перпендикулярными линиями, совпадающими с большой и малой осями эллипса искажения (рис. 2.1). Очевидно, в эллипсе искажений наибольший масштаб совпадает с направлением большой оси эллипса, а наименьший с направлением малой оси. Экстремальные масштабы по главным направлениям, выраженные в отношении к главному масштабу, обозначают соответственно через а и b. Вообще, главные направления могут не совпадать с меридианами и параллелями (и их изображением в проекции). В таком случае масштабы по меридиану и параллели обозначают соответственно через т и п. Непостоянство масштабов в данной точке по разным направлениям можно видеть на рис. 2.2, б, где длины изображаемых меридианов равны длинам меридианов эллипсоида (разумеется, с уменьшением до масштаба карты), а длины параллелей увеличиваются по мере удаления от экватора. На рисунке отрезки параллелей между двумя меридианами одинаковы на любой широте, тогда как в действительности они уменьшаются с приближением к полюсу до нуля. Таким образом, масштаб вдоль меридианов постоянен в любой точке карты, но вдоль параллелей он возрастает с увеличением широты. Это видно по эллипсам искажений, показанным на рис. 2.2, б. Наряду с искажениями длин различают искажения площадей и углов. За искажение площади в некоторой точке карты принимают отношение площади эллипса искажений dP, к площади dP соответствующего бесконечно малого круга на эллипсоиде, обозначаемое через р: 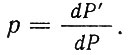 (2.3) Искажением угла называют разность между углом, образованным двумя линиями на эллипсоиде, и изображением этого угла на карте. Величина искажения углов в данной точке характеризуется наибольшим значением этой разности ω. 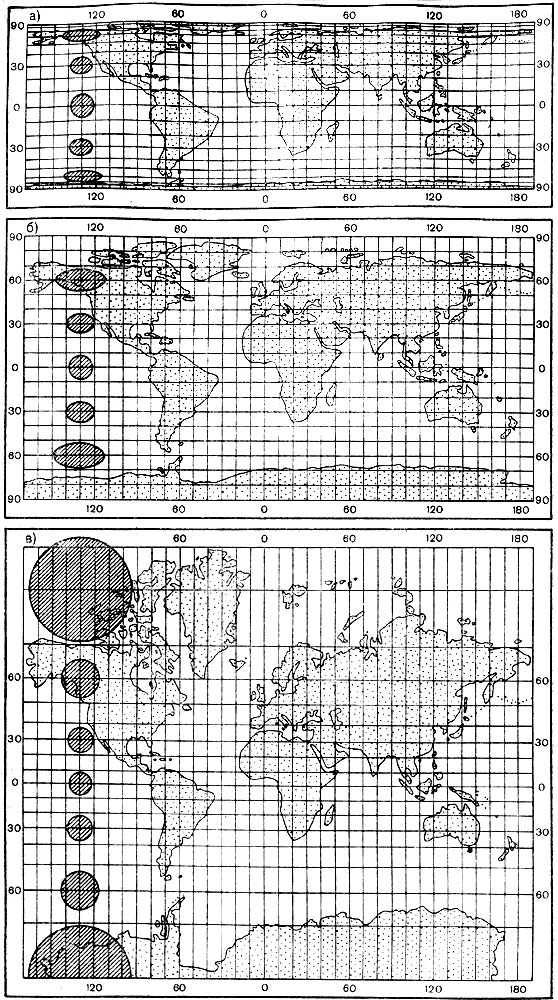 Рис. 2.2. Картографические сетки в цилиндрических проекциях: а - равновеликой; б - равнопромежуточной; в - равноугольной (Меркатора) Проекций, совершенно лишенных искажений длин, не существует. Такие проекции сохраняли бы подобие и пропорциональность всех частей земной поверхности, что может иметь место только на модели эллипсоида. Вместе с тем есть проекции, свободные от искажения углов или от искажений площадей. Проекции, которые передают величину углов без искажения и сохраняют подобие бесконечно малых фигур, называются равноугольными. Одна из них изображена на рис. 2.2, в. В каждой точке равноугольной проекции масштаб одинаков на всех направлениях (эллипс искажений превращается в окружность), но меняется от точки к точке. Это видно по изменению размеров окружностей - эллипсов искажений. Равновеликие проекции сохраняют площади (эллипсы искажений везде имеют одинаковую площадь), но сильно нарушают подобие фигур (вытянутость эллипсов искажений различна) (см. рис. 2.2, а). Существует множество проекций, которые не являются ни равноугольными, ни равновеликими, - их называют произвольными. Но нет и не может быть проекции, которая была бы одновременно равноугольной и равновеликой. Вообще, чем больше искажения углов, тем меньше искажения площадей и наоборот. Среди произвольных проекций выделяют равнопромежуточные, во всех точках которых масштаб по одному из главных направлений постоянен и равен главному масштабу (например, по меридианам или параллелям в проекциях, где они совпадают с главными направлениями). По своим свойствам произвольные проекции лежат между равноугольными и равновеликими. Характер искажений, присущий проекции (равноугольная, равновеликая, равнопромежуточная), отмечается в ее названии. § 2.2 Классификация проекций по виду меридианов и параллелей нормальной сетки В картографической практике распространена классификация проекций по виду вспомогательной геометрической поверхности, которая может быть использована при их построении. С этой точки зрения выделяют проекции: цилиндрические, когда вспомогательной поверхностью служит боковая поверхность цилиндра, касательного к эллипсоиду, или секущего эллипсоид; конические, когда вспомогательной плоскостью является боковая поверхность касательного или секущего конуса; азимутальные, когда вспомогательная поверхность - касательная или секущая плоскость. Геометрическое построение названных проекций отличается большой наглядностью. Для простоты рассуждения вместо эллипсоида воспользуемся шаром. Заключим шар в цилиндр, касательный по экватору (рис. 2.3, а). Продолжим плоскости меридианов ПА, ПБ, ПВ, ... и примем пересечения этих плоскостей с боковой поверхностью цилиндра за изображение на ней меридианов. Если разрезать боковую поверхность цилиндра по образующей аАа1 и развернуть ее на плоскость, то меридианы изобразятся параллельными равноотстоящими прямыми линиями аАа1, бБб1, вВв1 ..., перпендикулярными экватору АБВ. Изображение параллелей может быть получено различными способами. Один из них - продолжение плоскостей параллелей до пересечения с поверхностью цилиндра, что даст а развертке второе семейство параллельных прямых линий, перпендикулярных меридианам. 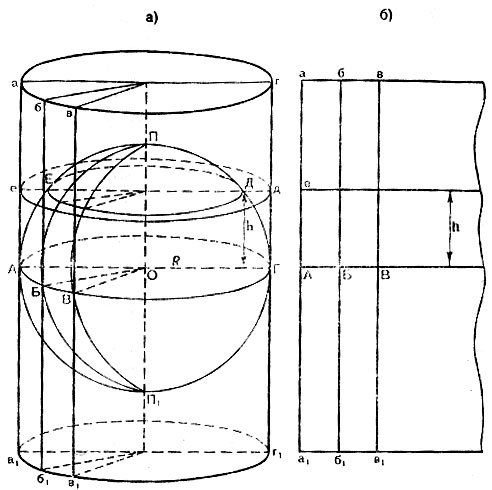 Рис. 2.3. Построение картографической сетки в равновеликой цилиндрической проекции Полученная цилиндрическая проекция (рис. 2.3, б) окащывается равновеликой, так как боковая поверхность шарового пояса АЕДГ, равная 2πRh (где h - расстояние между плоскостями АГ и ЕД), соответствует площади изображения этого пояса в развертке. Главный масштаб сохраняется вдоль экватора; частные масштабы по параллели увеличиваются, а по меридианам уменьшаются по мере удаления от экватора. Другой способ определения положения параллелей основан на сохранении длин меридианов, т. е. на сохранении главного масштаба вдоль всех меридианов. В этом случае цилиндрическая проекция равно-промежуточна по меридианам (см. рис. 2.2,6). Для равноугольной цилиндрической проекции необходимо в любой точке постоянство масштаба по всем направлениям, что требует увеличения масштаба вдоль меридианов по мере удаления от экватора в соответствии с увеличением масштабов вдоль параллелей на соответствующих широтах (см. рис. 2.2, в). Нередко вместо касательного цилиндра используют цилиндр, секущий шар по двум параллелям (рис. 2.4), вдоль которых при развертке сохраняется главный масштаб. В этом случае частные масштабы вдоль всех параллелей между параллелями сечения будут меньше, а на остальных параллелях - больше главного масштаба. 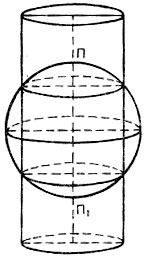 Рис. 2.4. Цилиндр, секущий шар по двум параллелям Для построения конической проекции заключим шар в конус, касающийся шара по параллели АБВГ (рис. 2.5, а). 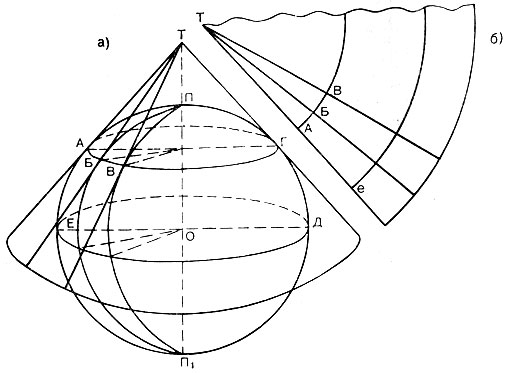 Рис. 2.5. Построение картографической сетки в равнопро-межуточной конической проекции Аналогично предыдущему построению продолжим плоскости меридианов ПА, ПБ, ПВ, ... и примем их пересечения с боковой поверхностью конуса за изображение на ней меридианов. После развертки боковой поверхности конуса на плоскости (рис. 2.5, б) меридианы изобразятся радиальными прямыми ТА, ТБ, ТВ,..., исходящими из точки Г, причем углы между ними будут пропорциональны (но не равны) разностям долгот. Вдоль параллели касания АБВ (дуги окружности радиусом ТА) сохраняется главный масштаб. 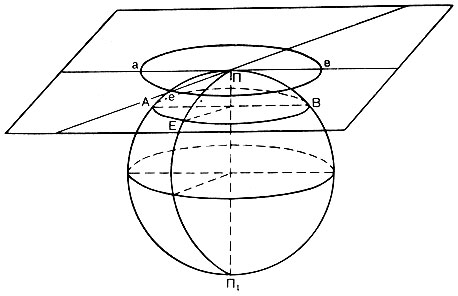 Рис. 2.6. Построение картографической сетки в азимутальной проекции  Рис. 2.7. Эмблема ООН - равнопромежуточная азимутальная проекция Положение других параллелей, изображающихся дугами концентрических окружностей, можно определить из разных условий, одно из которых - сохранение главного масштаба вдоль меридианов (АЕ=Ае) - приводит к конической равнопромежуточной проекции. Для построения азимутальной проекции воспользуемся плоскостью, касательной к шару в точке полюса П (рис. 2.6). 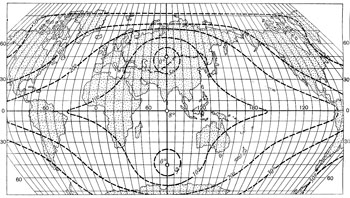 Рис. 2.8 Картографическая сетка в одной из псевдоцилиндрических проекций (с изоколами углов) 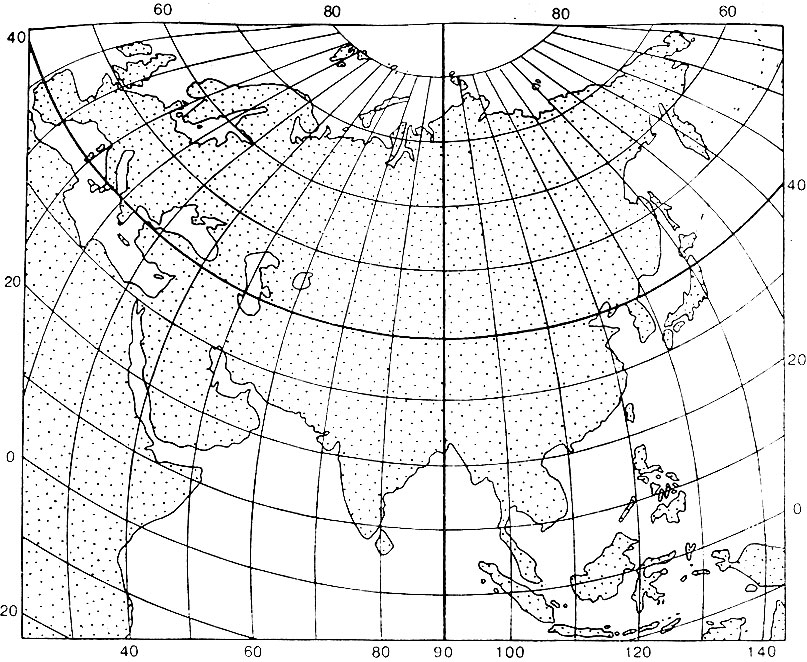 Рис. 2.9. Картографическая сетка в одной из псевдоконических проекций 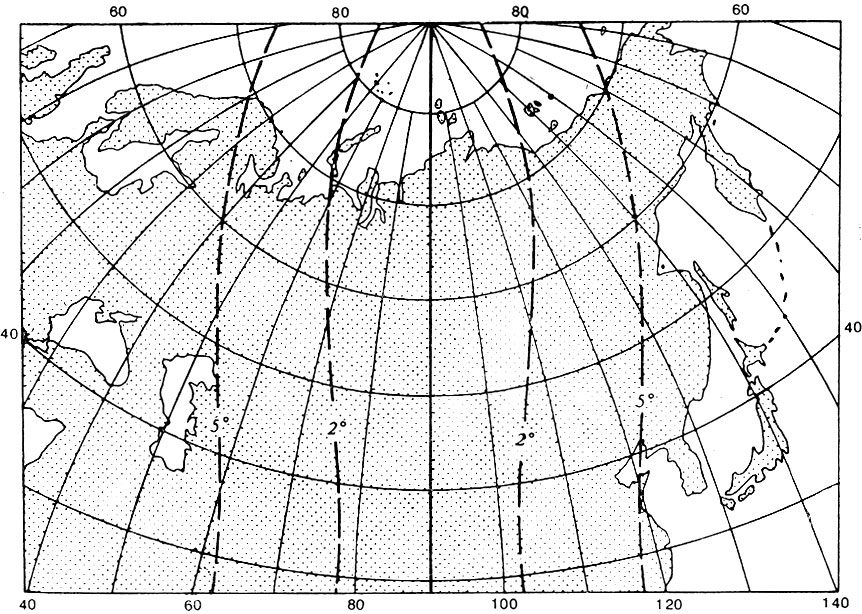 Рис. 2.10. Картографическая сетка в одной из поликонических проекций (с изоколами углов) Пересечения плоскостей меридианов с касательной плоскостью дают изображение меридианов Па, Пе, Пв,... в виде прямых, углы между которыми равны разностям долгот. Параллели, являющиеся концентрическими окружностями, могут быть определены различным путем, например, проведены радиусами, равными выпрямленым дугам меридианов от полюса до соответствующей параллели ПА=Па. Такая проекция равнопромежуточна по меридианам и сохраняет вдоль них главный масштаб. Например, эта проекция использована на эмблеме ООН (рис. 2.7). Проекция, при построении которых оси цилиндра и конуса совмещались с полярной осью земного шара, а плоскость размещалась касательно в точке полюса, называются нормальными. К нормальным по виду сетки относят также проекции: псевдоцилиндрические, у которых параллели - прямые, параллельные друг другу, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана (рис. 2.8); псевдоконические, где параллели - дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана (рис. 2.9); поликонические,параллели которых - дуги эксцентрических окружностей с центрами на среднем прямолинейном меридиане а меридианы - кривые' симметричные относительно среднего меридиана (рис. 2-Ю), а также некоторые Другие, рассматриваемые в курсе математической картографии. 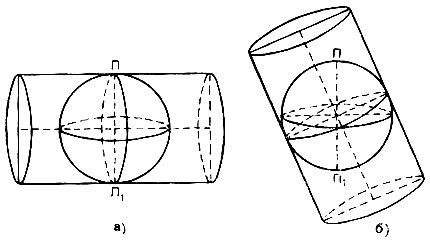 Рис. 2.11. Положение цилиндра при поперечной (а) и косой (б) цилиндрических проекциях Для цилиндрических и азимутальных проекций наряду с нормальной широко используют другие ориентировки цилиндра и плоскости: поперечные, когда ось цилиндра лежит в плоскости экватора (рис. 2.11 а), а плоскость касается шара в одной из точек экватора; косые, когда ось цилиндра (рис. 2.11, б) образует с полярной осью острый угол, а плоскость касается шара в какой-либо точке между полюсом и экватором. Вообще говоря, сетки меридианов и параллелей в поперечных и косых цилиндрических и азимутальных проекциях образуются кривыми линиями, и потому классификация проекций по виду меридианов и параллелей производится применительно к нормальным сеткам. Среди азимутальных проекций выделяют перспективные, получаемые проектированием поверхности шара на плоскость по закону перспективы посредством лучей из точки зрения, располагаемой на прямой, проходящей через центр шара и перпендикулярной плоскости касания (картинной плоскости). В частности, различают перспективные проекции: ортографические, когда точка зрения удалена в бесконечность и проектирование производится пучком параллельных лучей (рис. 2.12); в этой проекции мы практически видим поверхность Луны; в ней изображен земной шар на гербе СССР; стереографические, когда точка зрения располагается на поверхности шара и диаметрально противоположна точке касания картинной плоскости, стереографическая проекция равноугольна; любая окружность на поверхности шара изображается в этой проекции также окружностью; гномонические, когда точка зрения находится в центре шара; в этой проекции дуги всех больших кругов шара изображаются прямыми линиями. Проекции, которые по виду сетки не подходят под рассмотренные, называются условными. 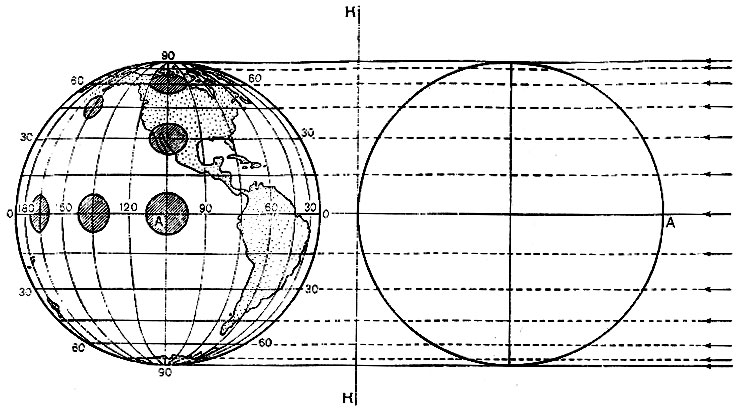 Рис. 2.12. Построение картографической сетки в поперечной ортографической проекции: в правой части рисунка - проектирование пучком параллельных лучей на картинную плоскость КК, перпендикулярную плоскости рисунка; в левой - разворот картинной плоскости В практике современной картографии сетки получаются не посредством геометрических построений, а расчетным, аналитическим путем. В результате вычислений по формулам проекции определяют прямоугольные координаты пересечений меридианов и параллелей (узловых точек сетки), величину и распределение искажений; наносят узловые точки сетки и по ним проводят меридианы и параллели. В настоящее время для изыскания и вычисления картографических проекций широко используются электронно-вычислительные машины и автоматическое построение сеток на графопостроителях - чертежных машинах автоматического действия. Имеется сводка с подробными справочными данными о проекциях и других элементах математической основы советских карт (См.: Гинзбург Г. А., Карпов Н. С, Салманова Т. Д. Математическая картография в СССР, ч. 1. Исторический очерк и справочные данные//Тр. ЦНИИГАиК, 1955, вып. 99. С. 88-183.). В ней для каждой проекции указаны характер искажений, ее параметры и во многих случаях помещены чертежи проекции с изоколами искажений площадей р и углов сэ (см. § 2.3). Для выбора картографических проекций опубликован специальный атлас (См.: Гинзбург Г. А., Салманова Т. Д. Атлас для выбора картографических проекций//Тр. ЦНИИГАиК, 1957, вып. 110. 237 с.). § 2.3 Искажения в картографических проекциях; их распределение; определение размеров искажений на картах Искажение (деформация) изображения, выражающееся в изменениях масштаба длин, присуще всем картографическим проекциям, - это их основное свойство. Но проекции различаются по характеру искажений (равноугольные, равновеликие, равнопромежуточные произвольные), по величине искажений и их распределению. Вообще говоря, проекции могут иметь отдельные точки, линии или даже систему линии, где сохраняется главный масштаб. В азимутальных проекциях - это точка касания плоскости, в конических - параллель касания конуса (или параллели сечения) и т. п. Такие точки и линии называются точками и линиями нулевых искажений. Искажения возрастают по мере удаления от точек или линий нулевых искажении. Другими словами, они возрастают с увеличением размеров картографируемой территории.  Рис. 2.13. Изоколы площадей в равноугольной цилиндрической проекции Меркатора Для оценки достоинств проекции используют показатели искажения площадей р и углов ω, определяемые при вычислении проекции. Определение этих величин для ряда точек картографической сетки и последующее проведение по ним изокол - линий, соединяющих точки с одинаковыми значениями искажений площадей и углов, дает наглядную картину распределения искажений и позволяет учитывать искажения при пользовании картой. В нормальных цилиндрических проекциях (рис. 2.13) изоколы располагаются параллельно экватору (или параллелям сечения); в нормальных конических проекциях - параллельно параллели касания (или параллелям сечения); в нормальных азимутальных проекциях изоколы параллельны концентрическим окружностям параллелей. Очевидно, нормальные цилиндрические проекции целесообразно применять для изображения экваториальной зоны и вообще территорий, вытянутых вдоль экватора; нормальные конические проекции - для территорий, лежащих в средних широтах и вытянутых с востока на запад (например, для СССР); нормальные азимутальные проекции - для полярных районов.  Рис. 2.14. Картографическая сетка в экваториальной стереографической проекции с изоколами площадей Также легко представить расположение изокол в поперечных и косых проекциях. Например, в поперечной цилиндрической проекции изоколы параллельны меридиану касания, и, следовательно, такие проекции выгодны для передачи территорий, вытянутых вдоль этого меридиана с севера на юг. В любой азимутальной проекции изоколы образуют окружности, концентрические относительно точки касания плоскости (рис. 2.14 и 2.15); поэтому азимутальные проекции удобны для территорий округлой формы (при центральном положении точки касания). В произвольных проекциях изоколы могут образовывать сложную систему кривых линий (см. рис. 2.8). В математической картографии доказывается, что при изображении конкретных территорий наименьшие искажения обеспечиваются проекциями, у которых изоколы по своей форме близки к общему контуру картографируемой территории. Важно знать, что при наличии картографической сетки величина искажений может быть определена на любом участке карты, еслв даже проекция не указана.  Рис. 2.15. Картографическая сетка в экваториальной равновеликой азимутальной проекции (Ламберта) с изоколами углов Для этого достаточно определить в соотвествующем месте карты масштабы по меридиану и параллели т и п, а также угол θ между меридианом и параллелью. Для нахождения величин т и п следует: а) измерить дуги меридиана и параллели возле соответствующей узловой точки картографической сетки; б) определить масштаб по меридиану и параллели посредством деления полученных величин на длины соответствующих дуг эллипсоида (заимствуемые из картографических таблиц). Найти величины т и п посредством деления масштабов по меридиану и параллели на главный масштаб. Угол θ между меридианом и параллелью измеряется транспортиром. Для вычисления по величинам т, п и углу θ значений а, b, р, и угла θ математическая картография дает следующие несложные формулы: (2.4) 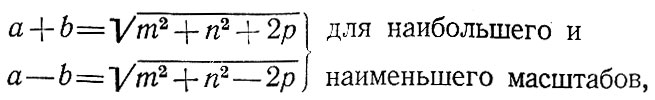 (2.5), (2.6) 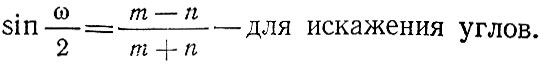 (2.7) Если главные направления совпадают с меридианами и параллелями, т. е. когда меридианы и параллели сетки взаимно перпендикулярны, то а=т, b=п (или а=п, b=т) и формулы приобретают вид 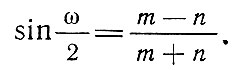 (2.9) (2.9) |
