ИМ-3 Арм 5. Казахская головная архитектурностроительная академия
 Скачать 60.89 Kb. Скачать 60.89 Kb.
|
|
Активный раздаточный материл КАЗАХСКАЯ ГОЛОВНАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ
Краткое содержание лекции Определение перемещений в системах При воздействии нагрузки, температуры и других факторов сооружения меняют свою форму, а его точки получают перемещения. Перемещение – векторная величина. Перемещение любой точки на плоскости можно задать через его модуль и направление. Поступательные перемещения 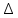 A, A, 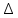 xA, xA, 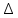 yA будем называть линейными перемещениями, а yA будем называть линейными перемещениями, а 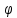 A – угловым перемещением. A – угловым перемещением.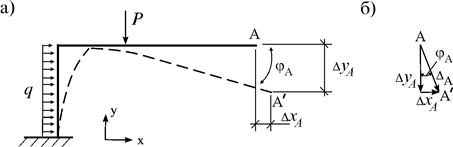 Рис.1 Действительным перемещением называется перемещение, вызванное силой по направлению ее действия (рис.2а). В упругих системах перемещение 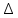 прямо пропорционально действующей силе и поэтому выполняется закон Гука прямо пропорционально действующей силе и поэтому выполняется закон Гука 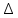 =d P, где коэффициент dназывается податливостью. =d P, где коэффициент dназывается податливостью.Эту зависимость можно представить в виде диаграммы 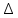 –P (рис.2б). –P (рис.2б).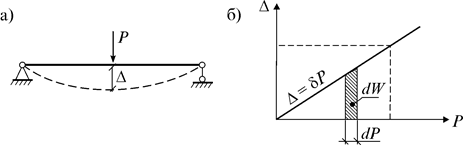 Рис.2 Действительной работой называется работа силы на ее действительном перемещений. Действительную работу силы P можно найти по рис.2б: А= Эта формула определяет теорему Клапейрона: сила, действующая на упругую систему, совершает работу, равную половине произведения силы на перемещение. Когда на систему действуют несколько сил, то по принципу суперпозиции А= В идеально-упругой системе предполагается, что работа внешних сил А полностью переходит в потенциальную энергию деформацииU: А =U. Если убрать внешние силы, упругая система возвратится в исходное положение. Эту работу совершают внутренние силы. Так как работа внешних сил А всегда положительна, то работа внутренних сил V будет отрицательной: А=–V. Определим работу внутренних сил плоской стержневой системы. 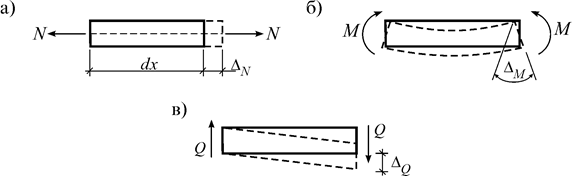 Рис.3 Пара продольных сил N, действующих на элементdx, приводят к его чистому растяжению (рис.3а). −dVN= Пара изгибающих моментовM, действующих на элемент dx, приводят к его чистому изгибу (рис.3б). –dVM= 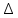 M. M.Действие пары поперечных сил Q приводит к чистому сдвигу элемента dx(рис.3в). –dVQ= 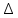 Q. Q. Теперь воспользуемся принципом суперпозиции: –dV=–(dVM+dVQ+dVN)= Если проинтегрировать это выражение по всей длине элемента l и учесть наличие в системе n стержней, получим выражение потенциальной энергии всей стержневой системы: U= –V= Контрольные вопросы: Теория перемещений. Общие понятия. Теорема о взаимности работ? Теорема о взаимности реакций? Теорема о взаимности перемещений? Глоссарий
Задание на СРС: Потенциальная энергия деформации при растяжении и сжатии. Реферат. Задание на СРСП: Правило Верещагина. Умножение эпюр. Литература: Основная: І. Анохин Н.Н. Строительная механика в примерах и задачах. -М., АСВ, ч.1,2. 2010. 2. Ржаницын А.Р. Строительная механика. –М., ВШ, 1991. 3. Леонтьев Н.Н. и др. Строительная механика. М., АСВ, 2006. 4. Кроткова Л.В., Филлипович А.И. и др. Сборник задач по строительной механике. –М., АСВ, 2011. 5. Руководство к практическим занятиям по курсу строительной механики. Под ред. Г.К. Клейна. М: Высшая школа, 1980. Дополнительная: І. Леонтьев Н.Н. Основы строительной механики стержневых систем. Учебник для вузов. М.: Высшая школа, 1996. 2. Смирнов А.Ф. и др. Строительная механика. Стержневые системы, Учебник для вузов. М.: Стройиздат, 1981. 3. Тулебаев К.Р., Полякова И.М. Расчет стержневых систем. 1999г. 5. Достанова С.Х., Касымова Г.Т. Құрылыс механикасының есептерін шығаруға арналған жетекшілік. Алматы, ХББК, 2011. -112б. |
