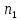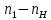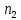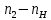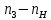Расчет зубчатого механизма. Вариант 2Б. Кинематический анализ сложного эпициклического зубчатого механизма
 Скачать 263.03 Kb. Скачать 263.03 Kb.
|
|
Министерство образования и науки Российской Федерации Омский государственный технический университет Кафедра «Теория механизмов и машин» ДОМАШНЕЕ ЗАДАНИЕ Тема: «Кинематический анализ сложного эпициклического зубчатого механизма» Дисциплина: Прикладная механика» Вариант 2/Б Автор___________ ________ __________ подпись дата Фамилия И.О. Группа:_________ Руководитель___________ ________ __________ подпись дата Фамилия И.О. Омск 2013 СОДЕРЖАНИЕ Введение Техническое задание Раздел 1. Кинематический анализ механизма Аналитический расчет Графический расчет дифференциального зубчатого механизма Построение картины линейных скоростей Построение плана чисел оборотов Определение погрешности Раздел 2. Назначение числа сателитов по условию соседства Заключение Список литературы Введение Механизм – это искусственно созданная система, предназначенная для преобразования движений одних звеньев в требуемые движения других. В расчетно-графической работе было выполнено кинематическое исследование дифференциального зубчатого механизма с замкнутым контуром. Расчет выполнен двумя методами: графическим и аналитическим. Объем записки составляет 12 листов. Записка содержит 2 рисунка. Библиографический список включает три наименования.  Раздел 1. Кинематический расчет механизма 1.1 Аналитический расчет Исследуемый дифференциальный механизм представляет собой соединения двух простых механизмов: ступенчатого и планетарного. Первоначально определим неизвестные числа зубьев колес 3 и 5 по условию соосности [2] . Из условия соосности колес 1,2,3: 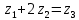 , ,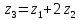 , ,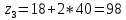 . .Из условия соосности колес 4,5,6: 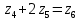 , ,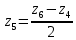 , ,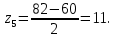 Для каждого механизма составим формулу передаточного отношения. Так как для механизма I имеем: 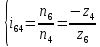 (1.1) (1.1)Учитывая, что 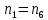 , уравнение 1.1 примет вид: , уравнение 1.1 примет вид: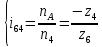 (1.2) (1.2)Для механизма II применяем метод Виллиса, останавливаем водило Н , соответственно придаем механизму обороты равные - 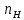 (табл. 1) (табл. 1)Таблица 1
Следовательно таблице 1, передаточное отношение для механизма II определится как: 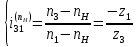 (1.3) (1.3)Учитывая что 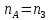 , (1.3) примет вид: , (1.3) примет вид: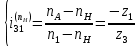 (1.4) (1.4)Уравнения (1.2) и (1.4) решаем совместно: 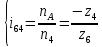 , ,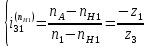 . .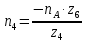 , ,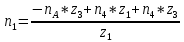 . .Принимая во внимание, что 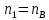 , ,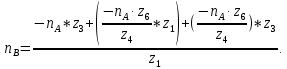 Подставляя численные значения чисел зубьев и числа оборотов, определяем число оборотов вала В: 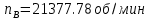 1.2 Графический расчет механизма Определеним радиусы делительных окружностей колес по формуле [1,2]: 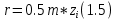 , ,где 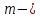 модуль зубчатых колес модуль зубчатых колес 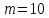 ; ;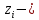 число зубьев; число зубьев;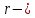 радиус делительной окружности. радиус делительной окружности.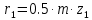 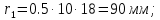 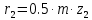 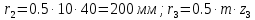 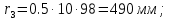 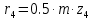 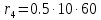 = 300мм; = 300мм;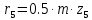 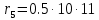 =55мм; =55мм;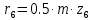 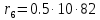 =410мм. =410мм.Вычерчиваем схему механизма в масштабе 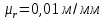 Обозначаем О1, О2, О3, О4,О5 – оси колес и саттелитов; a,b,c,d– точки контакта делительных окружностей – высшие кинематические пары. 1.2.1 Построение картины линейных скоростей Рассматриваем систему координат [r,V]. На ось r проецируем обозначенные точки контакта. Определяем угловые скорости[1,2]: 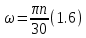 Угловая скорость вала А: 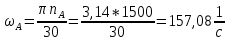 Известные линейные скорости определим по формуле[1,2]: 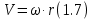 Линейная скорость точки a: 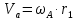 , ,где 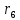 - радиус делительной окружности колеса 6. - радиус делительной окружности колеса 6.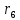 = 0,41 м. = 0,41 м.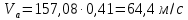 . .При построении картины скоростей учитываем, что известна скорость точки a. на картине скоростей изобразим ее отрезком aa` в масштабе 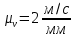 (aa` = (aa` =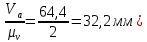 .Ось О5 неподвижна, что позволяет построить картину скоростей для шестого и третьего колеса и определить скорость точки b (отрезок bb`). По картине распределения скоростей для колеса 4 и определяем скорость оси О2 (отрезок О2О2`). По известной скорости точки с строим картину распределения колеса 2 и определяем скорость точки d (отрезок dd`) (рис.1.1). .Ось О5 неподвижна, что позволяет построить картину скоростей для шестого и третьего колеса и определить скорость точки b (отрезок bb`). По картине распределения скоростей для колеса 4 и определяем скорость оси О2 (отрезок О2О2`). По известной скорости точки с строим картину распределения колеса 2 и определяем скорость точки d (отрезок dd`) (рис.1.1). 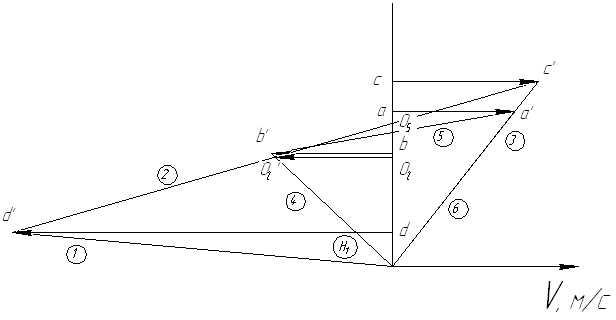 Рис. 1.1 Картина скоростей 1.2.2 План чисел оборотов Ниже картины скоростей проводим горизонтальную прямую. Это ось чисел оборотов. Выбираем длину отрезка Оn6, которым удобно изобразить число оборотов колеса 1 (Оn6=7,5мм). Масштабный коэффициент плана чисел оборотов: 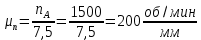 Из точки n6проводим луч, параллельный отрезку О1а`, он пересекает вертикальную прямую в точке р. Из точки р проводим луч, параллельный отрезку О1d`(рис 1.3).  Рис. 1.3 План чисел оборотов Для определения числа оборотов вала В измерим отрезок Оn1 и умножим его на масштабный коэффициент (Оn1=106,88мм): 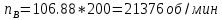 Определение погрешности Для определения правильности выполнения расчета, определим погрешность: 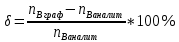 где 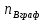 – число оборотов, найденное графическим методом – число оборотов, найденное графическим методом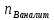 – число оборотов, найденное аналитическим методом – число оборотов, найденное аналитическим методом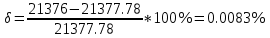 Погрешность меньше 5 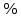 , что свидетельствует о правильности выполнения расчета[1]. , что свидетельствует о правильности выполнения расчета[1].Раздел 2. Назначение числа сателлитов по условию соседства. В данной работе необходимо назначить число сателлитов 2 по условию соседства. Условие соседства: 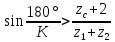 , ,где К – число сателлитов; zc – число зубьев сателлита; В нашем случае: zc = z2, тогда 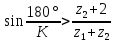 , ,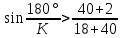 , ,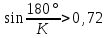 , отсюда следует, что минимальное число сателлитов может быть 2. , отсюда следует, что минимальное число сателлитов может быть 2. Заключение Выполнен кинематический расчет зубчатого механизма. Расчет выполнен аналитическим и графическим методами. Построены картины скоростей и чисел оборотов. Погрешность проведенного расчета составляет 0.0083%, что свидетельствует о правильности выполнения расчета. Список литературы 1. Н.Н. Федоров. Проектирование и кинематика плоских механизмов. Учебное пособие. Омск, изд-во ОмГТУ, 2000. 2. Артоболевский И. И. Теория механизмов и машин. Учебник для вузов - М.: Наука, 1988. |