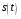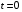Решение варианта 551. Кинематическое исследование движения точки
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Расчётно-графическая работа № 1 на тему: «Кинематическое исследование движения точки» Исходные данные: 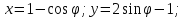 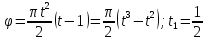 c. c.Решение:
Для определения траектории точки выразим 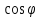 и и 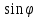 , после чего возведем выражения в квадрат и затем их сложим: , после чего возведем выражения в квадрат и затем их сложим: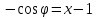 , , 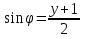 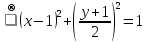 Таким образом, получили, что траектория точки – это эллипс с центром в точке 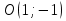 и полуосями и полуосями 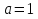 м, м, 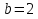 м. м.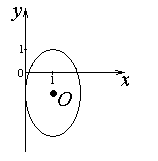
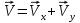 ; ;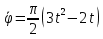 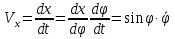 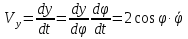 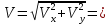 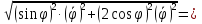 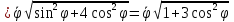 . .
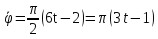 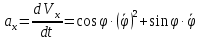 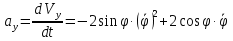 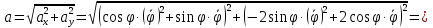 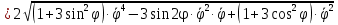
Найдем начальное положение точки в момент времени  c: c: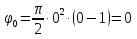 рад; рад;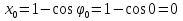 м; м;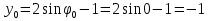 м; м;Проекции и модуль вектора скорости в начальный момент времени 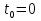 c: c: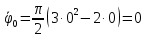 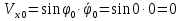 м/с; м/с;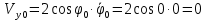 м/с; м/с;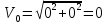 м/с. м/с.Проекции и модуль вектора ускорения в начальный момент времени 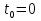 c: c: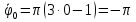 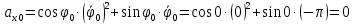 м/с2 м/с2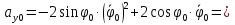 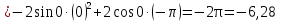 м/с2; м/с2;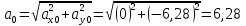 м/с2. м/с2.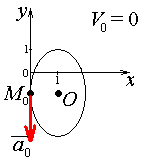
В качестве начала отсчёта дуговой координаты возьмем точку  , направление отсчёта – против хода часовой стрелки. , направление отсчёта – против хода часовой стрелки.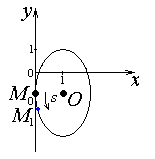 Изменение дуговой координаты по времени можно найти следующим образом: 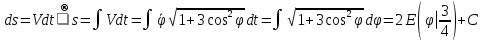 . .Так как начало отчета мы совместили с точкой 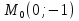 , то при , то при 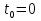 c: c: 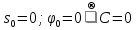 . . Таким образом, 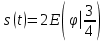 или или 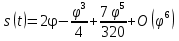 , где , где 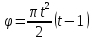 . .
Касательное ускорение точки: 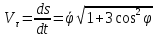 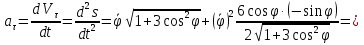 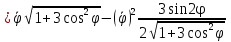 Нормальное ускорение точки: 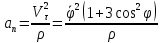 где 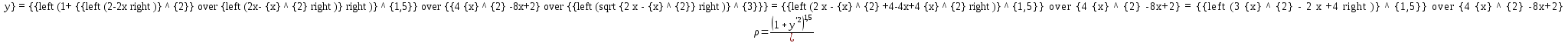 - радиус кривизны траектории движения точки выводится из уравнения эллипса - радиус кривизны траектории движения точки выводится из уравнения эллипса 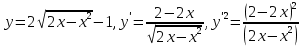 , ,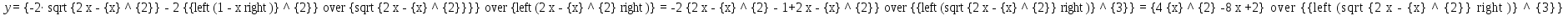 . .
График зависимости от времени дуговой координаты 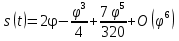 : :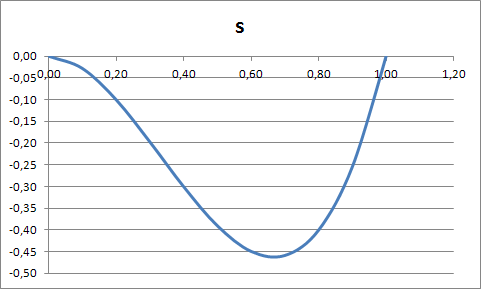 График зависимости от времени проекции вектора скорости на касательную 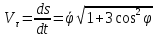 : :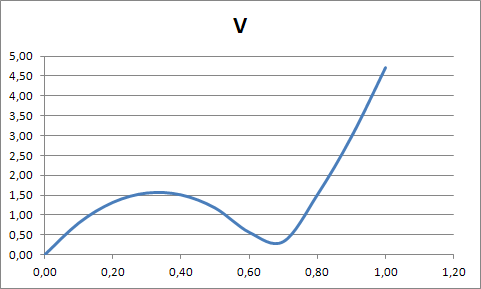 График зависимости от времени касательного ускорения 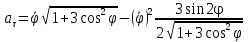 : :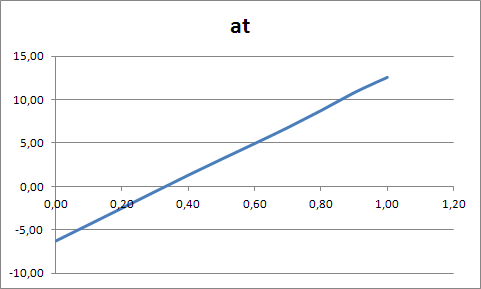 График зависимости от времени пройденного пути 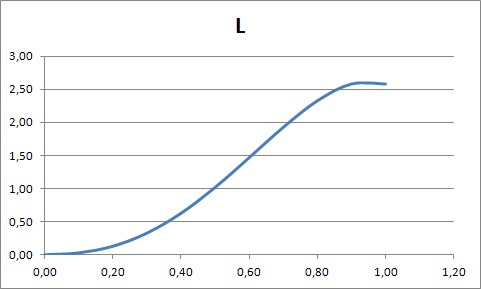
Найдем положение точки в заданный момент времени 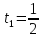 c: c: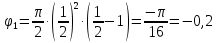 рад; рад;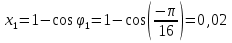 м; м;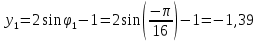 м; м;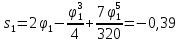 м. м.Проекции и модуль вектора скорости в заданный момент времени 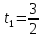 c: c: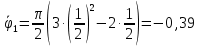 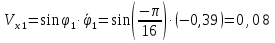 м/с; м/с;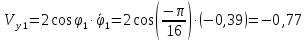 м/с; м/с;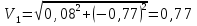 м/с. м/с.Найдем направляющий косинус вектора скорости 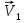 (угол, который образует вектор скорости (угол, который образует вектор скорости 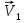 с положительным направлением оси х) с положительным направлением оси х)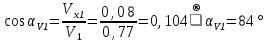 Проекции и модуль вектора ускорения в заданный момент времени 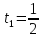 c: c: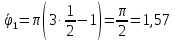 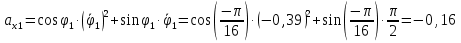 м/с2 м/с2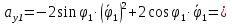 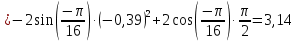 м/с2; м/с2;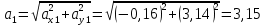 м/с2. м/с2.Найдем направляющий косинус вектора ускорения 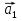 (угол, который образует вектор ускорения (угол, который образует вектор ускорения 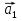 с положительным направлением оси х): с положительным направлением оси х):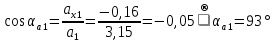 . .Касательное и нормальное ускорения в заданный момент времени  c: c: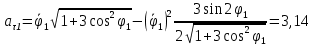 м/с2; м/с2;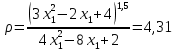 м м 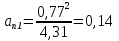 м/с2. м/с2.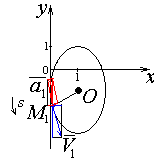 Расчётно-графическая работа № 3 на тему: «Сложное движение точки» По ободу диска радиуса  движется точка движется точка 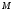 . Уравнение движения задано в таблице; там же указано начало отсчёта . Уравнение движения задано в таблице; там же указано начало отсчёта 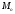 дуговой координаты дуговой координаты  . Положительное направление отсчёта – по ходу часовой стрелки, если смотреть навстречу оси . Положительное направление отсчёта – по ходу часовой стрелки, если смотреть навстречу оси  . Уравнение вращения диска задано в таблице. Положительным направлением вращения считается направление против хода часовой стрелки, если смотреть с положительного конца . Уравнение вращения диска задано в таблице. Положительным направлением вращения считается направление против хода часовой стрелки, если смотреть с положительного конца  оси вращения оси вращения  . Для момента времени . Для момента времени 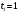 с определить абсолютную скорость и абсолютное ускорение точки с определить абсолютную скорость и абсолютное ускорение точки 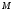 . .Исходные данные: 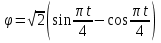 , , 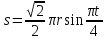 , , 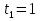 c. c.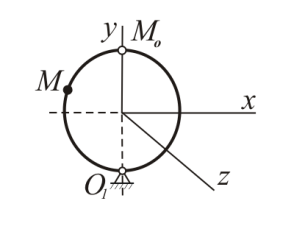 Найти: абсолютную скорость 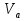 и абсолютное ускорение и абсолютное ускорение 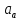 точки М для момента времени точки М для момента времени 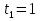 c. c.Решение: Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью диска. Положение точки М на диске определяется расстоянием 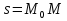 . . При 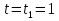 с: с: 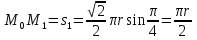 . Найдем угол, на который повернулся радиус при движении точки М по окружности: . Найдем угол, на который повернулся радиус при движении точки М по окружности: 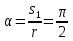 рад. рад.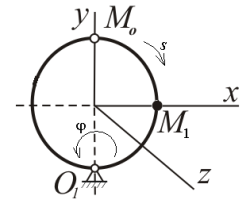 Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей: 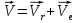 . . Модуль относительной скорости 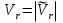 , где , где 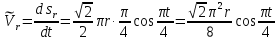 При 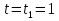 с: с: 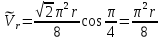 ; ; 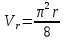 . . Положительный знак у 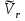 показывает, что вектор показывает, что вектор 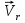 направлен в сторону положительных значений направлен в сторону положительных значений 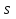 , перпендикулярно радиусу окружности, то есть вертикально вниз. , перпендикулярно радиусу окружности, то есть вертикально вниз. Модуль переносной скорости 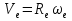 , где , где 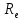 – радиус окружности, описываемой той точкой тела, с которой в данный момент совпадает точка М, – радиус окружности, описываемой той точкой тела, с которой в данный момент совпадает точка М, 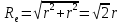 ; ; 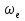 - модуль угловой скорости тела: - модуль угловой скорости тела: 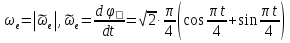 . .При 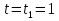 с: с: 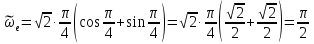 ; ; 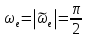 . .Положительный знак у величины 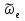 показывает, что вращение диска происходит вокруг оси показывает, что вращение диска происходит вокруг оси 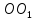 в сторону отсчета угла в сторону отсчета угла 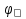 . Поэтому вектор . Поэтому вектор 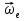 направлен по оси направлен по оси 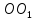 , перпендикулярно плоскости рисунка на нас (параллельно оси z). , перпендикулярно плоскости рисунка на нас (параллельно оси z).Таким образом, модуль переносной скорости при 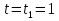 с равен с равен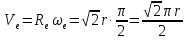 . .Вектор 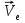 направлен перпендикулярно радиусу направлен перпендикулярно радиусу 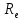 в сторону вращения. в сторону вращения.Модуль абсолютной скорости точки М находим способом проекций: 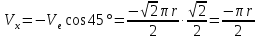 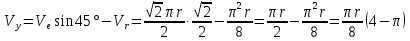 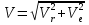 или или 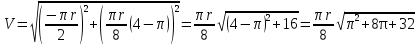 . .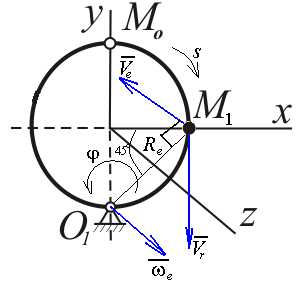 Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений: 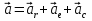 , или в развернутом виде , или в развернутом виде 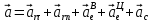 . .Модуль относительного касательного ускорения 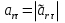 , где , где 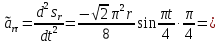 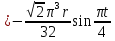 . .При 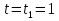 с: с: 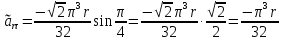 ; ; 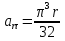 . .Отрицательный знак  показывает, что вектор показывает, что вектор  направлен в сторону отрицательных значений направлен в сторону отрицательных значений  , перпендикулярно радиусу окружности, то есть вертикально вверх. Знаки , перпендикулярно радиусу окружности, то есть вертикально вверх. Знаки 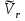 и и 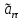 не одинаковы; следовательно, относительное движение точки М замедленное. не одинаковы; следовательно, относительное движение точки М замедленное.Относительное нормальное ускорение 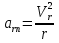 , то есть при , то есть при 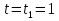 с: с: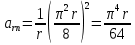 . .Вектор 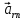 направлен к центру диска, то есть горизонтально влево. направлен к центру диска, то есть горизонтально влево.Модуль переносного вращательного ускорения 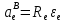 , где , где 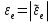 – модуль углового ускорения диска: – модуль углового ускорения диска: 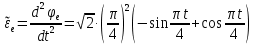 . .При  с: с: 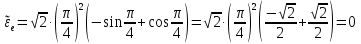 ; ; 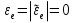 . .Таким образом, получаем 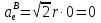 . . Модуль переносного центростремительного ускорения 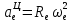 или или 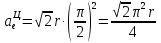 . .Вектор 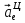 направлен к центру вращения направлен к центру вращения 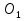 . .Кориолисово ускорение 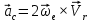 . Модуль кориолисова ускорения . Модуль кориолисова ускорения 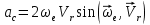 , где , где 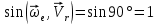 . .С учетом найденных выше значений 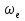 и и 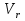 получаем при получаем при 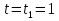 с: с: 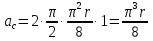 . .Вектор 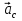 направлен согласно правилу векторного произведения, то есть перпендикулярно одновременно векторам направлен согласно правилу векторного произведения, то есть перпендикулярно одновременно векторам 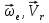 , в ту сторону, откуда поворот от , в ту сторону, откуда поворот от 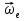 к к 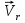 виден против хода часовой стрелки, то есть вдоль оси x вправо. виден против хода часовой стрелки, то есть вдоль оси x вправо.Модуль абсолютного ускорения точки М находим способом проекций: 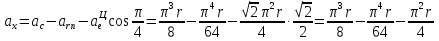 ; ;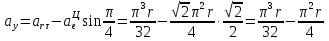 ; ; ; ;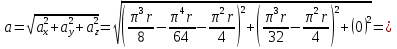 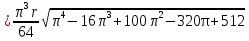 . .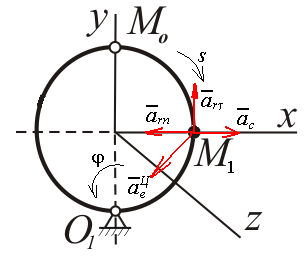 Ответ: 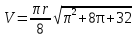 , , 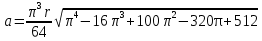 . .Расчётно-графическая работа на тему: «Динамическое исследование движения механической системы» Механическая система состоит из четырёх цилиндров, связанных между собой нерастяжимыми тросами. Каток 1 массы 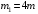 радиуса радиуса 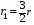 катится без скольжения по неподвижной плоскости, наклонённой под углом катится без скольжения по неподвижной плоскости, наклонённой под углом 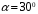 к горизонту. Блоки 2 и 3 – одинаковые сплошные однородные сдвоенные цилиндры массы к горизонту. Блоки 2 и 3 – одинаковые сплошные однородные сдвоенные цилиндры массы 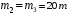 с внутренним радиусом с внутренним радиусом 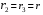 и наружным радиусом и наружным радиусом 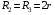 . Даны моменты инерции цилиндров: . Даны моменты инерции цилиндров: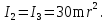 Система приводится в движение из состояния покоя моментом 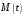 , приложенным к катку 1. , приложенным к катку 1.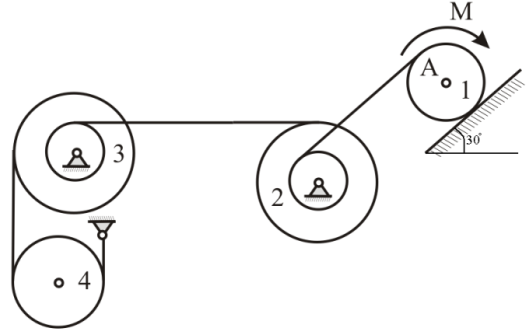 Исходные данные: 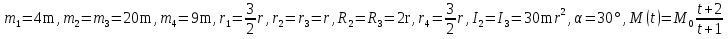 При выполнении задания необходимо:
Рассмотрим каток 1 и составим для него два уравнения, воспользовавшись двумя теоремами – теоремой о движении центра масс в проекции на ось 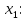 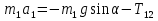 и теоремой об изменении кинетического момента: 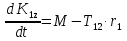 , где , где 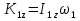 , , 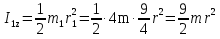 , то есть второе уравнение имеет вид , то есть второе уравнение имеет вид 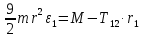 . .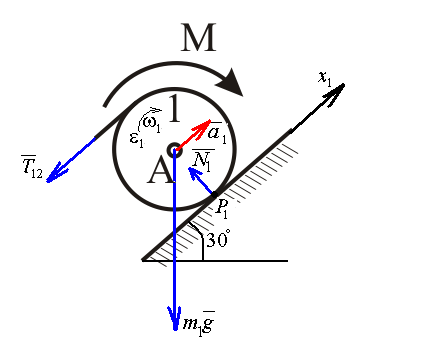 Рассмотрим цилиндр 2 и составим для него одно уравнение, используя теорему об изменении кинетического момента: 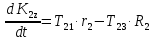 , где , где 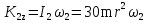 , то есть , то есть 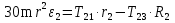 . .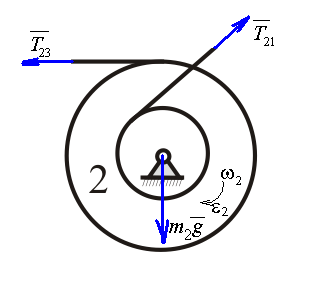 Рассмотрим цилиндр 3 и составим для него одно уравнение, используя теорему об изменении кинетического момента – 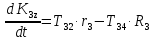 , где , где 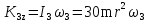 , то есть , то есть 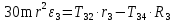 . .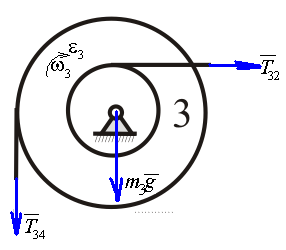 Рассмотрим цилиндр 4 и составим для него два уравнения, воспользовавшись двумя теоремами – теоремой о движении центра масс в проекции на ось 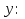 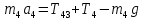 и теоремой об изменении кинетического момента: 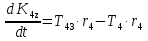 , где , где 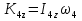 , , 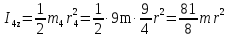 , то есть второе уравнение имеет вид , то есть второе уравнение имеет вид 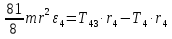 . .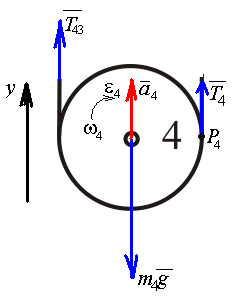 Таким образом, получили систему из 6 уравнений: 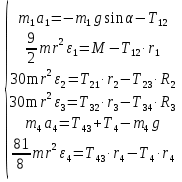 Исключим из этой системы уравнений внутренние силы и выразим все кинетические характеристики через ускорение центра масс катка 1 - 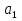 , воспользовавшись равенствами: , воспользовавшись равенствами: 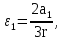 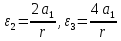 , ,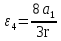 , , 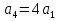 (подробнее о кинематических зависимостях написано в п.2 и п.3). При выводе уравнения использовали, что (подробнее о кинематических зависимостях написано в п.2 и п.3). При выводе уравнения использовали, что 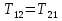 , , 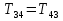 , , 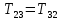 . В каждом уравнении выразили силы натяжения, а затем все уравнения сложили, в результате получили . В каждом уравнении выразили силы натяжения, а затем все уравнения сложили, в результате получили 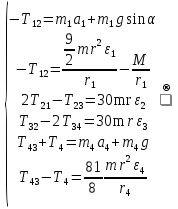 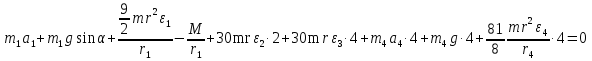 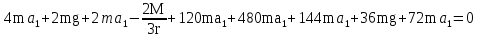 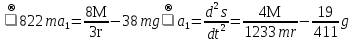 . .Получили дифференциальное уравнение второго порядка относительно S.
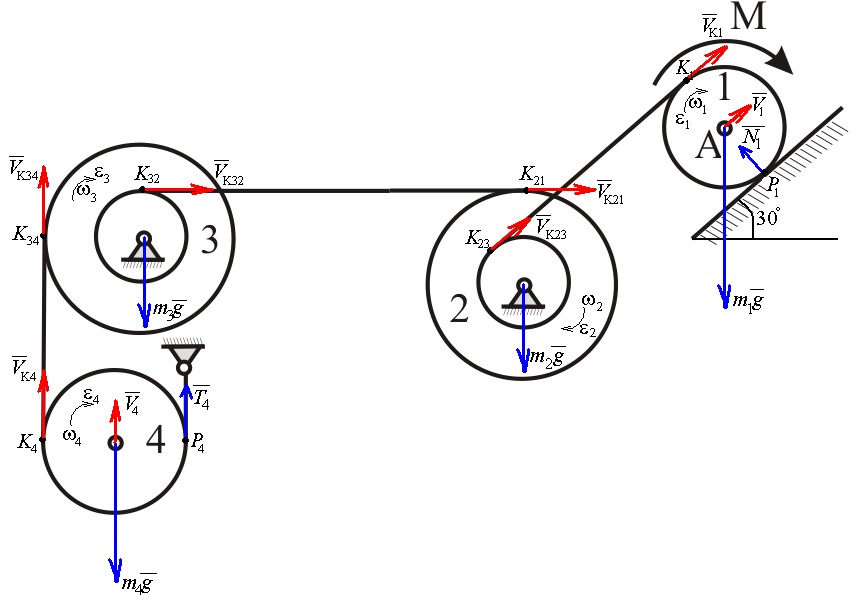 На систему действуют следующие внешние силы: силы тяжести 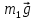 – катка 1, – катка 1, 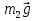 – блока 2, – блока 2, 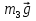 – блока 3 и – блока 3 и 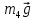 – цилиндра 4, – цилиндра 4, 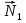 – нормальная реакция груза 1, сила натяжения троса – нормальная реакция груза 1, сила натяжения троса 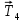 и вращающий момент и вращающий момент 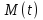 . .Применим теорему об изменении кинетической энергии механической системы в дифференциальной форме: 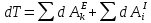 , где , где 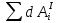 – сумма работ внутренних сил на элементарном перемещении (для этой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями: – сумма работ внутренних сил на элементарном перемещении (для этой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями: 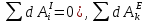 - сумма работ внешних сил на этом же перемещении, то есть - сумма работ внешних сил на этом же перемещении, то есть 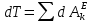 . .Кинетическая энергия системы равна: 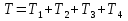 , где , где 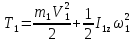 – кинетическая энергия катка 1, движущегося плоско-параллельно; – кинетическая энергия катка 1, движущегося плоско-параллельно; 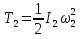 – кинетическая энергия цилиндра 2, вращающегося вокруг неподвижной оси; – кинетическая энергия цилиндра 2, вращающегося вокруг неподвижной оси; 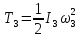 – кинетическая энергия цилиндра 3, вращающегося вокруг неподвижной оси; – кинетическая энергия цилиндра 3, вращающегося вокруг неподвижной оси; 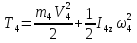 - кинетическая энергия цилиндра 4, движущегося плоско-параллельно. - кинетическая энергия цилиндра 4, движущегося плоско-параллельно.Таким образом, получаем 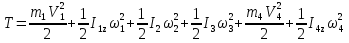 . .Выразим скорости центров масс и угловые скорости тел системы через линейную скорость катка 1 (составим уравнения связей). Мгновенный центр скоростей катка 1 находится в точке  , а мгновенный центр скоростей цилиндра 4 – в точке , а мгновенный центр скоростей цилиндра 4 – в точке 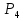 . Находим . Находим 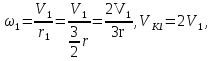 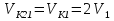 , но , но 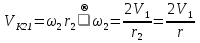 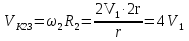 , , 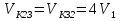 , , 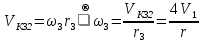 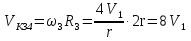 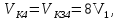 но но 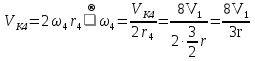 , ,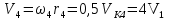 . .Учитывая исходные данные, имеем 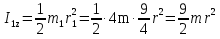 , ,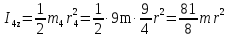 , ,Подставляя все в выражение для кинетической энергии, получаем: 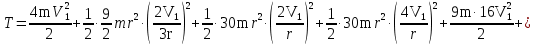 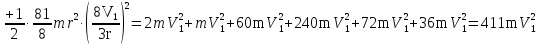 Найдем сумма элементарных работ внешних сил: 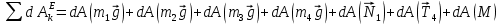 , ,где 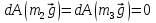 , так как точки приложения сил тяжести цилиндров 2 и 3 – неподвижны; , так как точки приложения сил тяжести цилиндров 2 и 3 – неподвижны; 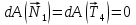 , так как эти силы приложены в мгновенных центрах скоростей соответствующих тел; , так как эти силы приложены в мгновенных центрах скоростей соответствующих тел; 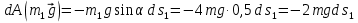 ; ; 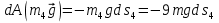 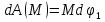 Так как соотношения между перемещениями, такие же как и между скоростями, то 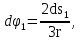 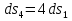 . .В результате получаем 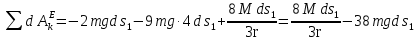 . .В итоге имеем следующее уравнение: 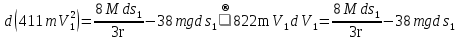 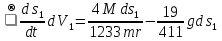 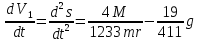 . .Получили дифференциальное уравнение второго порядка относительно S.
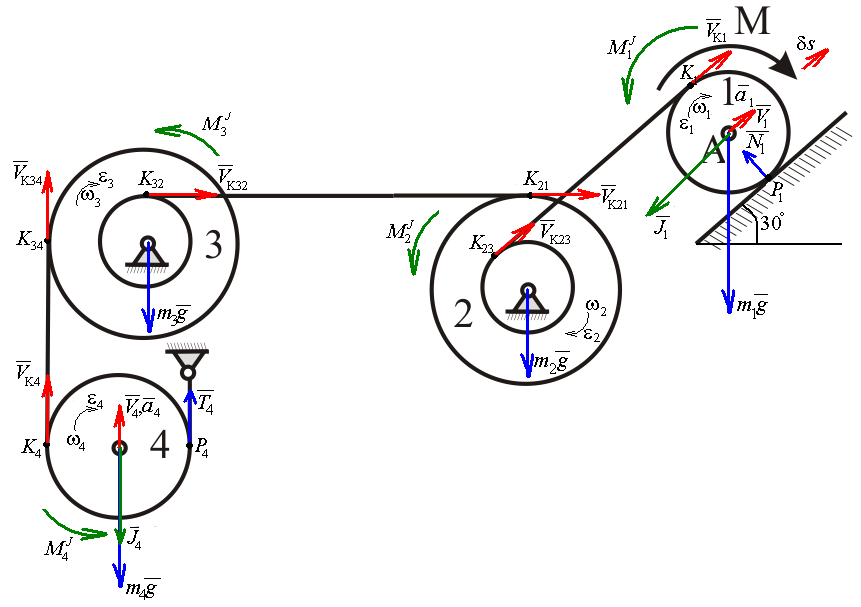 Так как система приходит в движение из состояния покоя, то направления ускорений тел соответствуют направлениям их движения. Будем считать, что движение системы таково, что каток 1 поднимается. Покажем внешние силы: силы тяжести 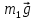 – катка 1, – катка 1, 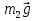 – блока 2, – блока 2, 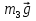 – блока 3 и – блока 3 и 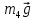 – цилиндра 4, – цилиндра 4, 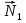 – нормальная реакция груза 1, сила натяжения троса – нормальная реакция груза 1, сила натяжения троса 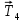 и вращающий момент и вращающий момент 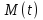 . .Приложим силы инерции. Сила инерции катка 1, совершающего плоско-параллельное движение, приводятся к вектору 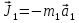 , где , где 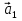 – ускорение центра масс катка 1 (точка А), и к паре сил, момент которой – ускорение центра масс катка 1 (точка А), и к паре сил, момент которой 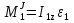 , где , где 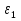 – угловое ускорение катка 1. – угловое ускорение катка 1.Силы инерции цилиндра 2, вращающегося вокруг неподвижной оси с угловым ускорением 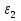 , приводятся к паре, момент которой , приводятся к паре, момент которой 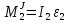 . .Силы инерции цилиндра 3, вращающегося вокруг неподвижной оси с угловым ускорением 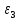 , приводятся к паре, момент которой , приводятся к паре, момент которой 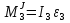 . .Сила инерции цилиндра 4, совершающего плоско-параллельное движение, приводятся к вектору 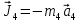 , где , где 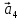 – ускорение центра масс цилиндра 4 (точка В), и к паре сил, момент которой – ускорение центра масс цилиндра 4 (точка В), и к паре сил, момент которой 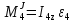 , где , где 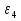 – угловое ускорение цилиндра 4. – угловое ускорение цилиндра 4.Сообщим системе возможное перемещение в направлении ее действительного движения. Составим общее уравнение динамики: 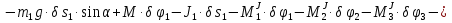 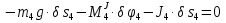 где 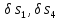 – линейные перемещения центров тяжести цилиндров 1 и 4, – линейные перемещения центров тяжести цилиндров 1 и 4, 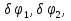 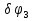 и и 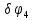 – углы поворотов цилиндров 1, 2, 3, 4. – углы поворотов цилиндров 1, 2, 3, 4.Зависимости между возможными перемещениями такие же, как и между соответствующими скоростями. Поэтому выразим скорости центров масс и угловые скорости тел системы через линейную скорость катка 1 (составим уравнения связей). Мгновенный центр скоростей катка 1 находится в точке 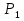 , а мгновенный центр скоростей цилиндра 4 – в точке , а мгновенный центр скоростей цилиндра 4 – в точке 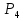 . .Находим 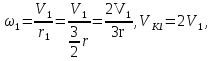 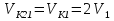 , но , но 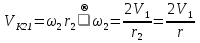 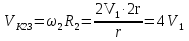 , , 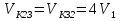 , , 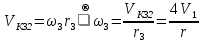 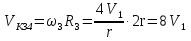 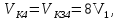 но но 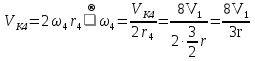 , ,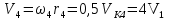 . .Такие же зависимости и между возможными перемещениями 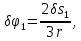 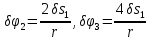 , ,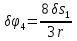 , , 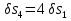 и между ускорениями 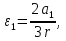 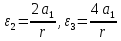 , ,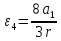 , , 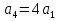 . .Таким образом, общее уравнение динамики принимает вид: 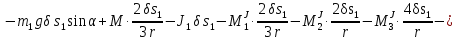 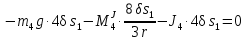 Учитывая исходные данные, имеем 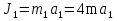 , , 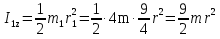 , ,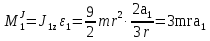 , , 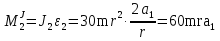 , ,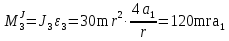 , ,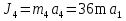 , , 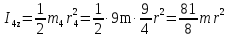 , ,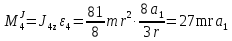 В результате общее уравнение динамики приобретает следующий вид: 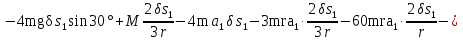 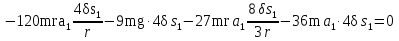 или 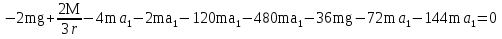 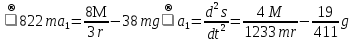 Получили дифференциальное уравнение второго порядка относительно s.
Данная механическая система имеет одну степень свободы, поэтому в качестве обобщенной координаты выберем перемещение центра масс катка 1, то есть 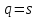 , тогда , тогда 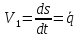 . Уравнение Лагранжа 2 рода имеет вид: . Уравнение Лагранжа 2 рода имеет вид: 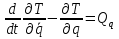 , где , где 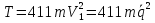 – кинетическая энергия системы, – кинетическая энергия системы, 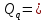 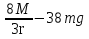 – обобщенная сила. – обобщенная сила.Таким образом, получаем 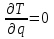 , , 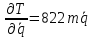 , , 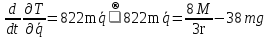 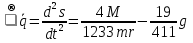 Получили дифференциальное уравнение второго порядка относительно s.
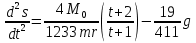 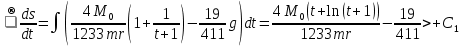 . .Так как система начинает двигаться из состояния покоя, то при 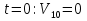 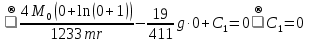 То есть 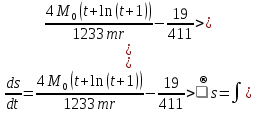  Так как при 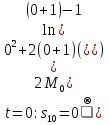 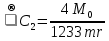 . .Таким образом, получили следующую зависимость координаты точки 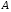 от времени от времени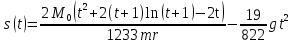
Построим график зависимости 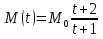 : :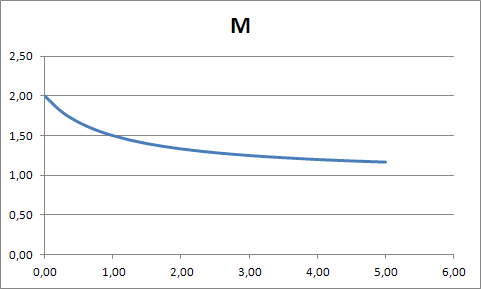 Построим график зависимости 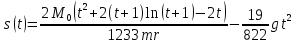 . .Данный график будет разным в зависимости от отношения 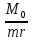 . .Если 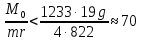 , то график имеет вид , то график имеет вид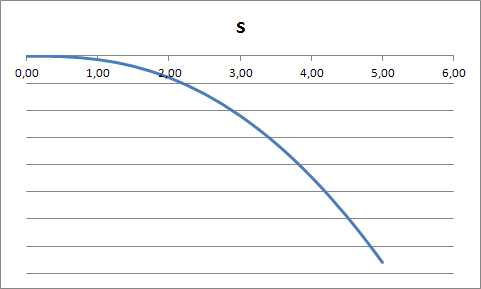 Если 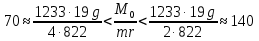 , то график имеет вид , то график имеет вид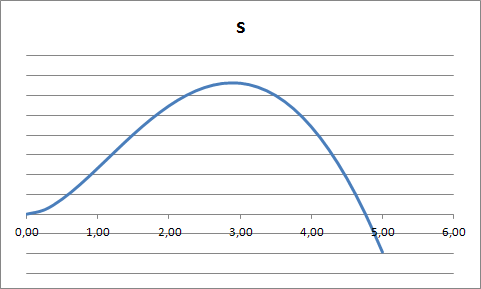 Причем чем ближе отношение 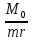 к 70, тем ближе вершина параболы к оси y и оси х, и тем больше график напоминаете предыдущий, а чем ближе отношение к 70, тем ближе вершина параболы к оси y и оси х, и тем больше график напоминаете предыдущий, а чем ближе отношение 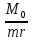 к 140, тем больше график напоминает тот, что расположен ниже. к 140, тем больше график напоминает тот, что расположен ниже.Если 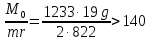 , то график имеет вид , то график имеет вид
При 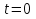 натяжения тросов найдем по формулам: натяжения тросов найдем по формулам: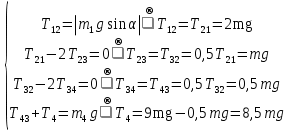 |

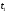 определить декартовы и дуговую координаты точки, вектор скорости, вектор ускорения и все его проекции. Полученные результаты изобразить на чертеже.
определить декартовы и дуговую координаты точки, вектор скорости, вектор ускорения и все его проекции. Полученные результаты изобразить на чертеже.