расчет внешне скоростной хар-ки. Пояснительная записка к курсовой работе Силовой, кинематический и динамический анализ плоскорычажного механизма по дисциплине Теория машин и механизмов
 Скачать 159.52 Kb. Скачать 159.52 Kb.
|
|
М  инОбрнауки РФ инОбрнауки РФСПбГАСУ  Автомобильно-дорожный факультет Кафедра наземных транспортно-технологических машин Пояснительная записка к курсовой работе «Силовой, кинематический и динамический анализ плоско-рычажного механизма» по дисциплине «Теория машин и механизмов»
Санкт-Петербург 2020 СодержаниеЗадание……………………………………………………………………………….4 1. Структурный анализ механизма …………………………………………………5 2. Построение планов положений механизма……………………………………..8 3. План скоростей …………………………………………………………………...9 4. План ускорений ………………………………………………………...…….….12 5. Силовой расчет механизма ………………………………………………..……15 6. Определение уравновешивающей силы метод Н.Е. Жуковского……...……..17 7.Определение реакций в кинематических парах………………………………..18 8. Определение момента инерции маховика…………………………………...…20 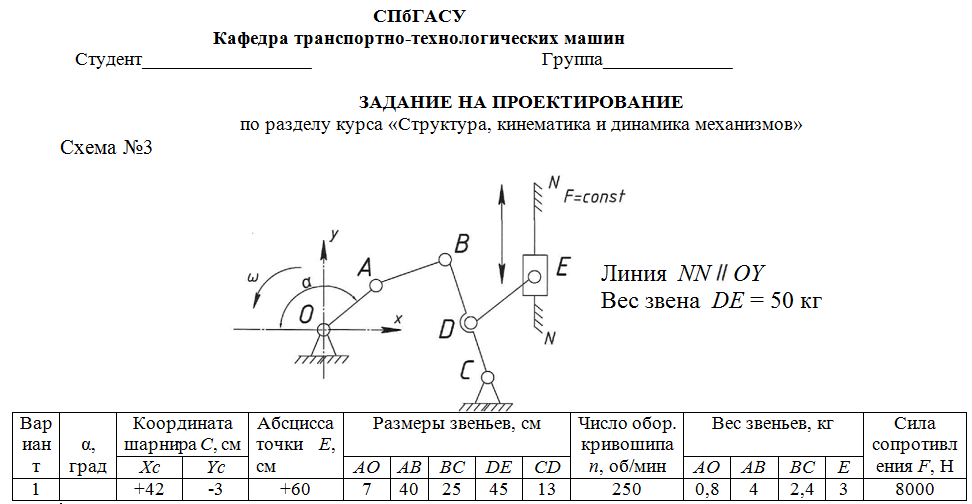 1. Структурный анализ механизмаСтруктурной особенностью данного механизма является наличие в его составе двукратного шарнира В. 1. Изображаем структурную схему заданного механизма. 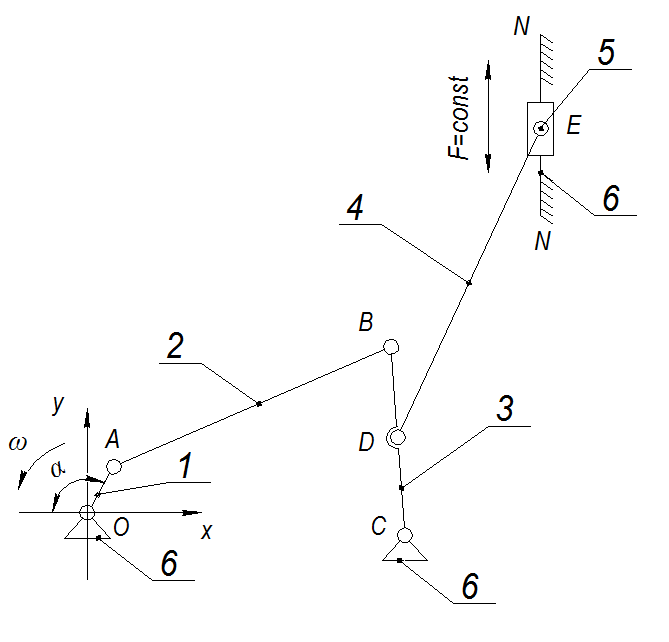 2. Мысленно приводя в движение звено 1, убеждаемся, что при этом все точки всех подвижных звеньев механизма двигаются только во взаимно параллельных плоскостях. Следовательно, этот механизм - плоский; 3. По результатам моделирования движения механизма охарактеризуем все звенья механизма и все кинематические пары. Исследуемый механизм имеет: число подвижных звеньев механизма 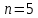 ; число низших кинематических пар ; число низших кинематических пар 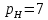 , (табл.1.1, 1.2). Высших кинематических пар , (табл.1.1, 1.2). Высших кинематических пар 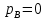 (в данном механизме их нет). (в данном механизме их нет).Следовательно, степень подвижности механизма равна: 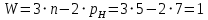 . .Это означает, что в рассматриваемом механизме достаточно задать закон движения только одному звену (в данном задании это звено 1, которое является ведущим), чтобы закон движения всех остальных звеньев был вполне определенным. 4. Из структурной схемы механизма выделяем начальный механизм - кривошип 1 со стойкой 6 и ведомую кинематическую цепь, содержащую все остальные звенья механизма. 5. Анализ ведомой кинематической цепи показывает, что она состоит из двух двухзвенных структурных групп, которые соединены между собой с помощью коромысла C. Группа 2-3 (ВВВ) и группа 4-5 (ВВП). Таблица 1.1 Характеристика звеньев механизма
Таблица 1.2 Характеристика кинематических пар
2. Построение планов положений механизмаПриняв на чертеже отрезок, изображающий длину кривошипа 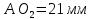 , определяем масштаб построения схемы механизма: , определяем масштаб построения схемы механизма: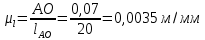 . .Длины остальных звеньев на чертеже: 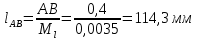 ; ; 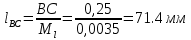 ; ; 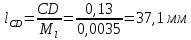 ; ; 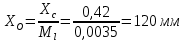 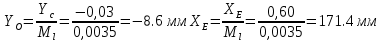 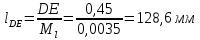 Методом засечек строим схему механизма для 6 равноотстоящих положений исходного звена AО. Строим ось размещения центра вращения кривошипа т. А, оси N - N перемещения ползуна E. Для построения планов положений звеньев, разделим траекторию, описываемую точной А кривошипа, на 6 равных частей. В качестве 0 принимаем то положение кривошипа, при котором ползун 5 находится в начале рабочего хода (крайнем правом положении), в качестве К (конечного) принимаем то положение кривошипа, при котором ползун 5 находится в конце рабочего хода (крайнем левом положении). Строим 6 равноотстоящих положений кривошипа по направлению его вращения. Из отмеченных на окружности точек 1, 2, 3, ..., 6 методом засечек строим 6 совмещенных положений механизма. Обозначим на звеньях положения их центров масс S, для исследуемого положения 1. Заданный механизм состоит из шести звеньев: 1- кривошип AО (ведущее, звено), движение вращательное; 2- шатун АВ, движение плоскопараллельное; 3- коромысло BD, движение вращательное; 4 - кулиса ED, движение плоскопараллельное; 5- ползун E, движение поступательное. 6- стойка, неподвижна. 3. Построение планов скоростей механизмаСкорость пальца т. А кривошипа, вращающегося с постоянной угловой скоростью: 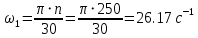 = const = constравна: 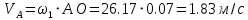 - const. - const.Из произвольно выбранного полюса плана скоростей Р проводим вектор ( 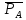 ) перпендикулярно АО в сторону ) перпендикулярно АО в сторону 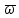 , изображающий , изображающий 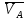 , длину которого принимаем , длину которого принимаем 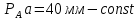 . . Масштаб плана скоростей: 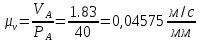 . .Скорости неподвижных точек О, C равны 0. на плане скоростей точки О, C совпадают с полюсом р. 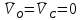 ; ; Определим скорость т. В, принадлежащей звеньям 2 и 3: 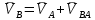 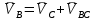 , ,где, 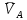 - скорость т. А, известна по модулю и направлена перпендикулярно звену АО2 в сторону вращения кривошипа; - скорость т. А, известна по модулю и направлена перпендикулярно звену АО2 в сторону вращения кривошипа;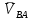 - скорость т. В при вращении шатуна вокруг т. А, перпендикулярна АВ, неизвестна по модулю (т. к. угловая скорость шатуна неизвестна). - скорость т. В при вращении шатуна вокруг т. А, перпендикулярна АВ, неизвестна по модулю (т. к. угловая скорость шатуна неизвестна).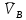 - скорость т. В, вращается со звеном 3 вокруг т. C, направлена перпендикулярно CB. - скорость т. В, вращается со звеном 3 вокруг т. C, направлена перпендикулярно CB.Решаем уравнение графически. Для этого из т. А проводим прямую, перпендикулярно звену АВ, до пересечения направлением 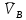 , которое проведено из полюса. В точке пересечения получаем точку b. , которое проведено из полюса. В точке пересечения получаем точку b. Модули скоростей из построения: 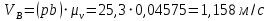 ; ;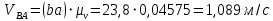 . .Определим скорость т. D, принадлежащей звеньям 4 и 5: 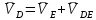 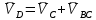 . .Так как т. D коромысла DB вращается вокруг т. С, то 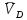 направлена обратно направлена обратно 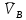 по перпендикуляру СD = перпендикуляру BC, таким образом, pd находится через отношение звеньев CD и BC коромысла DB: по перпендикуляру СD = перпендикуляру BC, таким образом, pd находится через отношение звеньев CD и BC коромысла DB: 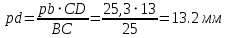 . .Модуль скорости: 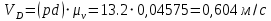 . .Определим скорость т. E, принадлежащей звеньям 4 и 5: 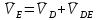 Решаем уравнение графически. Для этого из т. D проводим прямую, перпендикулярно звену DE, до пересечения X-X, которое проведено из полюса. В точке пересечения получаем точку E. Модули скоростей из построения: 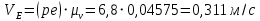 ; ;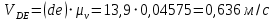 . .Результаты расчетов и построений сводим в таблицу 3.1 Таблица 3.1 Значение скоростей точек механизма
Проверим сходимость расчетной скорости для 2 положения ползуна E: 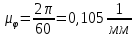 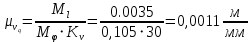 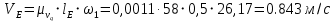 Определим относительную разницу между величинами 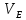 расчетной и расчетной и 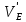 , полученной из графика: , полученной из графика:∆ 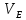 = =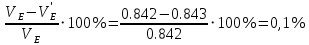 Полученная относительная разница ∆ 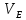 не превышает 10%, следовательно, результаты определения скоростей можно считать удовлетворительными. не превышает 10%, следовательно, результаты определения скоростей можно считать удовлетворительными. 4. Построение планов ускорений механизмаПолное ускорение т. А кривошипа складывается из нормального 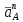 и тангенциального и тангенциального 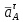 ускорений: ускорений: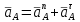 ; ;где 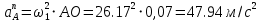 . .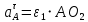 . .Т.к. по условию 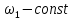 , тогда , тогда 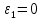 и и 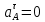 . .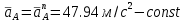 . .Принимаем длину вектора, изображающего 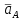 на плане ускорений на плане ускорений 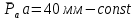 , тогда масштаб плана ускорений , тогда масштаб плана ускорений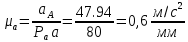 . .Из произвольно выбранного полюса плана ускорений Ра проводим вектор 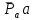 параллельно параллельно 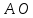 от А к О от А к О 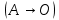 . . Ускорение т. В, принадлежащее звеньям 2 и 3: 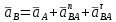 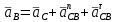 , ,здесь нормальные ускорения известны по направлению и величине: 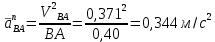 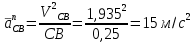 , ,отрезки, изображающие ускорения на плане ускорений: 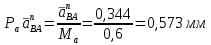 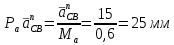 ; ;Решаем уравнение графически. Из т. A плана ускорений проведем отрезок 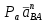 по линии действия вектора по линии действия вектора 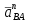 параллельно звену АВ. Вектор ускорения параллельно звену АВ. Вектор ускорения 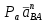 мал по величине и на чертеже свелся в точку. Далее проводим линию, перпендикулярную линии действия вектора мал по величине и на чертеже свелся в точку. Далее проводим линию, перпендикулярную линии действия вектора 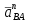 . Из полюса . Из полюса 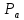 проведем отрезок проведем отрезок 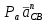 по линии действия вектора по линии действия вектора 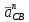 параллельно звену CB, а затем линию, перпендикулярную линии действия вектора параллельно звену CB, а затем линию, перпендикулярную линии действия вектора 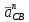 . На пересечении этих линий получим точку b. . На пересечении этих линий получим точку b.Ускорение т. D, принадлежащее звеньям 2 и 3: Так как т. D коромысла DB вращается вокруг т. С, то 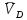 направлена обратно направлена обратно 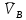 по перпендикуляру СD = перпендикуляру BC, таким образом, pd находится через отношение звеньев CD и BC коромысла DB: по перпендикуляру СD = перпендикуляру BC, таким образом, pd находится через отношение звеньев CD и BC коромысла DB: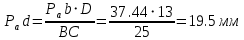 Ускорение т. E, принадлежащее звену 4: 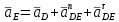 здесь нормальное ускорение известно по направлению и величине: 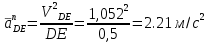 отрезок, изображающий ускорение на плане ускорений: 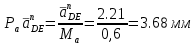 Решаем уравнение графически. Из т. D плана ускорений проведем отрезок 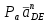 по линии действия вектора по линии действия вектора 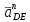 параллельно звену DE. Далее проводим линию, перпендикулярную линии действия вектора параллельно звену DE. Далее проводим линию, перпендикулярную линии действия вектора 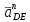 . Затем из полюса . Затем из полюса 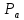 проведем линию действия проведем линию действия 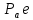 по линии X-X. На пересечении этих линий получим точку e. по линии X-X. На пересечении этих линий получим точку e.Модули ускорений из построения: 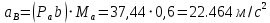 ; ;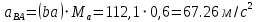 ; ;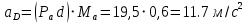 . .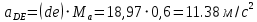 ; ;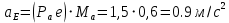 . .Результаты расчетов и построений сводим в таблицу 4.1 Таблица 4.1 — Значения ускорений точек и звеньев в положениях 2,3 .
Сходимость для 3 положения. 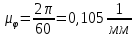 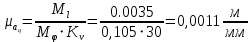 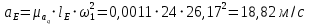 Определим относительную разницу между величинами 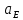 расчетной и расчетной и 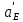 , полученной из графика: , полученной из графика:∆ 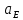 = =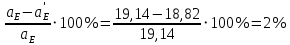 Полученная относительная разница ∆ 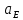 не превышает 10%, следовательно, результаты определения ускорений можно считать удовлетворительными. не превышает 10%, следовательно, результаты определения ускорений можно считать удовлетворительными.5. Силовой расчет механизма Будем проводить силовое исследование механизма для положения 3. Величина силы полезного сопротивления F=8000H Силы тяжести звеньев 1,2,3,4 и 5 определим по формуле: 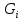 = = 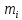 · g; · g;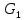 = 0,8 · 9.81 =7.85 H = 0,8 · 9.81 =7.85 H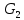 = 4· 9.81 = 39.24 H = 4· 9.81 = 39.24 H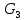 = 2,4 · 9.81 = 23.54H = 2,4 · 9.81 = 23.54H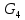 = 50 ·9.81 = 490.5 H = 50 ·9.81 = 490.5 H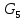 = 3 · 9.81 = 29.43 H = 3 · 9.81 = 29.43 H Центральные моменты инерции звеньев определяем по формуле: 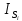 = = 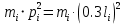 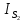 = 0.058 кг ·м2 = 0.058 кг ·м2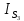 = 0.014 кг · м2 = 0.014 кг · м2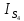 = 0.911 кг · м2 = 0.911 кг · м2Угловое ускорение: 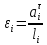 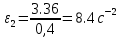 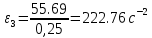 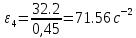 Главный момент сил инерции звеньев: 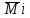 = - = -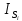 · Ɛ · Ɛ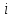 ; ;M 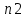 = -0.058· 8,4= -0.487 H ·м = -0.058· 8,4= -0.487 H ·мM 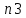 = -0.014 · 222,76 = -3.12 H · м = -0.014 · 222,76 = -3.12 H · мM 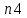 = -0.911 · 71,56= - 65.19 H · м = -0.911 · 71,56= - 65.19 H · м Главный момент сил инерции звеньев в масштабе: 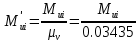 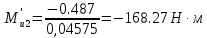 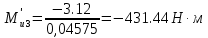 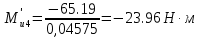 Главный вектор сил инерции проходит через цент масс S  Силы инерции звеньев: 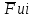 = - = -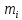 · · 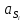 ; ;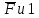 = 0 = 0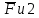 = -4 · 5.73= -22.92H = -4 · 5.73= -22.92H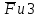 = -2,4 ·14.55= -34.92H = -2,4 ·14.55= -34.92H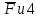 = -50 · 17.19= -859.5H = -50 · 17.19= -859.5H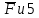 = -3 · 9.57= -28.71 H = -3 · 9.57= -28.71 H1) Упрощенный расчет приведенной силы 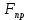 и приведенного момента и приведенного момента 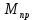 : :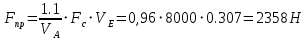 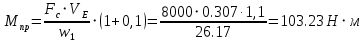 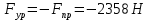 6. Определение уравновешивающей силы методом Н. Е.ЖуковскогоИзобразим на чертеже рычаг Жуковского, представляющий собой жесткую ферму, имеющую вид повернутого на 90 градусов (в любую сторону) плана скоростей механизма и закрепленного в полюсе. Масштаб построений: 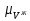 =0,0035 =0,0035 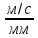 В соответствующие точки рычага Жуковского перенесем, сохраняя их направления все внешние силы и моменты, действующие на звенья механизма. Это: силы тяжести звеньев, главные векторы сил инерции, сил полезного сопротивления 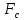 и главные моменты сил инерции звеньев: и главные моменты сил инерции звеньев:Определение уравновешивающей силы 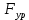 от действия сил тяжести и внешней силы с учетом сил инерции и моментов сил инерции. от действия сил тяжести и внешней силы с учетом сил инерции и моментов сил инерции.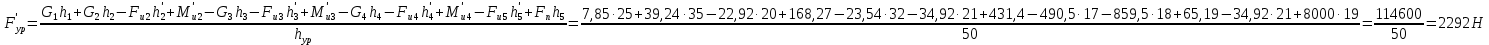 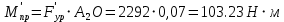 Определим относительную разницу между величинами 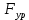 и и 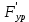 , найденными разными методами: , найденными разными методами: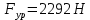 ∆F= 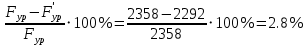 Полученная относительная разница ∆F не превышает 10%, следовательно, результаты определения уравновешивающей силы можно считать удовлетворительными. 7. Определение реакций в кинематических парахГруппа 4-5: Вычертим отдельно структурную группу 4-5 и покажем все силы, действующие на звенья данной группы. Отброшенные связи шатуна 4 с коромыслом 3 и ползуна с направляющей заменим реакциями R34 и R56 R34 = 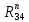 + +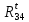 где где 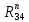 параллельно DE, а параллельно DE, а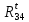 перпендикуляр DE. R56 перпендикулярно N-N перпендикуляр DE. R56 перпендикулярно N-NРассмотрим равновесие звена 4 относительно внутреннего шарнира группы E, плечи сил измеряем на чертеже: ∑МE =- 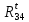 · · 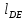 + Mи4 -G4 · h -Fи4 · + Mи4 -G4 · h -Fи4 · 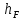 = 0 = 0 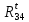 = = 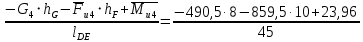 =-15.62 H =-15.62 HИз общего условия равновесия группы 4-5 ∑F=0; 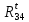 +G4 + Fи4+ G5 + Fи5 + F + R56+ +G4 + Fи4+ G5 + Fи5 + F + R56+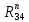 = 0 = 0 По этому векторному уравнению строим план сил группы 4-5 в масштабе: MF = 150 H/мм Из построения определяем искомые реакции, замыкающие план сил: R34 = 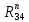 · MR3= 58.7 · 150 = 8805 H · MR3= 58.7 · 150 = 8805 HR5 = 24.5 ·150 = 3675 H Группа 2-3 Вычертим отдельно структурную группу 2-3 и покажем все силы, действующие на звенья данной группы. Отброшенные связи с кривошипом и шатуном ползуна заменим реакциями R12 и R63 R12 = 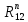 + +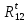 где где 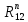 параллельно AB, параллельно AB, 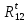 перпендикулярно АВ перпендикулярно АВДействие отброшенного шатуна 4 заменим реакцией R43 = -R34 = -8805 H Рассмотрим равновесие звена 3 относительно внутреннего шарнира группы C, плечи сил измеряем на чертеже: Для звена 3: ∑MB= R34· hr34 +Mи3 -G3 · h3 + Fи3 · hu3 + 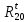 · BC= 0 · BC= 0 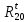 = =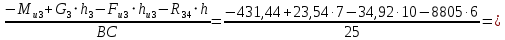 12083 Н 12083 НДля звена 2: ∑MB= 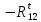 · hr12+ Mи2 +G2 · h2 - Fи2 · hu2 = 0 · hr12+ Mи2 +G2 · h2 - Fи2 · hu2 = 0 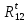 = =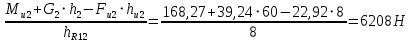 Из общего условия равновесия группы 2-3 ∑Fi= 0; R43 + G3 + Fи3 + R20 + G2 + Fи2 + 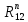 + + 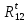 = 0 = 0 По этому векторному уравнению строим план сил группы 2-3 в масштабе: 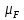 = 150 H/мм = 150 H/ммИз построения определяем реакции, замыкающие план сил: 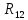 = 87.5· 150 = 13125 H = 87.5· 150 = 13125 HНачальное звено: Вычертим отдельно начальное звено 1 и покажем все действующие силы. Отброшенные связи кривошипа со стойкой заменим реакцией R61, действие отброшенного шатуна 2 заменим реакцией R21 = -R12 = -13125H ∑MO2= 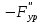 · AO2 –R12 · h - G1 · h1 = 0 · AO2 –R12 · h - G1 · h1 = 0 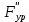 = =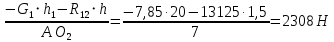 Определим относительную разницу между величинами 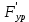 и и 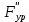 , найденными разными методами: , найденными разными методами:∆F= 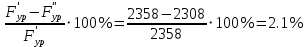 Полученная относительная разница ∆F не превышает 5%, следовательно, результаты определения уравновешивающей силы можно считать удовлетворительными. 8. Определение момента инерции маховика1.Приведенный момент маховика для 6 положений механизма: 1) 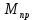 = =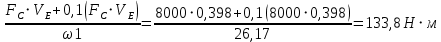 2) 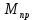 = =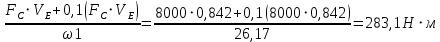 3) 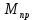 = =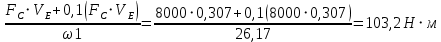 4) 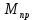 = =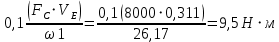 5) 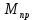 = =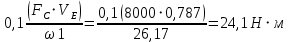 6) 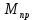 = =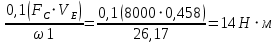 2.Построим диаграмму в вычислительном масштабе: 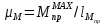 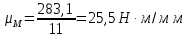 3.Графически проинтегрируем эту диаграмму 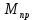 и построим диаграмму работы сил сопротивления Ас и построим диаграмму работы сил сопротивления Ас4.Определим момент инерции маховика 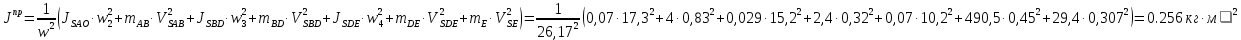 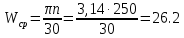 5. Используя величину 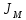 определим вес и геометрические размеры маховика: определим вес и геометрические размеры маховика: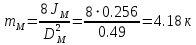 г г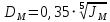 =0,35·2.01=0.7 м =0,35·2.01=0.7 мШирина обода маховика: 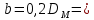 0,2·0,7=0,14 м 0,2·0,7=0,14 м | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
