Камилжан С.Д. Кинематика и динамика материальной точ. Кинематика и динамика материальной точки. Динамика твердого тела

• Название: Кинематика и динамика материальной точки. Динамика твердого тела
• Дата: 05.12.2021
• Размер: 0.57 Mb.
• Имя файла: Камилжан С.Д. Кинематика и динамика материальной точ.docx
• Тип: Реферат; #292387
• страница: 2 из 4

). Сама эта точка называется центром силы, или силовым центром. Примером центральных сил являются гравитационные силы, силы электростатического взаимодействия.


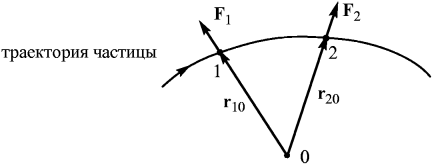Рис. 3. Точка 0 - силовой центр. Силы F1(r10) и F2(r20) зависят только от расстояния до центра.
Примером таких сил также могут служить силы гравитационного притяжения Земли к Солнцу (или Луны к Земле).

Покажем, что работа центральных сил также не зависит от формы пути и определяется только начальным и конечным положениями материальной точки. Для этого произведем бесконечно малое перемещение dr.

При этом |dr|cosα = dr, где dr - приращение расстояния до центра. Таким образом, dA = Fdr и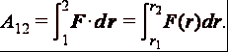

(15)
Значение определенного интеграла зависит только от нижнего и верхнего пределов r₁ и r₂ и, таким образом, не зависит от формы пути.

Материальная точка, движущаяся в поле центральных сил, представляет собой консервативную систему. Поэтому при движении материальной точки сохраняется и полная механическая энергия точки, т.е.
.
Для центрального гравитационного поля большой массы М имеем
.
Законы Кеплера

В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.

Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.

Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации - открытию закона всемирного тяготения.

Первый закон Кеплера:

Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

На рис. 4 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца, называется афелием или апогеем. Расстояние между афелием и перигелием - большая ось эллипса.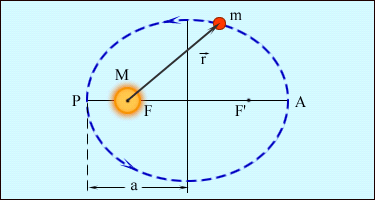


Рисунок 4
Эллиптическая орбита планеты массой m << M. а - длина большой полуоси, F и F' - фокусы орбиты.

Второй закон Кеплера:

Радиус-вектор планеты описывает в равные промежутки времени равные площади.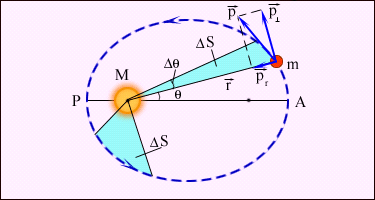


Рисунок 5
Закон площадей - второй закон Кеплера.

Второй закон Кеплера эквивалентен закону сохранения момента импульса На рис. 5 изображен вектор импульса тела и его с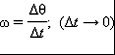оставляющие и Площадь, заметенная радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:

Здесь - угловая скорость

Момент импульса L по абсолютной величине равен произведению модулей векторов и


Из этих отношений следует:

Поэтому, если по второму закону Кеплера то и момент импульса L при движении остается неизменным.

В частности, поскольку скорости планеты в перигелии и афелии направлены перпендикулярно радиус-векторам и из закона сохранения момента импульса следует:
rPυP = rAυA.

Третий закон Кеплера:

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит: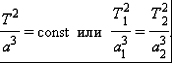

5. Закон сохранения энергии
Границы движения

Закон сохранения энергии разрешает анализировать характер движения.

Рассмотрим одномерное движение. Запишем Закон сохранения энергии:

Кинетическая энергия всегда позитивна, поэтому потенциальная энергия никогда не может быть больше полной:

Следовательно, частичка может находиться только в тех точках пространства, где ее потенциальная энергия не превышает полную.

Т.е. существуют границы движения.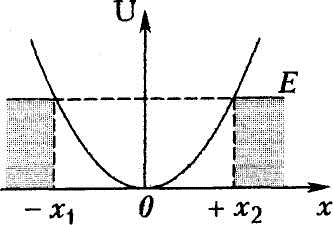


Пример 1. Пусть потенциальная энергия зависит от координаты по закону квадратичной параболы (рис. 6):

Если E_n - полная энергия, а частица не может владеть потенциальной энергией больше полной, то это значит, что она может двигаться в границах от -х₁ до +х₂. заштрихованные на рисунке области запрещены для движения частиц. В этих областях потенциальная энергия больше полной. Для проникновения в запрещенные зоны частица должна получить дополнительную полную энергию.

Пример 2. Рассмотрим более сложный вид потенциальной кривой (рис. 7). Помимо потенциальной ямы тут присутствует потенциальный барьер (от х₃ до х₅).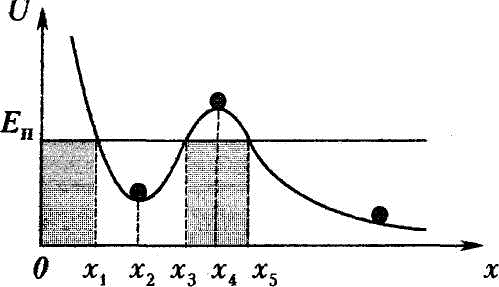

Выберем полную энергию таковой, чтоб она была меньше максимума потенциального барьера, но большей минимума потенциальной ямы.

Как и раньше, области, где потенциальная энергия больше полной, недоступны для движения частицы. Первая область: от 0 до х₁, вторая:х₃ до х₅. В области от х₁ до х₃

В области от х₅ до бесконечности потенциальная энергия меньше полной и движение здесь дозволено. Такое движение называется инфинитным или неограниченным.

Шарик в таком желобе может выполнять колебания в потенциальной яме, либо покатиться в бесконечность, если уже находится правее потенциального барьера. Для того чтобы преодолеть барьер, шарик должен обладать полной энергией, большей потенциального барьера. В противном случае говорят, что частица не может преодолеть потенциальный барьер.

Удар абсолютно упругих и неупругих тел

Ударом (столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин. В процессе удара возникают кратковременные ударные силы взаимодействия между сталкивающимися телами, причем эти силы во много раз превосходят все внешние силы, действующие на тела. Поэтому в процессе удара систему соударяющихся тел можно приближенно считать замкнутой и применять к ней закон сохранения импульса.

В механике часто используются две модели ударного взаимодействия - абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

При абсолютно неупругом ударе, нижеприведенная формула позволяет найти скорость центра масс соединившихся при ударе тел. Однако в результате такого удара может также возникнуть вращение системы вокруг ее центра масс, согласующееся с законом сохранения момента импульса.

При неупругом ударе происходят различного рода процессы в соударяющихся телах (их пластические деформации, трение и др.), в результате которых кинетическая энергия системы частично преобразуется в ее внутреннюю энергию, т. е. происходит диссипация механической энергии системы.

Изменение кинетической энергии системы двух сталкивающихся тел при абсолютно неупругом прямом ударе равно: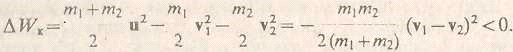

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел механическая энергия соударяющихся тел не преобразуется в другие виды энергии.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.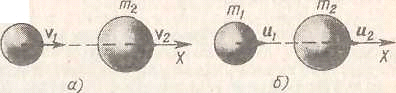

Пусть два абсолютно упругих шара массами m₁ и m₂ движутся до удара поступательно со скоростями ; и направленными вдоль оси ОХ, проходящей через центры шаров. Нужно найти скорости и,U₁ и U₂; шаров после соударения

В процессе удара систему соударяющихся упругих тел можно считать замкнутой и консервативной. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, так что потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем:

По закону сохранения импульса:

Так как все скорости направлены по оси ОХ, то:

где -проекции векторов на линию удара - ось ОХ. Так как , то мы имеем:

Совместное решение уравнений дает:

Окончательно получаем:

Условия равновесия тела:

1. Закон сохранения механической энергии позволяет указать условия равновесия консервативных систем. Состоянием механического равновесия называется такое состояние системы, из которого она может быть выведена только в результате внешнего силового воздействия. В этом состоянии все материальные точки системы находятся в покое, так что кинетическая энергия системы равна нулю. Состояние механического равновесия системы называется устойчивым, если малое внешнее воздействие на систему вызывает малое изменение ее состояния. При этом в системе возникают силы, стремящиеся возвратить ее в состояние равновесия. Состояние механического равновесия называется неустойчивым, если система при сколь угодно малом внешнем воздействии выходит из этого состояния и больше не возвращается в него. При этом возникают силы, вызывающие дальнейшее отклонение системы от состояния равновесия. Согласно закону сохранения механической энергии, в состояниях устойчивого равновесия потенциальная энергия системы имеет минимумы, а в состояниях неустойчивого равновесия - максимумы.

2. Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

3. Частица находится в состоянии равновесия в тех точках пространства, где ее потенциальная энергия минимальна либо максимальна.

4. Тело находится в равновесии, если оно не обладает ускорением поступательного и вращательного движений. Очевидно, что это имеет место при равенстве нулю результирующей силы и суммарного момента внешних сил. Следовательно, в условии равновесия выполняются равенства: F = 0 и M = 0.

. Неинерциальные системы отсчета

Вес и невесомость

Силу тяжести с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни.

Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Пусть тело лежит на неподвижном относительно Земли горизонтальном столе (рис. 8). Систему отсчета, связанную с Землей, будем считать инерциальной. На тело действуют сила тяжести направленная вертикально вниз, и сила упругости с которой опора действует на тело. Силу называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга: В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой равной по модулю силе реакции опоры и направленной в противоположную сторону: