Метрология. Класс точности (В 4). Классы точности средств измерений

• Название: Классы точности средств измерений
• Анкор: Метрология
• Дата: 24.02.2023
• Размер: 126.03 Kb.
• Имя файла: Класс точности (В 4).docx
• Тип: Практическая работа; #952815

Практическая работа

КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

Цель занятия: получить практические навыки решения задач на вычисление погрешностей при различных способах задания классов точности приборов.

Задание. Решить задачи, номера которых приведены в таблице 4, согласно полученному варианту.
Задача 1. Вольтметром класса точности 0.2 со шкалой (0…100) В измерены значения напряжения 0; 10; 20; 40; 50; 60; 80; 100 В. Рассчитать зависимости абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение:
Для записи результатов формируем таблицу 1, в столбцы которой будем записывать измеренные значения V, абсолютные ΔV, относительные δV погрешности и приведённые γV погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 В.

Класс точности амперметра задан числом без кружка, следовательно, приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т. е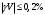

При решении задачи рассмотрим худший случай 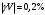когда приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует и

Данные значения приведённой погрешности заносим в четвёртый столбец таблицы 1.

Рассчитаем значения абсолютной погрешности.

Из формулы 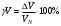выражаем абсолютную погрешность

За нормирующее значение принимаем размах шкалы, так как шкала вольтметра содержит нулевую отметку, т.е.

Абсолютная погрешность 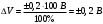во всех точках шкалы прибора.

Заносим данное значение во второй столбец таблицы.
Таблица 1 – Результаты расчёта значений погрешностей

V, B	ΔV, B	δV, %	γV, %
0	± 0,2	± ∞	± 0,2
10	± 0,2	± 2	± 0,2
20	± 0,2	± 1	± 0,2
40	± 0,2	± 0,5	± 0,2
50	± 0,2	± 0,4	± 0,2
60	± 0,2	± 0,33	± 0,2
80	± 0,2	± 0,25	± 0,2
100	± 0,2	± 0,2	± 0,2

Значения относительной погрешности будем рассчитывать по формуле
При V = 0 B получаем

При V = 1 B получаем

Значения относительной погрешности для остальных измеренных значений тока рассчитываются аналогично. Полученные таким образом значения относительной погрешности заносим в третий столбец.

По данным таблицы 1 строим графики зависимостей абсолютной ΔV, относительной δV и приведенной γV погрешностей от результата измерений V (см. рис. 1).




Рис. 1 – Графики зависимостей абсолютной, относительной и приведенной погрешностей от результата измерений

Задача 2. Амперметром класса точности со шкалой (0…10) А измерены значения тока 0; 1; 1,5; 4; 5; 6; 9; 10 А. Рассчитать зависимости абсолютной и относительной погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение. Для записи результатов формируем таблицу 2, в столбцы которой будем записывать измеренные значения I, абсолютные ΔI и относительные δI погрешности.
Таблица 2 – Результаты расчёта значений погрешностей

I, A	ΔI, A	δI, %
0	0	1,5
1	0,015	1,5
1,5	0,0225	1,5
4	0,06	1,5
5	0,075	1,5
6	0,09	1,5
9	0,135	1,5
10	0,15	1,5

В первый столбец записываем заданные в условии задачи измеренные значения тока: 0; 1; 1,5; 4; 5; 6; 9; 10 А. Класс точности амперметра задан числом в кружке, следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е.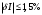

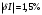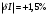При решении задачи рассмотрим худший случай, т.е. , что соответствует значениям и

Значение относительной погрешности столбец таблицы. I 1,5 % заносим в третий.

Рассчитаем значения абсолютной погрешности.

Из формулы 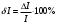выражаем абсолютную погрешность:
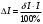При I = 0 A получаем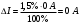
При I = 1 A получаем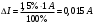

Значения абсолютной погрешности для остальных измеренных значений трка рассчитываются аналогично. Полученные таким образом значения абсолютной погрешности заносим во второй столбец.

По данным таблицы 2, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной ΔI и относительной δI погрешностей от результата измерений I.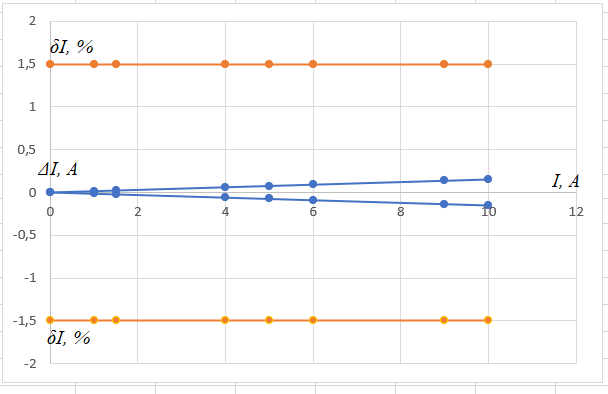

Рис. 2 – Графики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с преобладающими мультипликативными погрешностями


Задача 3. Цифровым термометром класса точности 0.5/0.25 со шкалой

(-100...+100) ⁰С измерены значения температуры 0; 10; 20; 40; 50; 60; 90; 100 ⁰С. Рассчитать зависимости абсолютной и относительной основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение. Для записи результатов формируем таблицу 3, в столбцы которой будем записывать измеренные значения T, абсолютные ΔT и относительные δT погрешности.

В первый столбец записываем заданные в условии задачи измеренные значения температуры 0; 10; 20; 40; 50; 60; 90; 100 ⁰С.
Таблица 3 – Результаты расчёта значений погрешностей

Т, 0С	Δ Т, 0С	δТ, %
0	0,25	∞
10	0,275	2,75
20	0,3	1,5
40	0,35	0,875
50	0,375	0,75
60	0,4	0,667
90	0,475	0,528
100	0,5	0,5

Класс точности термометра задан в виде двух чисел, разделённых косой чертой. Следовательно, относительная погрешность, выраженная в процентах, во всех точках шкалы должна удовлетворять следующему соотношению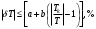


В данном случае а = 0.5; b= 0.25; T_k = 100 ⁰С, причём параметры этой формулы а и b определяются мультипликативной и аддитивной составляющими суммарной погрешности соответственно. Таким образом, получаем

При решении задачи рассмотрим худший случай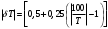

что соответствует значениям

Рассчитаем значения относительной погрешности:
При Т = 0 ⁰С получаем

При Т = 10 ⁰С получаем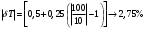

Значения относительной погрешности для остальных измеренных значений сопротивления рассчитываются аналогично.

Полученные значения относительной погрешности заносим в третий столбец таблицы 3.

Рассчитаем значения абсолютной погрешности.
Из формулы выражаем абсолютную погрешность: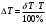
При Т = 0 ⁰С получаем - неопределенность

Искомое значение ΔТ можно определить следующим образом. Так как класс точности прибора задан в виде двух чисел, то у данного прибора аддитивные и мультипликативные погрешности соизмеримы. При Т = 0 ⁰С мультипликативная составляющая погрешность равна нулю, значит, общая погрешность в этой точке обусловлена только аддитивной составляющей.

Аддитивную составляющую представляет второе из чисел, задающих класс точности, т.е. в данном случае число b = 0.25. Это означает, что аддитивная погрешность составляет 0,05 % от верхнего предела измерений прибора, т.е. от T_k = 100 ⁰С.
Таким образом, при T = 0 ⁰С имеем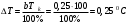

при T = 10 ⁰С имеем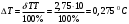

при T = 20 ⁰С имеем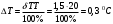

Значения абсолютной погрешности для остальных измеренных значений сопротивления рассчитываются аналогично. Полученные таким образом значения абсолютной погрешности заносим во второй столбец таблицы 3.

По данным таблицы 3, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной ΔT и относительной δT погрешностей от результата измерений T.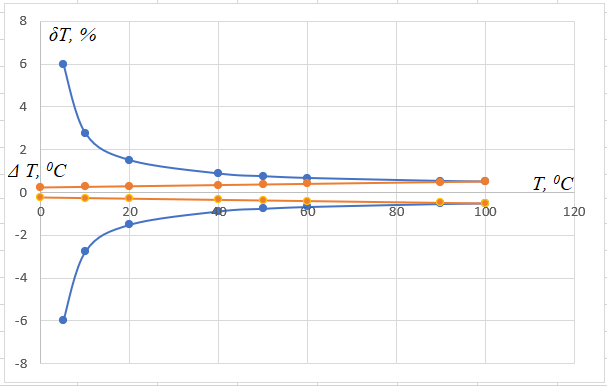

Рис. 3 – Графики зависимостей абсолютной и относительной погрешностей от результата измерений для прибора с соизмеримыми аддитивными и мультипликативными погрешностями