лекция теория вероятностей. лекция по ТВ. Классическая вероятностная модель Геометрическая вероятность

• Название: Классическая вероятностная модель Геометрическая вероятность
• Анкор: лекция теория вероятностей
• Дата: 05.12.2022
• Размер: 0.67 Mb.
• Имя файла: лекция по ТВ.doc
• Тип: Глава; #829159

Глава 2. Классическая вероятностная модель

Геометрическая вероятность
§ 1. Пространство элементарных исходов.
Каждый эксперимент заканчивается каким-то определенным результатом, который не всегда возможно заранее предугадать. Для того, чтобы формально описать некоторый эксперимент, нужно указать все возможные варианты результатов, которыми этот эксперимент может закончиться. В теории вероятностей такие результаты называются исходами. Множество  всех возможных исходов эксперимента называется пространством элементарных исходов. Предполагается, что эксперимент может закончиться одним и только одним элементарным исходом. В наиболее простом случае все эти исходы можно перечислить:

 = ₁ , ₂, ... _n, или = ₁, ₂ , ....

Такое пространство элементарных исходов называется дискретным.

Простейшим пространством элементарных исходов является такое пространство, в котором все указанные исходы рассматриваемого эксперимента

1. 
   равновозможны;
   
2. 
   взаимно несовместны (т.е. в результате эксперимента может произойти один и только один из указанных исходов),
   
3. 
   все исходы образуют полную группу событий (т.е . никакие другие исходы, кроме перечисленных, не могут произойти).
   

Такое пространство конечно и называется пространством равновозможных исходов (или симметричным пространством).
ПРИМЕР 1. При бросании симметричной монеты возможны два исхода – выпадение решки или герба. Они удовлетворяют всем трем указанным выше условиям и потому в этом случае пространство элементарных исходов представляется так (здесь буквами Р и Г обозначены решка и герб соответственно):


ПРИМЕР 2. При одновременном бросании двух монет исходы представляют собой упорядоченные пары, состоящих из символов Р и Г. Первый элемент этой пары – результат, выпавший на первой монете, второй элемент – результат на второй монете. Очевидно, что таких пар – четыре:


ПРИМЕР 3. В случае бросания игральной кости может выпасть любое из чисел 1, 2, 3, 4, 5, 6. Поэтому пространство элементарных исходов
ПРИМЕР 4. При одновременном бросании двух игральных костей элементарные исходы представляют собой пары (x, y), где x – число очков, выпавшее на первой кости, а y – число очков на второй кости. Всего таких пар – 36:


§ 2. Событие и его вероятность.
В дискретном пространстве вероятность каждого элементарного исхода считается заданной и обозначается Р(_i), или просто р_i , причем всегда

1. 
   р_i  0
   
2. 
   (или ),
   

т.е. сумма (конечная или бесконечная) вероятностей всех элементарных исходов равна единице. Элементарные исходы мы называем элементарным событием.

Событием называется любое подмножество, состоящее из элементарных исходов пространства элементарных событий . Говорят, что «событие А произошло», если эксперимент закончился одним из элементарных исходов _iА.

Вероятностью события А называется сумма вероятностей всех элементарных исходов, входящих в А, то есть Р(А)= . Из этого определения вероятности события следует, что всегда 0  Р(А)  1.

В случае равновозможных исходов вероятность элементарного события А определяется формулой

,

где – число элементов во множестве , которое обычно называется «общее число исходов», а – число элементов во множестве A, называемое «числом благоприятствующих исходов».

Событие А, состоящее из всех элементарных исходов, не входящих в А, называется противоположным событием к событию А. Оно происходит тогда и только тогда, когда событие A не произошло. Очевидно что Р(А) + Р(А) = 1. Это равенство используется для вычисления вероятности события А в случае, когда вероятность противоположного события известна или легко может быть найдена, тогда Р(А) = 1 - Р(А).

Таким образом, для вычисления вероятности в каждой задаче важно определить, в чем состоит эксперимент, правильно построить соответствующее пространство элементарных событий  и выделить в нем требуемое событие A. Затем, используя методы комбинаторики, подсчитать число элементов в  и A.
Задача 1. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?

Решение. Элементарными исходами здесь являются выборки, включающие 3 фрукта.

Решение. Так как порядок здесь безразличен, будем считать выборки неупорядоченными (и, разумеется, бесповторными). Общее число элементарных исходов 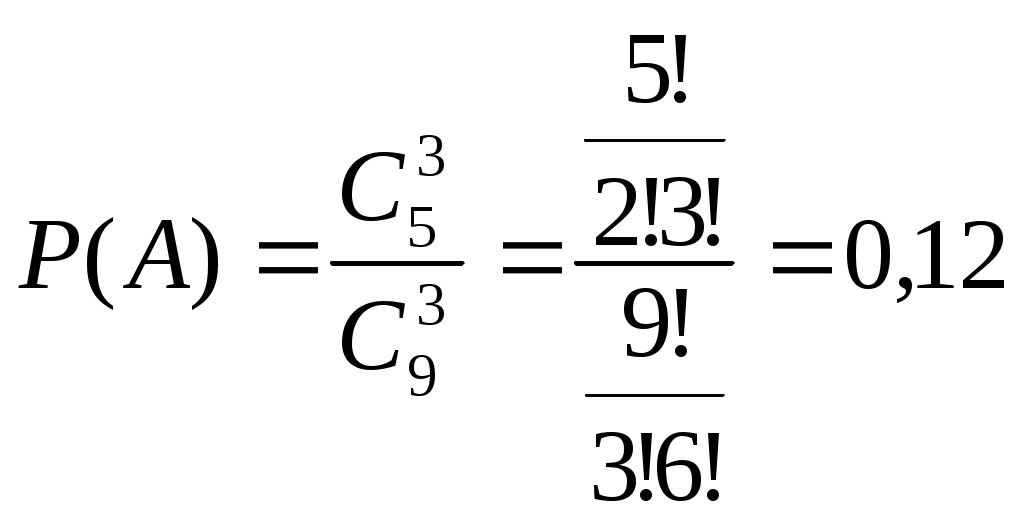равно числу способов выбрать 3 элемента из 9, т.е. числу сочетаний n= . Число благоприятных исходов m= будет равно числу способов выбора трех апельсинов из имеющихся 5, т.е. числу сочетаний трех элементов из 5, т.е. . Тогда вероятность

.
Задача 2. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманы числа совпадут.

Решение. Подсчитаем сначала общее количество исходов. Элементарными исходами будем считать упорядоченные совокупности задуманных чисел: N₁, N₂, N₃, где N₁ - число, задуманное первым студентом, N₂ - вторым и N₃ - третьим Первый из них выбирает одно из 10 чисел — 10 возможностей, второй делает то же самое — 10 возможностей, наконец, выбор третьего также 10 возможностей. Согласно основной теоремы комбинаторики общее число способов будет равно:

n= N₁N₂N₃=10³ = 1000 элементарных исходов.

Подсчет количества благоприятных исходов более сложен. Заметим, что совпадение задуманных чисел может произойти у любой пары студентов (или даже одновременно у всех троих). Чтобы не разбирать отдельно все эти случаи, удобно перейти к противоположному событию, т.е. подсчитать количество тех случаев, когда все три студента задумывают разные числа. Первый из них по-прежнему имеет 10 способов выбора числа. Второй студент теперь имеет лишь 9 возможностей (поскольку ему приходится заботиться о том, чтобы его число не совпало с задуманным числом первого студента N₂  N₁. Третий студент еще более ограничен в выборе — у него всего 8 возможностей (из 10 возможных для N₃ исключаются два числа: N₃  N₁ , N₃  N₂). Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, равно в силу той же основной теоремы m=10  9  8 = 720. Остальные случаи 1000 - 720 = 280 характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность совпадения равна Р=280/1000= 0,28.
Задача 3. Найти вероятность того, что в 8-значном числе ровно 4 цифры совпадают, а остальные различны.

Решение. Событие А={8-значное число содержит 4 одинаковые цифры}. Из условия задачи следует, что в числе 5 различных цифр, одна из них повторяется - число способов её выбора - любая из 10 цифр, и эта цифра занимает любые 4 места в числе – число способов . Оставшиеся 4 места занимают различные цифры из неиспользованных 9, и так как число зависит от порядка расположения цифр, то число способов выбора четырех цифр равно . Тогда число благоприятствующих исходов . Всего же способов составления 8-значных чисел равно ||=10⁸. Искомая вероятность равна .
Задача 4. Шесть клиентов случайным образом обращаются в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратится.

Решение. Рассмотрим обратное событие , состоящее в том, что в каждую из 5 фирм обратился клиент, тогда в какую-то из них обратились два человека, а в остальные 4 фирмы – по одному клиенту. Таких возможностей . А всего способов распределить 6 клиентов по 5 фирмам . Отсюда , следовательно .
Задача 5. Среди 25 экзаменационных билетов имеется 5 «счастливых» и 20 «несчастливых». Студенты подходят за билетами один за другим по очереди. У кого больше вероятность вытащить «счастливый» билет: у того, кто подошел первым, или у того, кто подошел вторым?

Решение. Пусть «счастливые» билеты имеют номера 1,2,3,4,5. Обозначим через i₁ номер билета, взятого первым студентом, через i₂ - номер билета, взятого вторым студентом, тогда элементарным исходом будет пара , а пространство элементарных исходов



здесь все элементарные исходы равновероятны. Событие А={первый студент взял «счастливый» билет} имеет вид



а событие В={второй студент взял «счастливый» билет} имеет вид:



Каждое из событий А и В содержит элементов, а все пространство  содержит элементов. Следовательно, Р(А)=Р(В)=1/5.
§ 3. Геометрическая вероятность.
Рассмотрим n-мерное вещественное пространство . Пусть в какую-то ограниченную область наудачу бросили точку. Слово «наудачу» означает, что в таком эксперименте все точки области «равновозможны». В этом случае вероятность попадания этой точки в какую-то подобласть определяется формулой



где и – n-мерные объемы областей и соответственно. Здесь элементарными исходами называются точки множества (которое играет роль пространства элементарных исходов), а благоприятствующими исходами – точки множества .
Задача 6. Точку наудачу бросили на отрезок . Какова вероятность попадания этой точки на интервал ?

Решение. Здесь пространство элементарных исходов весь отрезок , а множество благоприятствующих исходов , при этом длины этих интервалов равны и . Поэтому вероятность попадания брошенной точки в указанный интервал равна .
Задача 7. На отрезок бросили наудачу и поочередно две точки. Какова вероятность, что первая точка лежит правее второй точки?

Решение. Обозначим получившиеся координаты точек через x и y. Элементарным исходом в таком бросании двух точек будет пара , а пространством элементарных исходов – квадрат . Событие A={первая точка лежит правее второй точки} равносильно условию x>y, следовательно,

, т.е. представляет собой треугольник (см. рисунок). Площади квадрата и треугольника равны соответственно и , а потому вероятность .


Рис. 1.

Задачи для самостоятельного решения

1. 
   Построить пространство элементарных исходов для эксперимента, в котором монета бросается 3 раза.
   
2. 
   Построить пространство элементарных исходов для эксперимента, в котором вытаскиваются две карты из колоды в 36 карт.
   
3. 
   Четыре человека вошли в лифт на первом этаже шестиэтажного дома. Найти вероятности следующих событий: а) все пассажиры выйдут на шестом этаже; б) все пассажиры выйдут на одном и том же этаже; в) все пассажиры выйдут на разных этажах.
   
4. 
   Семь человек вошли в лифт на первом этаже восьмиэтажного дома. Какова вероятность, что на одном этаже вышли два человека?
   
5. 
   Бросают две игральные кости. Чему равна вероятность того, что сумма очков, выпавших на обеих костях, не превзойдет 5?
   
6. 
   Какова вероятность того, что в 4 бросаниях кости хотя бы один раз выпадет «единица»?
   
7. 
   Найти вероятность того, что дни рождения 12 человек приходятся на разные месяцы года.
   

8. 
   В урне 5 белых и 4 черных шара. Из урны наугад вынимают два шара. Какова вероятность того, что это будет: а) два белых шара; б) два черных шара; в) один черный и один белый.
   
9. 
   Пять клиентов случайным образом обращаются в 4 фирмы. Какова вероятность, что хотя бы в одну фирму никто не обратится?
   
10. 
    На остановке 10 человек случайным образом выбирают один из 10 вагонов поезда. Найти вероятность того, что ровно в один вагон никто не войдет.
    
11. 
    В каждой упаковке товара имеется одна из 5 различных наклеек. Какова вероятность собрать их все, купив 7 упаковок товара?
    
12. 
    Шесть шаров случайным образом раскладывают по 3 ящикам. Найти вероятность того, что во всех ящиках будет разное число шаров.
    
13. 
    Найти вероятность того, что в 6-значном номере 3 цифры совпадают , а остальные различны (считаем, что пятизначные номера могут начинаться с нуля).
    
14. 
    Семь человек становятся случайным образом в очередь один за другим. Какова вероятность того, что два определенных человека, скажем А и В, станут рядом?
    
15. 
    В очередь в булочную случайным образом встали 8 женщин и 2 мужчин. Какова вероятность того, что между мужчинами будут стоять 2 женщины.
    
16. 
    В очередь в кассу стоят 9 человек (трое мужчин, четыре женщины и двое детей). Какова вероятность, что между некоторыми двумя мужчинами будут стоять двое детей и одна женщина?
    
17. 
    В партии из 8 изделий 3 изделия – высшего качества. Найти вероятность того, что среди отобранных (без возвращения) 4 изделий – ровно одно изделие высшего качества.
    
18. 
    Из 10 проданных за день холодильников 4 имеют скрытые дефекты. Найти вероятность того, что среди выбранных наудачу 5 холодильников будет ровно 2 без скрытых дефектов.
    
19. 
    6 шаров случайным образом раскладываются по 3 ящикам. Найти вероятность того, что в первом ящике лежит 4 шара.
    
20. 
    На шахматную доску случайным образом поставлены две ладьи. Какова вероятность того, что они не будут бить друг друга?
    
21. 
    Группа из 18 студентов пишет контрольную работу из 3 вариантов (по 6 человек в каждом). Найти вероятность того, что среди случайно выбранных 5 студентов есть писавшие каждый вариант.
    
22. 
    На группу из 10 человек предоставлено для производственной практики 6 мест в лаборатории № 1 и 4 места – в лаборатории № 2. Какова вероятность того, что при случайном распределении мест двое неразлучных друзей из этой группы попадут на практику в одну лабораторию?
    
23. 
    В трех студенческих группах 72 человека (24 человека в группе по 12 юношей и 12 девушек). Наудачу выбраны 5 человек. Какова вероятность, что среди них будут девушки из всех трех групп?
    
24. 
    Из колоды в 36 карт выбираются наугад 4 карты. Найти вероятность, что среди них окажется хотя бы один туз.
    
25. 
    В лотерее из 50 билетов 5 выигрышных. Какова вероятность того, что среди первых пяти наугад выбранных билетов два будут выигрышными?
    
26. 
    Работа каждого из четырех студентов заочного отделения может проверяться одним из четырех преподавателей. Какова вероятность, что все четыре работы проверены разными преподавателями?
    
27. 
    Найти вероятность того, что в пятизначном числе имеются 2 четные цифры и 3 нечетные, при условии, что все они различны (считаем, что пятизначное число не может начинаться с нуля).
    
28. 
    В ящике находятся 5 белых, 3 красных и 2 черных шара. Наудачу выбирает 6 шаров. Найти вероятность того, что выборка будет содержать 3 белых, 2 красных и 1 черный шар, если: а) выборка производится без возвращения (все 6 шаров отбираются сразу); б) выборка производится с возвращением (фиксируется цвет выбранного шара, после чего он возвращается в ящик).
    
29. 
    Какова вероятность, что дуэль состоится, если каждый из дуэлянтов приходит на место дуэли в случайный момент времени между 5 и 6 часами и ждет противника в течение 5 минут?
    
30. 
    Две подруги договорились встретиться в условленном месте в промежутке от 17 до 19 часов. Пришедшая первой ждет другую не более 15 минут. Какова вероятность, что подруги не встретятся?
    
31. 
    На отрезок [2,5] наудачу бросаются две точки. Какова вероятность, что расстояние между ними меньше 2?
    
32. 
    На отрезок [-1,2] наудачу брошены две точки. Какова вероятность, что расстояние между ними больше 1?
    
33. 
    Точку бросают случайным образом на квадрат площади 100см². Какова вероятность, что координаты x,y этой точки отличаются друг от друга не более, чем на 1 см?
    
34. 
    Два теплохода должны подойти к одному и тому же причалу. Время прихода обоих теплоходов независимо и равновозможно в течение данных суток. Найти вероятность того, что ни одному из теплоходов не придется ожидать освобождения причала, если время стоянки первого теплохода — 1 час, а второго — 2 часа.
    
35. 
    Студент может добраться до факультета либо на автобусе, интервал движения которого составляет 7 минут, либо на троллейбусе, интервал движения которого составляет 10 минут. Найти вероятность того, что студенту, пришедшему на остановку в случайный момент времени, придется ждать не более трех минут.
    
36. 
    Наудачу взяты два положительных числа Х и Y, каждое из которых не превышает единицы. Найти вероятность того, что сумма Х + Y не превышает 1, а произведение ХY не меньше 0,09.
    
37. 
    Найти вероятность того, что из трех наудачу взятых отрезков длиной не более L можно построить треугольник.
    
38. 
    В точке С, положение которой на телефонной линии АВ длиной 10 км равно возможное, произошел разрыв. Определить вероятность того, что точка С удалена от точки А, где находится ремонтная станция, на расстояние, не меньшее 1 км.
    
39. 
    На плоскость с нанесенной сеткой квадратов со стороной а брошена монета радиуса . Найти вероятность того, что монета не пересечет ни одной из сторон квадрата.
    
40. 
    Найти вероятность максимального выигрыша в спортлото (угадать 6 из 49).
    
41. 
    В пачке 1000 лотерейных билетов, из которых 10 выигрышные. Какова вероятность выиграть хоть что-нибудь, имея: а) 3 билета; б) 100 билетов?
    
42. 
    Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 2а. На плоскость бросают наудачу иглу длиной 2l (l  а). Найти вероятность того, что игла пересечет какую-нибудь прямую.