Нелинейное программирование. Классическая задача
 Скачать 174.34 Kb. Скачать 174.34 Kb.
|
|
Нелинейное программирование. Классическая задачаЗадача линейного программирования, в которой целевая функция и (или) ограничения являются нелинейной функцией называется задачей нелинейного программирования (степенные, трансцендентные). Рассмотрим классическую задачу , которая была сформулирована и решена Лагранжем в 1798 году.  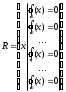 Лагранж с помощью специальной функции свел эту задачу к задаче на безусловный экстремум, используя при этом теорему Ферма.  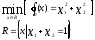 (2) (2)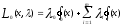 (3) (3)Чтобы можно было применять функцию Лагранжа , необходимо : 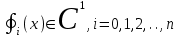 принадлежали классу непрерывных дифференцируемых функций. принадлежали классу непрерывных дифференцируемых функций.Задача (1)-(2) имеет решение если существует вектор 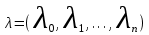 , причем , причем 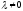 ; называется множителем Лагранжа и для которого выполняются условия: ; называется множителем Лагранжа и для которого выполняются условия: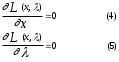 (необходимое условие экстремума) (необходимое условие экстремума)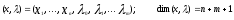 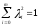 (6) (6)Если априори известно, что задача (1)-(2) - имеет решение , то множитель 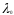 полагается равным 1. полагается равным 1.Решим наш пример с помощью формализма Лагранжа 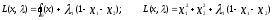 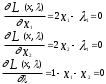 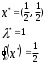 Достаточное условие экстремума: для определения точки экстремума , получаемой из условия (4), (5), необходимо провести дополнительные исследования, т. Е. Использовать достаточные условия , которые заключаются в следующем: рассматривается матрица вторых производных - так называемый гессиан или матрица Гесса: 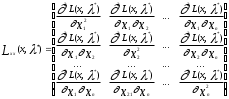 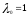 , которая позволит нам определить какую точку экстремума мы нашли. , которая позволит нам определить какую точку экстремума мы нашли.Если матрица Гессе положительно определена в точке х*, то точка х* является точкой минимума ,а если отрицательно определена - то точкой максимума. Матрица называется положительно определенной , если все ее собственные числа 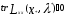 (7) (7)Матрица называется отрицательно определенной если все ее собственные числа 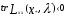 (8) (8)Если же матрица имеет собственные числа как положительные так и отрицательные, то о ее определенности ничего сказать нельзя. Если в неравенствах (7) и (8) имеет место знак нестрогих неравенств, то они называются положительно полуопределенными и отрицательно полуопределенными. Кроме неравенств (7) и (8), матрицы требуют дополнительных исследований для установления вида экстремума. Для определения вида экстремума используется так называемый критерий Сильвестра. Теорема: матрица 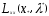 является положительно определенной тогда и только тогда, когда все ее главные миноры положительны является положительно определенной тогда и только тогда, когда все ее главные миноры положительны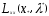 = = Минор первого порядка 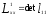 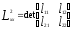 ... ... ... 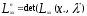 Матрица 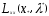 будет отрицательно определена, если все ее главные миноры удовлетворяют следующему неравенству будет отрицательно определена, если все ее главные миноры удовлетворяют следующему неравенству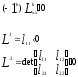 Главные миноры должны быть знакочередующимися, причем первый минор должен быть отрицательным. 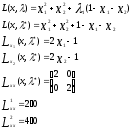 это точка минимума Пример : Исследовать условный экстремум функции f0(x) в области 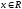 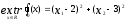 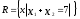 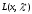 = =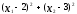 - -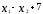 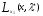 =2 =2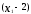 -2=0 -2=0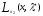 =2 =2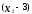 -2=0 -2=0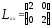 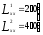 точка минимума точка минимума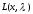 = =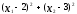 - -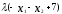 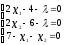 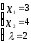 Ответ: 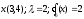 точка экстремума точка экстремумаГеометрическая интерпретация с помощью линий уровня. Линии уровня это сечение плоскостями параллельными координатной плоскости Х1ОХ2 . Получаем систему концентрических окружностей 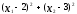 =R2 =R2 Общая задача нелинейного программирования. Постановка задачи. 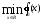 (1) (1)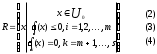 - ограничение типа включения, U0 - простейший случай и может иметь следующий вид 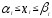 это параллелепипед . это параллелепипед .Обобщенное правило Лагранжа Если функции f0,f1,...,fm - дифференцируемы ;fm+1.,fm+2, ..., fs - непрерывно дифференцируемы в окрестности точки х* ,то существуют множители Лагранжа 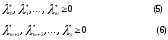 , такие . что выполняются условия , такие . что выполняются условия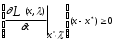  (7) (7)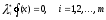 (8) (8)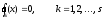 (9) (9)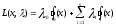 (10) (10)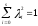 (11) (11)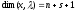 - условие дополняющей нежесткости 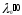 ,т.к. задача решается на минимум, а ,т.к. задача решается на минимум, а 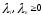 , т.к. (3)-ограничение типа неравенств , т.к. (3)-ограничение типа неравенств-соответствует 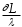 б это ограничение условия связи. б это ограничение условия связи.При оптимальном решение  часть ограничений (8) выполняются как строгие неравенства и соответствующие им множители Лагранжа не равны 0, а часть ограничений (8) выполняется как строгое равенство. На этом свойстве основано решение общей задачи нелинейного программирования. часть ограничений (8) выполняются как строгие неравенства и соответствующие им множители Лагранжа не равны 0, а часть ограничений (8) выполняется как строгое равенство. На этом свойстве основано решение общей задачи нелинейного программирования.Общая задача решается так: Сначала решается задача (1) при ограничениях (4) , т.е. классическая задача. Полученное решение подставляют в (2)и (3) и те из ограничений неравенств, которые не выполняются, добавляются как равенства к условию (4) и полученная классическая задача решается снова. И так, пока не выполним все условия (2) И (3). Замечание1: множители Лагранжа позволяют свести исходную задачу на условный экстремум (нахождение экстремума целевой функции при наличие ограничений) к задаче на безусловный экстремум нахождения минимальной функции Лагранжа (10). Используя необходимые условия экстремума для функции Лагранжа , переходим к решению системы уравнений и получаем решение  . Или можно найти экстремум функции Лагранжа, используя численные методы: градиентный. . Или можно найти экстремум функции Лагранжа, используя численные методы: градиентный.Замечание 2:найденные точки , удовлетворяющие необходимому условию экстремума должны обязательно проверяться на их свойства с помощью критерия Сильвестра. Интерпретация множителей Лагранжа.  (1) (1)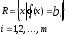 (2) (2)Пусть эта задача имеет оптимальное решение 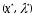 и исследуем зависимость решения от вектора правой части и исследуем зависимость решения от вектора правой части 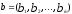 , , 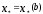 Исследуем зависимость целевой функции (10) 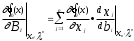 (3) (3)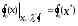 Исследуем зависимость ограничений (2) 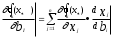 (4) (4)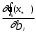 = =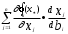 = =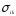 (4/) (4/)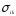 - символ Кронекера - символ Кронекера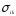 = =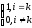 0= 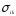 - -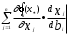 (5) (5)умножаем на соответствующие 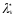 и прибавляем к (3) и прибавляем к (3)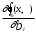 = =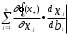 - -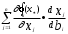 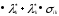 (6) (6)просуммируем (6) по k : 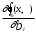 = =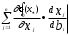 - -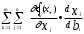 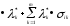 Объединим суммы 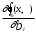 = =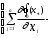 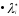 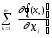  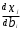 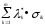 (7) (7)В (7) принимаем 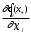 =0; =0; 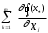 =0 как необходимое условие экстремума. =0 как необходимое условие экстремума. = =  = = (8) (8)Множители Лагранжа показывает зависимость целевой функции от значения вектора свободных членов. И если задача (1),(2) есть задача распределения ресурсов, то множители Лагранжа показывает эффективность использования того или иного ресурса. Это экономическая интерпретация множителей Лагранжа. |
