самостоятельная работа. ср по моис. Классификация и кластеризация
 Скачать 345.62 Kb. Скачать 345.62 Kb.
|
|
Факультет СФИТ ТУИТ-БГУИР Направление Искусственный интеллект Самостоятельная работа По предмету МОИС На тему: Классификация и кластеризация Классификация - системное распределение изучаемых предметов, явлений, процессов по родам, видам, типам, по каким-либо существенным признакам для удобства их исследования; группировка исходных понятий и расположение их в определенном порядке, отражающем степень этого сходства. Классификация является наиболее простой и одновременно наиболее часто решаемой задачей Data Mining. Классификация требует соблюдения следующих правил: в каждом акте деления необходимо применять только одно основание; деление должно быть соразмерным, т. е. общий объем видовых понятий должен равняться объему делимого родового понятия; члены деления должны взаимно исключать друг друга, их объемы не должны перекрещиваться; деление должно быть последовательным. Различают классификации: вспомогательную (искусственную) классификацию - производится по внешнему признаку и служит для придания множеству предметов (процессов, явлений) нужного порядка; естественную классификацию - производится по существенным признакам, характеризующим внутреннюю общность предметов и явлений. Она является результатом и важным средством научного исследования, т. к. предполагает и закрепляет результаты изучения закономерностей классифицируемых объектов. В зависимости от выбранных признаков, их сочетания и процедуры деления понятий классификация может быть: простой - деление родового понятия только по признаку и только один раз до раскрытия всех видов. Примером такой классификации является дихотомия, при которой членами деления бывают только два понятия, каждое из которых является противоречащим другому (т. е. соблюдается принцип: "А и не А"); сложной - применяется для деления одного понятия по разным основаниям и синтеза таких простых делений в единое целое. Пример - периодическая система химических элементов. Под классификацией понимают отнесение объектов (наблюдений, событий) к одному из заранее известных классов. Классификация - это закономерность, позволяющая делать вывод относительно определения характеристик конкретной группы. Таким образом, для проведения классификации должны присутствовать признаки, характеризующие группу, к которой принадлежит то или иное событие или объект (обычно при этом на основании анализа уже классифицированных событий формулируются некие правила). Классификация относится к стратегии обучения с учителем ( supervised learning), которое также именуют контролируемым или управляемым обучением. Задачей классификации часто называют предсказание категориальной зависимой переменной (т. е. зависимой переменной, являющейся категорией) на основе выборки непрерывных и/или категориальных переменных. Например, можно предсказать, кто из клиентов фирмы является потенциальным покупателем определенного товара, а кто - нет, кто воспользуется услугой фирмы, а кто - нет, и т. д. Этот тип задач относится к задачам бинарной классификации, в них зависимая переменная может принимать только два значения (например, да или нет, 0 или 1). Другой вариант классификации возникает, если зависимая переменная может принимать значения из некоторого множества предопределенных классов. Например, когда необходимо предсказать, какую марку автомобиля захочет купить клиент. В этих случаях рассматривается множество классов для зависимой переменной. Классификация может быть одномерной (по одному признаку) и многомерной (по двум и более признакам). Многомерная классификация - разработана биологами при решении проблем дискриминации для классифицирования организмов. В работе Р. Фишера ( 1930г.) организмы разделялись на подвиды в зависимости от результатов измерений их физических параметров. Биология - востребованная и удобная среда для разработки многомерных методов классификации. Пример задачи классификации. Пусть имеется БД о клиентах туристического агентства с информацией о возрасте и доходе за месяц. Есть рекламный материал двух видов: более дорогой и более дешевый отдых. Определены два класса клиентов: класс 1 и 2.
Процесс классификации Цель процесса классификации - построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута. Процесс классификации - в разбиении множества объектов на классы по определенному критерию. Классификатором называется сущность, определяющая, какому из предопределенных классов принадлежит объект по вектору признаков. Для проведения классификации с помощью математических методов необходимо иметь формальное описание объекта, которым можно оперировать, используя математический аппарат классификации. Таким описанием в примере выступает БД. Каждый объект ( запись БД ) несет информацию о некотором свойстве объекта. Набор исходных данных (выборку) разбивают на два множества: обучающее и тестовое. Обучающее множество ( training set) - множество, которое включает данные, использующиеся для обучения (конструирования) модели. Такое множество содержит входные и выходные (целевые) значения примеров. Выходные значения предназначены для обучения модели. Тестовое (test set) множество также содержит входные и выходные значения примеров. Здесь выходные значения используются для проверки работоспособности модели. Процесс классификации состоит из двух этапов: конструирования модели и ее использования. Этап 1. Конструирование модели: описание множества предопределенных классов. Каждый пример набора данных относится к одному предопределенному классу. Используется обучающее множество, на нем происходит конструирование модели. Полученная модель может быть представлена классификационными правилами, деревом решений или математической формулой. Этап 2. Использование модели: классификация новых или неизвестных значений. Оценка правильности (точности) модели. 2.1. Известные значения из тестового примера сравниваются с результатами использования полученной модели. 2.2. Уровень точности - процент правильно классифицированных примеров в тестовом множестве. 2.3. Тестовое множество, т. е. множество, на котором тестируется построенная модель, не должно зависеть от обучающего множества. Если точность модели допустима, возможно использование модели для классификации новых примеров, класс которых неизвестен. Методы, применяемые для решения задач классификации Для классификации используются различные методы. Основными из них являются: классификация с помощью деревьев решений; байесовская (наивная) классификация; классификация при помощи искусственных нейронных сетей; классификация методом опорных векторов; статистические методы, в частности, линейная регрессия; классификация при помощи метода ближайшего соседа; классификация CBR-методом; классификация при помощи генетических алгоритмов. Схематическое решение задачи классификации некоторыми методами (при помощи линейной регрессии, деревьев решений и нейронных сетей) приведены на рисунках. (а-в) 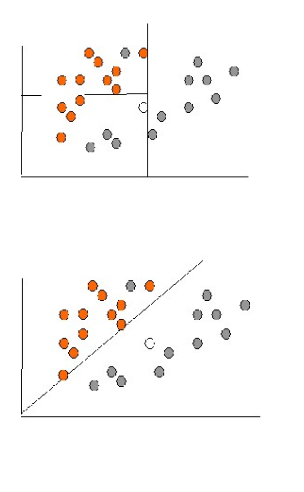 (а)- метод линейной регрессии (а)- метод линейной регрессии(б) - метод деревьев решений 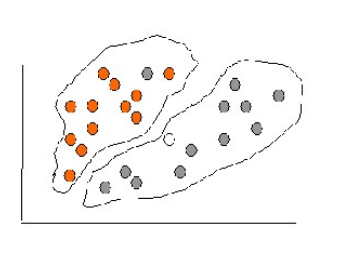 (в) – метод нейронных сетей (в) – метод нейронных сетей Точность классификации: оценка уровня ошибок Оценка точности классификации может проводиться при помощи кросс-проверки. Кросс-проверка (Cross-validation) - это процедура оценки точности классификации на данных из тестового множества, которое также называют кросс-проверочным множеством. Точность классификации тестового множества сравнивается с точностью классификации обучающего множества. Если классификация тестового множества дает приблизительно такие же результаты по точности, как и классификация обучающего множества, считается, что данная модель прошла кросс-проверку. Разделение на обучающее и тестовое множества осуществляется путем деления выборки в определенной пропорции, например обучающее множество - две трети данных и тестовое - одна треть данных. Этот способ следует использовать для выборок с большим количеством примеров. Если же выборка имеет малые объемы, рекомендуется применять специальные методы, при использовании которых обучающая и тестовая выборки могут частично пересекаться. Оценивание классификационных методов Оценивание методов следует проводить, исходя из следующих характеристик: скорость, робастность, интерпретируемость, надежность. Скорость характеризует время, которое требуется на создание модели и ее использование. Робастность, т. е. устойчивость к каким-либо нарушениям исходных предпосылок, означает возможность работы с зашумленными данными и пропущенными значениями в данных. Интерпретируемость обеспечивает возможность понимания модели аналитиком. Свойства классификационных правил: размер дерева решений; компактность классификационных правил. Надежность методов классификации предусматривает возможность работы этих методов при наличии в наборе данных шумов и выбросов. Задача кластеризации Задача кластеризации сходна с задачей классификации, является ее логическим продолжением, но ее отличие в том, что классы изучаемого набора данных заранее не предопределены. Синонимы термина "кластеризация": "автоматическая классификация", "обучение без учителя" и " таксономия". Кластеризация предназначена для разбиения совокупности объектов на однородные группы ( кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек". Цель кластеризации - поиск существующих структур. Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных". Само понятие "кластер" определено неоднозначно: в каждом исследовании свои "кластеры". Переводится понятие кластер (cluster) как "скопление", "гроздь". Кластер можно охарактеризовать как группу объектов, имеющих общие свойства. Характеристиками кластера можно назвать два признака: внутренняя однородность; внешняя изолированность. Вопрос, задаваемый аналитиками при решении многих задач, состоит в том, как организовать данные в наглядные структуры, т.е. развернуть таксономии. Наибольшее применение кластеризация первоначально получила в таких науках как биология, антропология, психология. Для решения экономических задач кластеризация длительное время мало использовалась из-за специфики экономических данных и явлений. В таблице приведено сравнение некоторых параметров задач классификации и кластеризации. На рисунке схематически представлены задачи классификации и кластеризации.
 Сравнение задач классификации и кластеризации Кластеры могут быть непересекающимися, или эксклюзивными (non- overlapping, exclusive), и пересекающимися (overlapping). 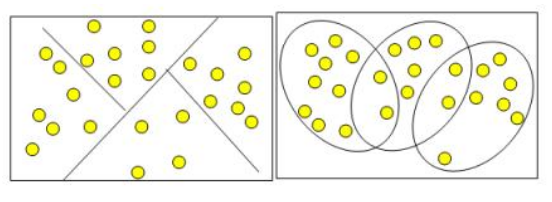 Непересекающиеся и пересекающиеся кластеры. В результате применения различных методов кластерного анализа могут быть получены кластеры различной формы. Например, возможны кластеры "цепочного" типа, когда кластеры представлены длинными "цепочками", кластеры удлиненной формы и т. д., а некоторые методы могут создавать кластеры произвольной формы. Различные методы могут стремиться создавать кластеры определенных размеров (например, малых или крупных) либо предполагать в наборе данных наличие кластеров различного размера. Некоторые методы кластерного анализа особенно чувствительны к шумам или выбросам, другие - менее. В результате применения различных методов кластеризации могут быть получены неодинаковые результаты, это нормально и является особенностью работы того или иного алгоритма. Данные особенности следует учитывать при выборе метода кластеризации. На сегодняшний день разработано более сотни различных алгоритмов кластеризации. Краткая характеристика подходов к кластеризации. Алгоритмы, основанные на разделении данных (Partitioning algorithms): разделение объектов на k кластеров; итеративное перераспределение объектов для улучшения кластеризации. Иерархические алгоритмы ( Hierarchy algorithms): агломерация: каждый объект первоначально является кластером, кластеры, соединяясь друг с другом, формируют больший кластер и т. д. Методы, основанные на концентрации объектов ( Density-based methods): основаны на возможности соединения объектов; игнорируют шумы, нахождение кластеров произвольной формы. Грид-методы (Grid-based methods): квантование объектов в грид-структуры. Модельные методы (Model-based): использование модели для нахождения кластеров, наиболее соответствующих данным. Применение кластерного анализа Кластерный анализ применяется в различных областях. Он полезен, когда нужно классифицировать большое количество информации. В медицине используется кластеризация заболеваний, лечения заболеваний, их симптомов, таксономия пациентов, препаратов и т. д. В археологии устанавливаются таксономии каменных сооружений и древних объектов и т.д. В маркетинге это задача сегментации конкурентов и потребителей. В менеджменте - разбиение персонала на различные группы, классификация потребителей и поставщиков и др. В медицине - классификация симптомов. В социологии - разбиение респондентов на однородные группы. Кластерный анализ в маркетинговых исследованиях применяется достаточно широко - как в теоретических исследованиях, так и практикующими маркетологами, решающими проблемы группировки различных объектов. Решаются вопросы о группах клиентов, продуктов и т.д. Важная задача - анализ поведения потребителя: группировка потребителей в однородные классы для получения максимально полного представления о поведении клиента из каждой группы и о факторах, влияющих на его поведение. Другая важная задача - позиционирование - определение ниши, в которой следует позиционировать новый продукт, предлагаемый на рынке. В результате применения кластерного анализа строится карта, по которой можно определить уровень конкуренции в различных сегментах рынка и соответствующие характеристики товара для возможности попадания в этот сегмент. С помощью анализа такой карты возможно определение новых, незанятых ниш на рынке, в которых можно предлагать существующие товары или разрабатывать новые. Кластерный анализ удобен и для анализа клиентов компании. Все клиенты группируются в кластеры, и для каждого кластера вырабатывается индивидуальная политика. Такой подход позволяет сократить объекты анализа, и индивидуально подойти к каждой группе клиентов. Практика применения кластерного анализа в маркетинговых исследованиях. Несмотря на кажущуюся похожесть задачи классификации и кластеризации решаются разными способами и при помощи разных методов. Различие задач - в исходных данных. Классификация - наиболее простая задача Data Mining, относится к стратегии "обучение с учителем", для ее решения обучающая выборка должна содержать значения входных и выходных (целевых) переменных. Кластеризация, напротив, является задачей Data Mining, относящейся к стратегии "обучение без учителя", т. е. не требует наличия значения целевых переменных в обучающей выборке. Задача классификации решается при помощи различных методов, наиболее простой - линейная регрессия. Выбор метода должен базироваться на исследовании исходного набора данных. Распространенные методы решения задачи кластеризации: метод k-средних (работает только с числовыми атрибутами), иерархический кластерный анализ (работает также с символьными атрибутами), метод SOM. Сложностью кластеризации является необходимость ее оценки. |
