|
|
Расчет защит. Классификация источников излучения
4.1.2.2 Расчет поля γ- излучения с учетом многократного рассеяния в материале защиты
Так же как и в случае точечных источников, многократное рассеяние излучения протяженных источников существенным образом влияет на величину общего ослабления излучения в защите, а, следовательно, на мощность дозы за защитой. Основная трудность при теоретическом рассмотрении ослабления γ- излучения протяженных источников с учетом многократного рассеяния в защите связана с тем, что фактор накопления рассеянного излучения сложным образом зависит от величины µх, атомного номера материала защиты Z и энергии γ- излучения Е.
Используются два способа расчета поля γ- излучения за защитой от протяженных источников.
Первый способ с помощью аналитического представления факторов накопления - формула (4.1.1.5). Для описания этого метода воспользуемся источником в виде усеченного конуса «бесконечной» (µsh>3) высоты.
Мощность экспозиционной дозы нерассеянного излучения за слоем защиты толщиной x:
 (4.1.2.2.1) (4.1.2.2.1)
где µs – линейный коэффициент ослабления γ- квантов в материале источника;
Г – гамма-постоянная радионуклида, Р*см /(ч*мКи);
qv – удельная мощность источника, МэВ/(см *с).
В этом методе фактор накопления в форме (4.1.1.5) подставляют в подинтегральное выражение функции ослабления протяженных источников и интегрируют с новым показателем экспоненты. Это не усложняет процедуры интегрирования, поскольку вид начальной функции не изменяется. Если обозначить g(µx) функцию, характеризующую поле нерассеянного и рассеянного излучения, то функция ослабления имеет вид
G=A1G(µꞌx)+(1–A1)G(µꞌꞌx),
где µꞌ= (1+α1) µ;
µꞌꞌ= (1+α2) µ.
Применительно к выбранному здесь примеру вместо соотношения
получается выражение для Рэкс от γ- излучения источника в форме усеченного конуса
 . (4.1.2.2.3) . (4.1.2.2.3)
Собственно фактор накопления протяженного источника В может быть определен по этому способу так
B=[A1G( )+(1–A1)G( )+(1–A1)G( )]/G(µx). (4.1.2.2.4) )]/G(µx). (4.1.2.2.4)
Второй способ с помощью эквивалентной толщины ослабления. Обозначим G(0)и G(µx) функции, характеризующие поле нерассеянного излучения протяженного источника без защитного экрана толщиной µx.Если бы источник был точечный, то кратность ослабления k(µx)нерассеянного излучения можно было бы записать в форме
k(µx)=exp(µx). (4.1.2.2.5)
Для протяженного источника авторы данного метода Д.П.Осанов и Е.Е.Ковалев предложили вместо (4.1.2.2.5) выражение
k(µx)=exp(µl), (4.1.2.2.6)
где µl– эквивалентная толщина защиты, которая определяется из соотношения
µl=ln[G(0)/G(µx)]=lnk(µx). (4.1.2.2.7)
Тогда фактор накопления протяженного источника B(E0,µl,Z) количественно можно определить, используя для этого табличные данные фактора накопления точечного источника, но с входным параметром µ1,определяемым соотношением (4.1.2.2.7). Поскольку µl µx (а фактор накопления возрастает с толщиной), B(E0,µl,Z)>B(E0,µl,Z).Преимущество этого способа учета многократного рассеяния перед предыдущим состоит в том, что здесь отпадает необходимость вводить факторы накопления в подинтегральное выражение функций ослабления. Так же, как для точечного источника, многократное рассеяние в защите учитывается умножением функции ослабления на B(E0,µl,Z). Вместо выражения (4.1.2.2.1) можно написать µx (а фактор накопления возрастает с толщиной), B(E0,µl,Z)>B(E0,µl,Z).Преимущество этого способа учета многократного рассеяния перед предыдущим состоит в том, что здесь отпадает необходимость вводить факторы накопления в подинтегральное выражение функций ослабления. Так же, как для точечного источника, многократное рассеяние в защите учитывается умножением функции ослабления на B(E0,µl,Z). Вместо выражения (4.1.2.2.1) можно написать
 (4.1.2.2.8) (4.1.2.2.8)
где фактор накопления определяется по эквивалентной длине ослабления
 . (4.1.2.2.9) . (4.1.2.2.9)
Используя фактор накопления протяженных источников, следует учитывать степень точности, которая необходима при проектировании защиты. Как показывает анализ, эффект протяженности источника в худшем случае (на близких расстояниях) увеличивает фактор накопления в 1,35 раза. Для наиболее часто используемых условий проектирования это различие лежит в пределах 1,05-1,07. Поэтому при оценочных расчетах не всегда целесообразно вводить поправку на протяженность источника. Кроме того, необходимо иметь в виду, что литературные данные о численных значениях факторов накопления обычно относятся к бесконечной среде и, следовательно, включают эффект обратного рассеяния. Эффект барьерности для легких сред уменьшает фактор накопления в 1,2-1,3 раза по сравнению с бесконечной геометрией. Таким образом, эти два эффекта в значительной степени компенсируют друг друга. Поэтому можно считать оправданной распространенную практику применения факторов накопления точечных источников в бесконечной среде в расчетах барьерной защиты из легких сред для протяженных источников.
Метод определения факторов накопления для протяженных источников с помощью приближенного аналитического выражения фактора накопления для точечного источника позволяет учитывать рассеяние излучения в защите от элементарных источников, образующих тот или иной протяженный источник. Практическое использование этого метода для учета рассеяния монохроматического излучения обеспечивает достаточную точность, но несколько затрудняется необходимостью предварительного определения ряда числовых коэффициентов и функций ослабления G(µ'x) и G(µ"x).Для источников со сложным спектром излучения рассмотренный выше метод становится громоздким.
Определение факторов накопления для протяженных источников можно существенно упростить, если находить их в интегральной форме сразу для всего объема или поверхности протяженного объема [2], [7].
4.1.2.3 Защита от γ- излучения линейных и поверхностных источников
Линейные и поверхностные источники отличаются от других протяженных источников тем, что самопоглощение и саморассеяние излучения в этом случае практически пренебрежимо мало. Это обстоятельство существенно упрощает расчеты защиты, поскольку для таких источников спектр излучения, падающего на защиту, однозначно определяется изотопным составом радиоактивного вещества, распределенного по поверхности источника. В связи с этим для решения задачи о величине дозы излучения, создаваемой линейным или поверхностным источником за защитным экраном, достаточно знать функцию излучения для данной геометрии источника и метод учета многократного рассеяния излучения в защите.
Для всех протяженных источников характерен более быстрый спад мощности дозы излучения при возрастании толщины защитного экрана по сравнению с точечным источником [7].
4.1.2.4 Защита от γ- излучения объемных источников
Графический метод расчета. В этом методе используется система номограмм [2]. Рассмотрим графический метод расчета защиты от цилиндрического источника. Для определения по номограмме требуемой толщины защиты µx без учета рассеянного излучения необходимо знать: фиктивный удельный гамма-эквивалент, мг-экв Rа*см/л,
Mф = αMv/ µs,
Где α – коэффициент, учитывающий отклонение от стандартных условий проектирования защиты;
Mv – удельный гамма-эквивалент источника, мг-экв Ra/л;
µs – линейный коэффициент ослабления γ- излучения в материале источника.
Система номограмм дает возможность найти толщину защиты без учета многократного рассеяния. Для определения толщины защиты х0 с учетом многократного рассеяния γ- излучения в материале защиты используется формула вида
 (4.1.2.4.2) (4.1.2.4.2)
где µ – линейный коэффициент ослабления γ- излучения в материале
защиты;
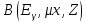 – фактор накопления γ-излучения в бесконечной среде для точечного источника с энергией Еγ в защите толщиной µх с атомным номером материала Z [1]. – фактор накопления γ-излучения в бесконечной среде для точечного источника с энергией Еγ в защите толщиной µх с атомным номером материала Z [1].
Расчет по заданной кратности ослабления. При проектировании защиты от γ- излучения объемных источников в качестве исходного параметра иногда берут кратность ослабления. Это делают чаще всего, когда известны лишь измеренные уровни излучения и когда необходимо учесть экранирующий эффект окружающих источник конструкций (например, в системе активной зоны и теплоносителя атомного реактора), а также при расчете гетерогенной защиты. Принцип построения универсальных таблиц может быть применен и для протяженных источников. Для цилиндрического источника в радиальном направлении зависимость кратности ослабления нерассеянного излучения k(µx)от толщины защиты µx может быть получена из соотношения
k (µx) = [G(k, p, µs, R, µx=0)]/[G(k, p, µs,R, µx)], (4.1.2.4.3)
где k = h/R – относительная высота цилиндрического источника;
p= b/R– относительное расстояние от оси цилиндра до точки наблюдения;
b – расстояние от оси цилиндра до точки наблюдения;
h и R – высота и радиус цилиндра;
µ – линейный коэффициент ослабления γ- излучения в материале защиты;
G– функция ослабления в защите излучения цилиндрического источника.
Как и для точечного источника, для протяженных источников можно построить кривые зависимости кратности ослабления от абсолютной толщины с учетом многократного рассеяния в защите. Тогда вместо формулы (4.1.2.4.3) используется формула
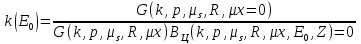 , (4.1.2.4.4) , (4.1.2.4.4)
где ВЦ - фактор накопления цилиндрического источника.
Расчет защиты для немоноэнергетических источников γ- излучения. При наличии сложного спектра в расчетах защиты используют метод конкурирующих линий или интегральный метод.
Метод конкурирующих линий. При сложном немоноэнергетическом спектре излучения источника его разбивают на несколько энергетических интервалов и определяют для них эффективную энергию E01, Е02, …, Е0т и соответствующий вклад п1, п2, ..., пт (%) каждой энергии. Удобно располагать E0i в порядке уменьшения энергии, т.е. E01>E02>...>E0m, и, следовательно (если Е01 меньше критической энергии), в порядке уменьшения проникающей способности. Необходимо избегать разделения спектра на большое количество энергетических интервалов и вместе с тем не объединять в один интервал энергии с существенно различным сечением взаимодействия. В практике расчета защиты (например, от γ- излучения смеси продуктов деления или γ - излучения активной зоны реактора) ограничиваются обычно тремя - пятью энергетическими интервалами. Затем для каждой эффективной энергии (с учетом ее относительного вклада в мощность дозы или интенсивность) с помощью рассмотренных выше или иных методов определяют необходимую толщину защиты. Таким образом, получают набор значений толщиныx1, х2, x3, ..., хт.
Главной линией спектра условно называется та, для которой требуется наибольшая толщина защиты (хгл). Линия спектра, которая требует меньшей толщины защиты (хк), называется конкурирующей. Толщина защиты х, которая должна быть принята, с хорошим приближением может быть определена из соотношений
если (xгл – xк) = 0, то x = xгл+ Δ1/2;
если (xгл – xк) < Δ1/2, то x = xк+ Δ1/2; (4.1.2.4.5)
если (xгл – xк) > Δ1/2, то x = xгл.
где Δ1/2 – слой половинного ослабления.
В связи с тем что Δ1/2 зависит от кратности ослабления (и, следовательно, от толщины защиты) хгл и хк. Разница в толщинах между выбранными и удвоенными значениями кратностей ослабления или удельных активностей и есть слой половинного ослабления. При этом выбирают ту энергию, которая дает наибольшее значение Δ1/2: она может соответствовать и главной и конкурирующей линии, потому что по мере увеличения абсолютной толщины защиты главная и конкурирующая линии могут меняться местами или даже уступать место третьей линии, которая раньше была второстепенной. Этот метод и формулы (4.1.2.4.5) применяют при решении задач защиты и от других видов ионизирующих излучений, например от нейтронов.
Интегральный метод расчета защиты. Если спектр γ- излучения постоянен, целесообразно использовать интегральный метод расчета защиты. Наиболее удобно и универсально в этом случае построение номограмм по формуле (4.1.2.1.2), т.е. построение зависимостей интегральных кратностей ослабления от толщины защиты. Формулу (4.1.2.1.2) можно записать в виде
 (4.1.2.4.6) (4.1.2.4.6)
Отсюда эффективный коэффициент ослабления для первичного и рассеянного γ - излучения источника сложного спектра равен
 (4.1.2.4.7) (4.1.2.4.7)
Здесь обозначения те же, что и в формуле (4.1.2.1.2). Если первичное излучение моноэнергетическое, то
µЭФ (x) = (µx– lnB)/x,
где µ – коэффициент ослабления γ- излучения в геометрии узкого пучка.
Таким образом, при интегральном методе защита рассчитывается с использованием обычных функций ослабления излучения, но вместо коэффициента ослабления в геометрии узкого пучка µ берут эффективный коэффициент ослабления µЭФ, рассчитанный в геометрии широкого пучка. Как видно из уравнения (4.1.2.4.8), µЭФ зависит от толщины защиты даже при моноэнергетическом спектре первичного излучения. В случае сложного спектра эта зависимость еще сильней [2].
4.1.2.5 Ослабление γ- излучения цилиндрических источников в защите
Защита от излучения в радиальном направлении. Оценка ослабления излучения, выходящего из цилиндрического источника в радиальном направлении, основанная на точном учете его реальной формы, может быть произведена следующим образом.
Мощность дозы в точке A1 за плоской защитой (рисунок 4.1.2.5.1), определяется выражением
P = 2PγqRG1( k, p, µ0, R, µd ), (4.1.2.5.1)
где k = h/R– относительная высота цилиндрического источника;
р –b/R - относительное расстояние от точки А1 до оси цилиндра;
Рγ – γ-постоянная изотопа;
q – удельная активность объемного источника;
G1( k, p, µ0, R, µd ), – функция ослабления в защите излучения цилиндрических источников.
Эти же данные могут быть применены и для определения мощности дозы в любой другой точке, лежащей в пределах высоты цилиндра, в радиальном направлении. В частности, для точки в плоскости центрального сечения А2 того же цилиндра
P=4PγqRG1(k',p,µ0,R,µd), (4.1.2.5.2)
где k'=k/2R.
Защита от излучения в направлении оси. Обычно при рассмотрении излучения за защитой в этом направлении цилиндр заменяется усеченным конусом. Рассмотрим непоглощающий цилиндрический источник. Мощность дозы в точке А3, находящейся на оси цилиндра, определяется выражением
Р = Р'+Р". (4.1.2.5.3).
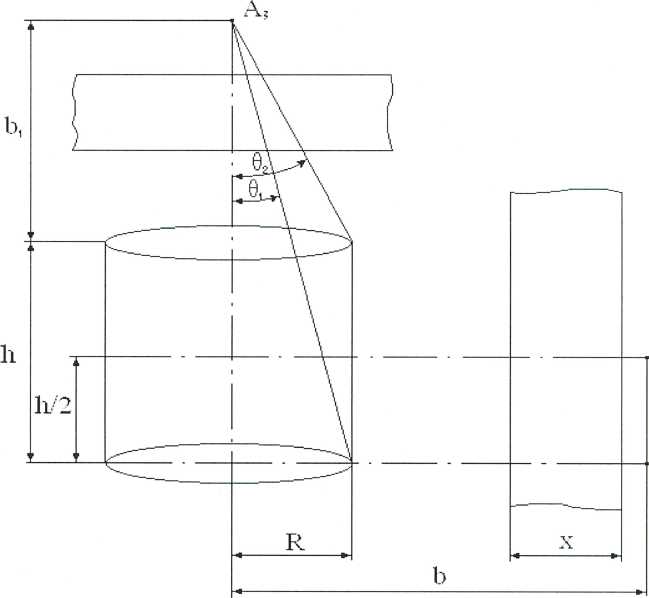
Рисунок 4.1.2.5.1 - цилиндрический источник с защитой
Первое слагаемое в выражении (4.1.2.5.3) соответствует значению мощности дозы от усеченного конуса, второе - мощности дозы от тела вращения, дополняющего усеченный конус до цилиндра

где θ1=  . .
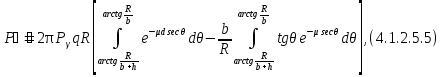
где θ2= 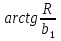 . .
Суммируя выражения для Р' и Р", получаем формулу для мощности дозы излучения, создаваемой непоглощающим цилиндрическим источником в точке, произвольно расположенной на его оси [7].
4.2 Инженерные методы расчета защиты от нейтронов
При рассмотрении расчета защиты от нейтронного излучения следует иметь в виду процессы взаимодействия нейтронов с веществом среды.
1. Защита от нейтронного излучения основывается на поглощении тепловых нейтронов. Быстрые нейтроны должны быть сначала замедлены.
2. Нейтроны с энергией свыше 0,5 МэВ рассеиваются на ядрах поглощающей среды, испытывая неупругие столкновения с выходом нейтронов меньшей энергии. При этом ядра переходят в возбужденное состояние и возвращаются в основное состояние, испуская γ- излучение или β- частицы.
3. Нейтроны, имеющие энергию до 0,5 МэВ, испытывают в основном упругое рассеяние.
В результате неупругого рассеяния нейтроны замедляются до тепловых и приходят в тепловое равновесие с окружающей средой. Тепловые нейтроны, диффундируя в защите, могут либо выйти за ее пределы, либо быть поглощены в самой защите. При этом возникает захватное γ - излучение, которое необходимо учитывать при расчете защиты.
4. Под действием нейтронного облучения многие материалы активируются. Это следует учитывать при выборе защиты.
Ослабление узкого моноэнергетического пучка быстрых нейтронов происходит по экспоненте
φx= φexp( ), (4.2.1) ), (4.2.1)
где φx – плотность потока нейтронов, нейтр./м2*с, после ослабления в защите толщиной x, см;
φ – плотность потока без защиты;
 полное макроскопическое сечение защитного материала, полное макроскопическое сечение защитного материала,  [1]. [1].
4.2.1 Описание инженерных методов расчета
Перенос нейтронов в общем виде описывается кинетическим уравнением Больцмана. Методы расчета поля нейтронов в защите, основанные на различных способах решения уравнения переноса, при практической реализации наталкиваются на серьезные трудности, связанные главным образом, со сложностью реальной геометрии защиты. Поэтому в инженерной практике широко используются упрощенные приемы решения задачи о переносе нейтронов в защите. Физической предпосылкой использования таких приемов является тот факт, что на достаточно большом расстоянии от источника плотность потока нейтронов может быть представлена двумя компонентами: проникающей, т.е. плотностью потока нейтронов, дошедших до точки наблюдения либо без взаимодействия, либо после таких взаимодействий, которые мало меняли их энергию и направление движения, и замедлившейся - плотностью потока нейтронов, претерпевших рассеяние вблизи точки наблюдения.
Для описания такого представления плотности потока нейтронов развит метод «выведение - диффузия». Также используют упрощенные методы расчета прохождения нейтронов через защиту. Это метод сечения выведения и метод длины релаксации.
4.2.2 Метод выведения – диффузии
Методы диффузии основаны на решении упрощенного кинетического уравнения Больцмана - уравнения диффузии. Для нейтронов тепловых энергии, уравнение будет иметь вид
 (4.2.2.1) (4.2.2.1)
где  – коэффициент диффузии; – коэффициент диффузии;
 – поток нейтронов; – поток нейтронов;
 сечение захвата; сечение захвата;
 – сечение деления; – сечение деления;
v – среднее число вторичных нейтронов на одно деление;
Алгоритмы расчета, основанные на описании ослабления плотности потока быстрых нейтронов с помощью экспериментальных сечений выведения или длин релаксации, а замедляющихся нейтронов - диффузионным многогрупповым способом, объединены общим названием «выведение - диффузия».
Использование приближения выведения для быстрых нейтронов заключается в замене сечения захвата в диффузионном уравнении экспериментальным сечением выведения из группы, исключающим переходы внутри группы при рассеянии на малые углы. Распределение быстрых нейтронов (для одномерной геометрии) при этом можно вычислить с помощью следующего выражения
 (4.2.2.2) (4.2.2.2)
где Fвыв(r0) – поток быстрых нейтронов, падающих на защиту;
r0 – радиус источника;
λ – длина релаксации быстрых нейтронов в защите;
r – координаты расчетной точки;
α - геометрический фактор (α=0 – для одномерной плоской, α=1– для одномерной цилиндрической, α=2–для одномерной сферической геометрии).
В общем случае для повышения точности расчетов вводят несколько групп выведения. Диффузионные потоки для одной группы выведения находятся решением уравнения вида

где  – диффузионный поток нейтронов j-ой группы; – диффузионный поток нейтронов j-ой группы;
 – сечение увода из j-ой диффузионной группы; – сечение увода из j-ой диффузионной группы;
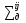 – сечение перехода из /-ой диффузионной группы в j-ую группу; – сечение перехода из /-ой диффузионной группы в j-ую группу;
 – сечение перехода из группы выведения в j-ую диффузионную – сечение перехода из группы выведения в j-ую диффузионную
группу.
Решив это уравнение, получают пространственно энергетическое распределение нейтронов замедления.
4.2.3 Метод длин релаксации
Длина релаксации - параметр, часто применяемый для расчета ослабления защитой нейтронов и γ - излучения. Она характеризует уменьшение величины потока, плотности энергии, биологической дозы и мощности дозы.
Анализ показывает, что пространственное распределение плотности потока нейтронов с достаточно хорошей для практических расчетов точностью после исключения геометрического ослабления удается описать простой экспоненциальной зависимостью вида
F(x) = F0 exp(–x/ L), (4.2.3.1)
где L – длина релаксации нейтронов в среде, в общем случае зависящая от энергии нейтронов источника, толщины слоя материала, компоновки и геометрии защиты, энергии детектируемых нейтронов и других условий измерений.
В большинстве случаев L не зависит от толщины защиты лишь в определенном диапазоне изменения х, поэтому ее определяют для отдельных участков защиты, в пределах которых ослабление нейтронов может быть описано экспоненциальной зависимостью с постоянным значением L. В таких случаях плотность потока нейтронов определяется по формуле

где т - число участков, на которое разбита защита по толщине;
 – толщина защиты i-го участка, для которого Lпринята равной Li. – толщина защиты i-го участка, для которого Lпринята равной Li.
В общем случае ход кривой ослабления на начальном участке на расстоянии от источника в 2-3 L может отличаться от экспоненциального. Это отличие можно учесть введением в зависимость вида (4.2.3.1) или (8.2.3.2) коэффициента f, характеризующего отклонение от экспоненциальной формы кривой ослабления на начальных расстояниях от источника. Для источников нейтронов деления часто  . .
С учетом коэффициента f плотность потока нейтронов, например, моноэнергетического точечного изотропного источника мощностью q0 за защитой толщиной х, когда источник и детектор находятся с разных сторон защиты, может быть определена из соотношения

Для немоноэнергетического источника со спектром вида р0(е0 )
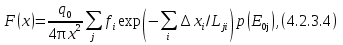
где  – доля нейтронов источника в энергетическом интервале от – доля нейтронов источника в энергетическом интервале от
E0j до E0j +Δ E0j;
fi – коэффициент для энергии E0j +Δ E0j/2;
Lji– длина релаксации для нейтронов энергией E0j +Δ E0j/2 на толщине защиты i-го участка [2].
|
|
|
 Скачать 152.77 Kb.
Скачать 152.77 Kb.