Расчет защит. Классификация источников излучения
 Скачать 152.77 Kb. Скачать 152.77 Kb.
|
|
3. КЛАССИФИКАЦИЯ ЗАЩИТЫ Материалы, располагаемые между источником излучения и зоной размещения персонала или оборудования для ослабления ионизирующего излучения, называют защитой. Защиту от ионизирующих излучений классифицируют по назначению, типу, компоновке, форме и геометрии. Защита от ионизирующих излучений должна обеспечивать: а) допустимый уровень облучения обслуживающего установку персонала; б) допустимый уровень радиационных повреждений конструкционных и защитных материалов; в) допустимый уровень радиационного энерговыделения и температурного распределения в конструкционных и защитных материалах. В соответствии с этим защиту подразделяют соответственно на биологическую, радиационную и тепловую. Радиационная и тепловая защиты, которые конструкционно часто бывают совмещены, необходимы только для мощных источников излучения ядерно-технических установок, таких, например, как ядерные реакторы. При работе с изотопными источниками необходимость в радиационной и тепловой защите обычно не возникает. Защиты подразделяются на следующие типы:
3) теневая защита устанавливается между источником излучения и защищаемой областью, размеры которой ограничиваются «тенью», отбрасываемой защитой, особенно часто такая защита используется при ограничениях ее массы и габаритов; 4)частичная защита – ослабленная защита для областей ограниченного доступа персонала (например, на судне с реактором в качестве энергетической установки частичная защита может осуществляться в направлении дна). По компоновке выделяют гомогенную (из одного защитного материала) и гетерогенную (из различных материалов) защиты. По форме внешней поверхности наиболее часто на практике встречается плоская, сферическая и цилиндрическая защиты. Если критерием классификации выбрать геометрию защиты, можно выделить следующие ее виды: бесконечная, полубесконечная, барьерная и ограниченная [2]. 4. ИНЖЕНЕРНЫЕ МЕТОДЫ РАСЧЕТА ЗАЩИТЫ Методы расчета защиты, основанные на различных способах решения кинетического уравнения переноса излучения, при практической реализации наталкиваются на значительные трудности. Эти трудности связаны и с большими затратами машинного времени при решении задачи на ЭВМ, и со сложностью геометрии защиты, для которой часто неправомерно использование точных методов, развитых для идеализированной геометрии, и с неточностями, которые возникают из-за погрешности имеющихся ядерных констант при описании глубокого проникновения излучения в защиту. В связи с этим широкое распространение, особенно на начальной стадии проектирования защиты и при проведении многовариантных расчетов, получили полуэмпирические методы расчета защиты, которые являются эффективным средством получения достаточно точной (хотя и ограниченной только некоторыми функционалами) информации о полях нейтронного и γ- излучений в защите. Разработанные в ранний период развития ядерной энергетики, эти методы, постоянно совершенствуясь, до настоящего времени не потеряли своего практического значения. Основными преимуществами полуэмпирических методов перед точными являются их простота, оперативность, небольшие затраты машинного времени ЭВМ (многие задачи допускают решение вручную), возможность решения задач со сложной геометрией [5]. 4.1 Инженерные методы расчета защиты от γ – излучения Для проектирования защиты от γ - излучения должны быть известны три фактора: интенсивность и энергия источников, от излучения которых проектируется защита, ослабление излучаемых γ- квантов выбранными материалами защиты и уровень, до которого необходимо снизить излучение. Процессы, в результате которых γ- излучение ослабляется в защите, хорошо известны, и, если только геометрия защиты не очень сложна, количество защитных материалов, необходимых для требуемого ослабления излучения, можно подсчитать достаточно точно. При измерениях полей γ - излучения в реальных задачах наряду с нерассеянным излучением источника регистрируют многократно рассеянные в среде γ - кванты. Под рассеянными понимаются кванты, претерпевшие однократное или многократное рассеяние. Геометрию, при которой учитывается нерассеянное и рассеянное излучение, называют геометрией широкого пучка («плохой» геометрией) [2]. 4.1.1 Факторы накопления При прохождении у- излучения через вещество создается широкий пучок излучения, состоящий из рассеянного и не рассеянного излучений. Интенсивность широкого пучка выражается формулой φω = φω0 exp(-µx) BЭ (Eγ, Z, µx), (4.1.1.1) где φω0 – интенсивность излучения без защиты; µ – линейный коэффициент ослабления; x – толщина защиты; BЭ (Eγ, Z, µx) – энергетический фактор накопления, учитывающий вклад рассеянного излучения. Энергетический фактор накопления зависит от энергии фотонов, атомного номера поглощающего вещества и длины свободного пробега. Энергетический фактор накопления показывает, во сколько раз увеличивается интенсивность излучения широкого пучка в сравнении с интенсивностью излучения узкого пучка за защитой. Фактор накопления может относиться к различным измеряемым параметрам у- излучения: числу фотонов (числовой фактор накопления); интенсивности излучения (энергетический фактор накопления); экспозиционной дозе излучения (дозовый фактор накопления) и поглощенной дозе излучения (фактор накопления поглощенной энергии). При рассмотрении влияния рассеянного излучения в зависимости от протяженности поглощающей среды, относительно которой распологаются источник и детектор, возможны различные варианты: 1) источник и детектор помещаются в бесконечной поглощающей среде (фактор накопления В∞); 2) источник находится в бесконечной поглощающей и рассеивающей среде, а детектор вне ее и наоборот, геометрия полубесконечная (фактор накопления B1/2∞); 3) источник и детектор разделены защитой поглощающей и рассеивающей средой с бесконечными поперечными размерами, барьерная геометрия - наиболее распространенный случай (фактор накопления Вб); 4) источник и детектор разделены защитной поглощающей и рассеивающей средой с конечными поперечными размерами, ограниченная геометрия – ограниченные барьерные среды, теневые защиты и др. (фактор накопления B0). При расчете защиты в условиях барьерной геометрии удобно пользоваться поправочными коэффициентами, представляющими отношение дозового фактора накопления в барьерной геометрии к дозовому фактору накопления в бесконечной среде для точечного изотропного источника, т.е. 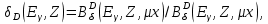 (4.1.1.2) (4.1.1.2)или отношение энергетического фактора накопления в барьерной геометрии к энергетическому фактору накопления в бесконечной среде для плоского мононаправленого источника, т.е. 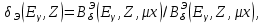 (4.1.1.3) (4.1.1.3)Тогда уравнение (8.1.1.1) при учете фактора накопления для барьерной геометрии будет выражаться следующей формулой: φω = φω0 exp(-µx) 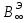 (Eγ, Z, µx) (Eγ, Z, µx)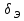 (Eγ, Z). (4.1.1.4) (Eγ, Z). (4.1.1.4)Численные значения факторов накопления были получены из решения интегро-дифференциального уравнения переноса для точечного изотропного и плоского мононаправленого источников для бесконечной гомогенной среды при различных параметрах Еγ, Z, µх. Для расчетов иногда представляют фактор накопления в виде суммы двух экспоненциальных членов B(Eγ, Z, µx)=A1 exp(-α1 µx) A2 exp(-α2 µx), (4.1.1.5) где α1, α2,Aα2=(1-A1) – численные коэффициенты, не зависящие от µx, они зависят от Eγ, Z. Несмотря на, то что законы, описывающие взаимодействие γ - излучения с веществом, хорошо известны и соответствующие сечения обычно определены экспериментально с точностью, достаточной для решения практических вопросов защиты, расчет факторов накопления и других величин, зависящих от многократного излучения, представляет еще до сих пор сложную проблему. Это является следствием специфической математической формы уравнения Клейна Нишины и в результате этого сложности члена комптоновского рассеяния в уравнении переноса. Интегро-дифференциальное уравнение, описывающее поведение γ- излучения в данном энергетическом интервале с направлением, лежащим в данном телесном угле, под которым они входят в элемент объема и выходят из него в единицу времени, не имеет точного решения, и для того чтобы решить его, разработан ряд приближенных методов расчета. Наиболее удобным считается метод моментов, или полиномиальный метод. Он позволяет рассчитывать поток многократно рассеянных γ- квантов в бесконечной среде как функцию энергии и глубины проникновения квантов и, таким образом, дает возможность рассчитать большинство необходимых факторов накопления. Метод моментов применяется при толщинах проникновения вплоть до 15 длин свободного пробега, и расчет проводится для интервала энергий от 10 МэВ и ниже вплоть до 100 или 50 кэВ. Если учесть, что излучение быстро ослабляется при низких энергиях (в результате фотоэффекта), то этот интервал энергий достаточен для практического применения. Наибольшие ошибки этого метода наблюдаются при самых больших глубинах проникновения и самых малых энергиях, но даже и в этих случаях спектр энергий и величины факторов накопления подсчитываются с точностью до 20 % [1], [6]. 4.1.2 Описание инженерных методов В основе большинства инженерных методов расчета прохождения γ- квантов через защиту лежит метод лучевого анализа (интегрирование функции влияние «точечного ядра»). Сущность метода лучевого анализа состоит в том, что источник γ - излучения представляют суперпозицией точечных источников, рассматривают один из точечных источников и анализируют ослабление излучения вдоль луча, соединяющего источник с точкой наблюдения. При решении задач прохождения γ- излучения через защиту первоначально рассматривается поле нерассеянных γ- квантов, ослабление которых происходит по экспоненциальному закону. Учет нерассеянного излучения в искомый функционал проводится с помощью фактора накопления γ - квантов [5]. 4.1.2.1 Защита от γ - излучения то точечных источников Характерным свойством точечного изотропного источника в непоглощающей и нерассеивающей среде является изменение поля излучения в обратной зависимости от квадрата расстояния источник – детектор. Расчет защиты от γ - излучения по кратности ослабления. При расчете защиты от излучения удобно применять универсальные таблицы, вычисленные на основании теории ослабления в веществе широкого пучка γ - излучения от точечного источника. Кратность ослабления (k) представляет собой отношение измеренной или рассчитанной экспозиционной дозы X (мощности экспозиционной дозы X1) без защиты к предельно допустимой экспозиционной дозе ХПДДА (X1ДМДА) той же точке за защитным экраном толщиной х; к определяется по формуле K(Eγ)=X/XПДДА=X1/X1ДМДА (4.1.2.1.1) При определении по универсальным таблицам необходимо знать толщину защиты данного материала x, см, или кратность ослабления k , и энергию γ- излучения Еγ, МэВ, [1]. Номограммы для расчета защиты. Принцип построения универсальных таблиц может быть использован также для построения графической зависимости кратности ослабления излучения от толщины защиты для γ - излучающих радионуклидов. В случае сложного спектра излучения с энергиями E0,1, Е0,2, …, Е0,т и абсолютными вкладами каждой линии по экспозиционной дозе n1, п2, ..., пт, расчетная кратность ослабления k(x) фиксированной толщиной экрана x может быть определена из соотношения 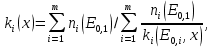 (4.1.2.1.2) (4.1.2.1.2)где парциальная кратность ослабления ki(E0,1,x) рассчитывается с помощью формул типа (4.1.2.1.1). Интегральную кратность ослабления можно получить экспериментально путем измерения мощности экспозиционной дозы после защитного экрана толщиной х. При этом должна соблюдаться геометрия широкого пучка, а измерения производиться ионизационными детекторами, имеющими малый ход с жесткостью. Тогда экспериментальная кратность ослабления будет k(x)=Pэкс(x=0)/Pэкс(x), (4.1.2.1.3) где Pэкс(x=0) – мощность экспозиционной дозы, измеренная в той же геометрии, но без экранов. Расчет по слоям половинного ослабления. Толщину защитного экрана, снижающую уровни излучения в два раза, называют слоем половинного ослабления Δ1/2 . Слой половинного ослабления Δ1/2 для моноэнергетического γ- излучения и источника со сложным спектром в широком пучке γ- излучения зависит от толщины защиты (с увеличением толщины защиты для моноэнергетического излучения уменьшается, для сложного спектра вначале увеличивается, а затем уменьшается), пропорциональной кратности ослабления. Поэтому в практических расчетах для быстроты определения примерной толщины защиты можно использовать приближенное значение слоя половинного ослабления γ- излучения в геометрии широкого пучка. Так, для 60Со и других γ- излучателей значения Δ1/2 будутравны: для свинца 1,3 см, для железа 2,4 см, для бетона 6,4 см. При известной кратности ослабления x можно определить число слоев половинного ослабления п и, следовательно, защиту. Зависимость между k и п имеет вид k=2n [1], [2]. |
