Классификация анализа экономики. Тема 2. КЛАССИФИКАЦИЯ ПРИЕМОВ И СПОСОБОВ ЭКОНОМИЧЕСКОГО АНАЛИЗА.. Классификация приемов и способов экономического анализа
 Скачать 196.1 Kb. Скачать 196.1 Kb.
|
|
Обоснование уравнения связи делается с помощью сопоставления параллельных рядов, группировки данных и линейных графиков. Размещение точек на графике покажет, какая зависимость образовалась между изучаемыми показателями – прямолинейная или криволинейная. Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой: 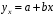 , ,где x – факторный показатель; 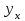 – результативный показатель; – результативный показатель; a и b – параметры уравнения регрессии, которые требуется определить. Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание значений результативного показателя. Значения коэффициентов a и bнаходят из системы уравнений, полученных по способу наименьших квадратов. В данном случае система уравнений имеет следующий вид: 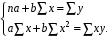 Коэффициентa – постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр bпоказывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения. Используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т. е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. Однако регрессионный анализ не дает ответа на вопрос, тесная это связь или нет, решающее воздействие оказывает данный фактор на величину результативного показателя или второстепенное. Для измерения тесноты связи между факторными и результативными показателями используется коэффициент корреляции. В случае прямолинейной формы связи между изучаемыми показателями коэффициент корреляции, r, рассчитывается по следующей формуле: 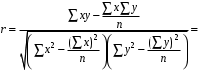 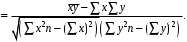 Коэффициент корреляции может принимать значения от 0 до ± 1. Чем ближе его величина к единице, тем более тесная связь между изучаемыми явлениями, и наоборот, знак показывает направление связи между фактором и результативным показателем. Чтобы установить, насколько тесной является связь при криволинейной форме зависимости, используется не линейный коэффициент корреляции, а корреляционное отношение: 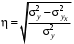 , ,где 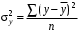 ; ; 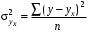 . .Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления. Многофакторный корреляционный анализ состоит из нескольких этапов. На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные из них для корреляционного анализа. На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т. е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. На пятом этапе дается статистическая оценка результатов корреляционного анализа и предлагается способ их практического применения. Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. Важное значение при отборе факторов имеют и теория и практика. При этом необходимо придерживаться следующих правил. 1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла. 2. При создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет. 3. Все факторы должны быть количественно измеримы, т. е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности. 4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер. 5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа. 6. Нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер. Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. Первые два этапа включают в себя сбор и статистическую оценку исходной информации, которая будет использоваться при корреляционном анализе. Собранная исходная информация должна быть проверена на точность, однородность и соответствие закону нормального распределения. В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неправильным результатам анализа и неправильным выводам. Одно из условий корреляционного анализа – однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации. Критериями однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической величины. Оно определяется по формуле: 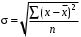 . .Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической. Он рассчитывается по формуле: 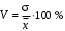 . .Следующий этап корреляционного анализа – расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, оказывающий наиболее значимое влияние на результативный показатель, потом второй, третий и т. д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, F-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи: 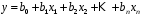 . .Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бета-коэффициентами по символу, который принят для их обозначения ( 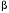 ). ). Бета-коэффициенты и коэффициенты регрессии связаны следующим отношением: 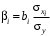 . .Бета-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бета-коэффициентов позволяет сделать вывод о сравнительной степени воздействия каждого фактора на величину результативного показателя. По аналогии можно сопоставить и коэффициенты эластичности, которые рассчитываются по формуле: 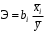 . .Коэффициенты эластичности показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1 %. Чтобы убедиться в точности (надежности) уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( 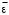 ), коэффициенты множественной корреляции (R) и детерминации (Д). ), коэффициенты множественной корреляции (R) и детерминации (Д). Критерий Фишера рассчитывается следующим образом: 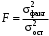 , ,где 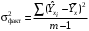 – факторная дисперсия; – факторная дисперсия;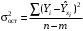 – остаточная дисперсия; – остаточная дисперсия;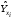 – индивидуальные значения результативного показателя, рассчитанные по уравнению; – индивидуальные значения результативного показателя, рассчитанные по уравнению;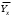 – среднее значение результативного показателя, рассчитанное по уравнению; – среднее значение результативного показателя, рассчитанное по уравнению;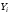 – фактические индивидуальные значения результативного показателя; – фактические индивидуальные значения результативного показателя;m – количество параметров в уравнении связи с учетом свободных членов уравнения; n – количество наблюдений. Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надежности связи. Если 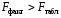 , то гипотеза об отсутствии связи между результативным показателем и исследуемыми факторами отклоняется. , то гипотеза об отсутствии связи между результативным показателем и исследуемыми факторами отклоняется.Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации:   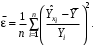 Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше средняя ошибка аппроксимации. О полноте связи можно судить также по величине множественных коэффициентов корреляции (R) и детерминации (Д): 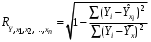 ; ;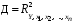 . .После проверки надежности рассчитанного уравнения регрессии делается вывод о возможности его использования на практике: 1. Для оценки результатов хозяйствования путем сравнения фактической величины результативного показателя с теоретической (расчетной), которая определяется на основе уравнения множественной регрессии. Если 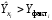 , то это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия. , то это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия.2. Для расчета влияния факторов на прирост результативного показателя 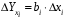 , ,где 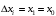 ; ;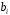 – коэффициент уравнения регрессии. – коэффициент уравнения регрессии.3. Для подсчета резервов повышения уровня исследуемого показателя ( 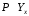 ) на величину соответствующего коэффициента регрессии ) на величину соответствующего коэффициента регрессии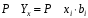 , ,где 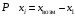 . .4. Для прогнозирования и планирования уровня результативного показателя. С этой целью необходимо в полученное уравнение связи подставить плановый (прогнозный) уровень факторных показателей. Таким образом, многофакторный корреляционный анализ имеет важную научную и практическую значимость. Он позволяет изучить закономерности изменения результативного показателя в зависимости от поведения разных факторов, определить их влияние на величину результативного показателя, установить, какие из них являются основными, а какие второстепенными. Этим достигается более объективная оценка деятельности предприятия, более точное и полное определение внутрихозяйственных резервов. Литература: Комплексный анализ хозяйственной деятельности: учебник и практикум для студентов, обучающихся по экономическим направлениям и специальностям и направлению "Экономика" / [В. И. Бариленко и др.] ; под редакцией В. И. Бариленко ; Финансовый университет при Правительстве Российской Федерации. - Москва: Юрайт, 2015. - 455 с. Савицкая Г.В. Экономический анализ: Учебник. - 14-е изд., перераб. и доп. - М. : Инфра-М, 2016. - 649 с. – (Высшее образование: Бакалавриат). |
