Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры
 Скачать 7.1 Mb.
|
Повторные независимые испытания. Формула Бернулли с выводом. ПримерыЕсли вер-ть наступления события А в каждом испытании не меняется в завис-ти от исходов других, то такие испытания наз-ся независ-ми относит-но события А. Если независ-е повторные испытания проводятся при одном и том же комплексе условий, то вер-ть наступления соб-я А в каждом испытании одна и та же. Последовательность испытаний, в кот 1 и те же события происходят с одинаковой вер-ю, назпоследовательностью независ-х испытаний. А соб, кот может иметь место с вер-ю Р(А) в любом из n испытаний. А ->P(A) P(A)=P – вер-ть осущ-я события в каждом отдельном событии  - вер-ть неоосущ-я событий;  ;  ;  Поставим задачу опр-я вер-ти m-кратного осуществл-я события А в серии из n испытаний. Pm,n – вер-ть m-кратного осуществл-я события в серии n испытаний. Условно рез-ты послед-ти независ-х испытаний м\б представлены:  , тк в послед-ти независ-х испытаний, каждое из соб независимо и для m-кратного осуществл события они должны произойти совместно, соотв-я вер-ть опр-ся по ф-ле вер-ти произведения  . Предполагая, что возможен и др порядок следования А и  на множестве n испытаний, а кол-во комбинаций =  , получим ф-лу m-кратного осуществ-я соб А в серии из n испытаний:  Формула Бернулли. Используется при усл, что соб происх-т многократно.Теорема: Если вер-ть А в каждом испытании постоянна, то вер-ть Pm,n того, что событие А наступит m раз в n независимых испытаниях, равна , где q=1-p ф Бернулли применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики.  Пример:  8.Локальная теорема Муавра-Лапласа, условия её применимости. Свойство функции f(x). Пример.   9. Асимптотическая формула Пуассона и условия её применимости. Пример Вычисление вероятности Pm,n появления события A при большом числе испытаний п по формуле Бернулли затруднительно. Возникает вопрос о нахождении формул, с помощью которых вероятность Pm,n можно вычислить приближенно. Такие формулы называют асимптотическими. Наиболее простой из них является формула Пуассона. Теорема(теорема Пуассона).Если вероятность р наступления события A в каждом испытании стремится к нулю при неограниченном увеличении числа испытаний п, причем произведение np стремится к постоянному числу l, то вероятность Pm,n того, что событие А наступит m раз в п независимых повторных испытаниях, приближенно равна  10. Интегральная теорема Муавра-Лапласа и условия её применимости. Функция Лапласа F(x) и её свойства. Пример.    11. Следствия из интегральной теоремы Муавра-Лапласа (с выводом). Примеры.     12. Понятие «случайная величина» и ее описание. Дискретная случайная величина и ее закон (ряд) распределения. Независимые случайные величины. Примеры.    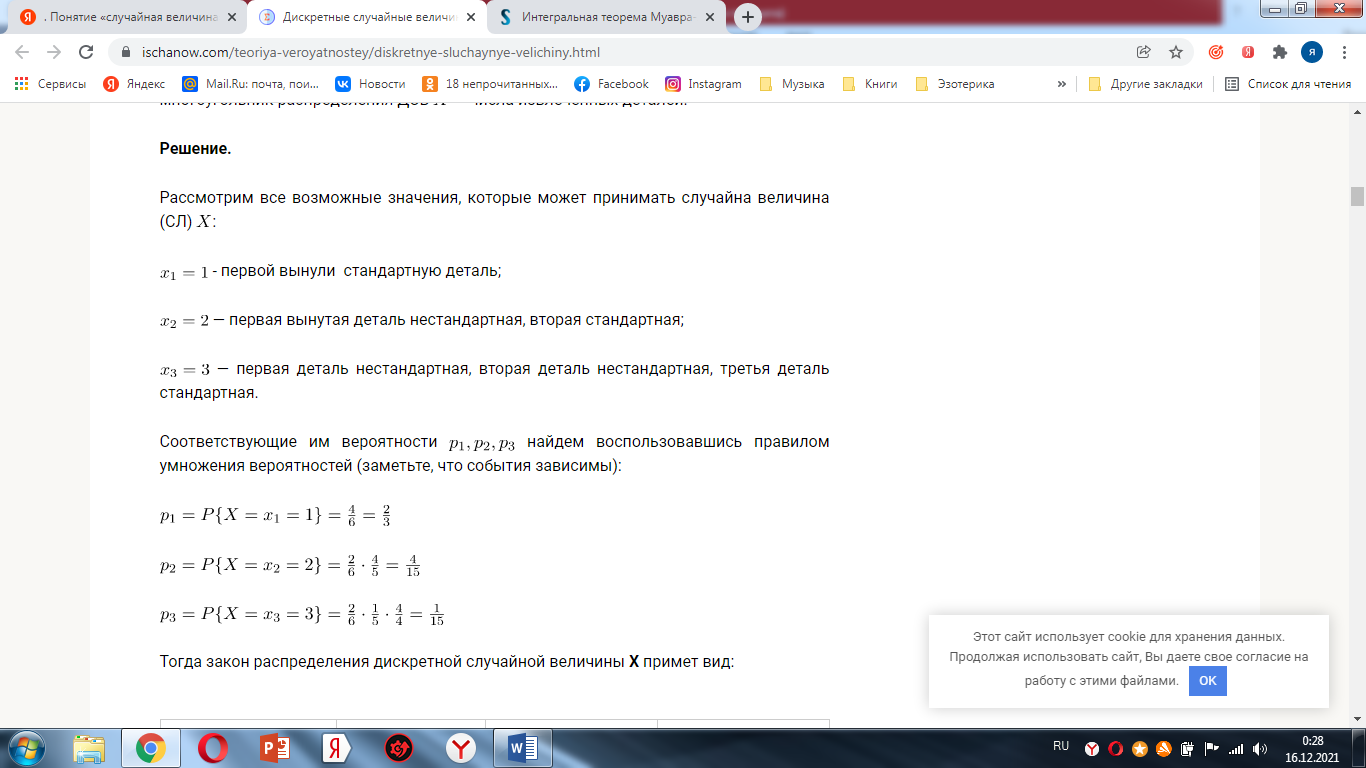 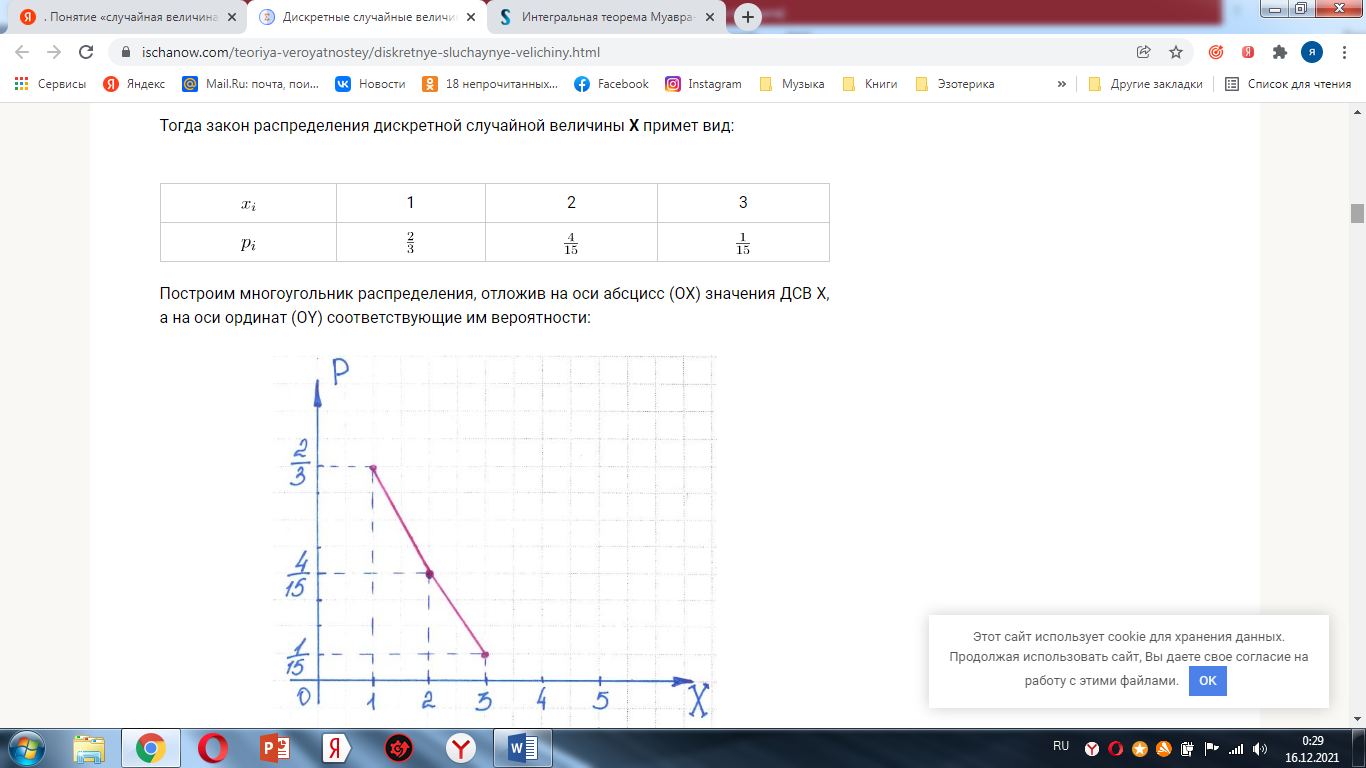 13. Математические операции над дискретными случайными величинами и примеры построения законов распределения для КХ,Х'1, X + К, XV по заданным распределениям независимых случайных величин X и У. 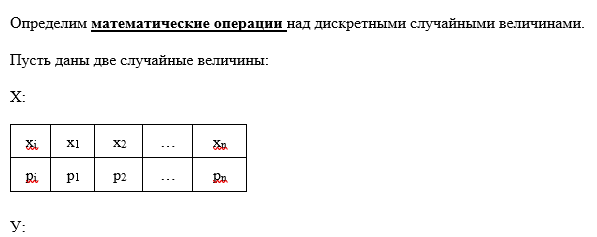   14. Математическое ожидание дискретной случайной величины и его свойства (с выводом). Примеры.    15. Дисперсия дискретной случайной величины и ее свойства (с выводом). Примеры. Дисперсией (рассеиванием) D ( X ) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Свойства дисперсии дискретной случайной величины1. Дисперсия дискретной случайной величины равна разности между математическим ожиданием квадрата величины и квадратом ее математического ожидания:  2. Дисперсия постоянной величины равна нулю. Действительно,  3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:  4. Дисперсия суммы двух независимых случайных величин и равна сумме дисперсий этих величин:  5. Дисперсия разности двух независимых случайных величин и равна сумме их дисперсий:  |