Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры

• Название: Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчёт вероятности. Примеры
• Дата: 01.02.2022
• Размер: 7.1 Mb.
• Имя файла: analiz_dannykh.docx
• Тип: Документы; #348213
• страница: 3 из 4

Пример 1.

Используя свойство 1 дисперсии, найдем дисперсию случайной величины   имеющей следующий закон распределения: 

Находим математические ожидания случайной величины   и ее квадрата: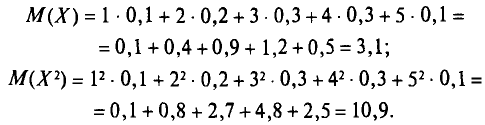



Отсюда в силу свойства 1 дисперсии



16. Математическое ожидание и дисперсия числа и частости наступления события в n повторных независимых испытаниях (с выводом).

Математическое ожидание и дисперсия числа т и частости появлений события при n повторных независимых испытаниях могут быть также вычислены и по формулам:

 .

 .

Теорема 1. Математическое ожидание случайной величины Х, распределенной по биномиальному закону, равноM(X)=np, а ее дисперсия равнаD(X)=npq.

Следствие. Математическое ожидание частости события вnнезависимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, равно p, то есть  , а ее дисперсия рана   .
17. Случайная величина, распределенная по биноминальному закону, ее математическое ожидание и дисперсия. Закон распределения Пуассона.

Биномиальным называется распределение случайной величины, в котором она принимает последовательность целых неотрицательных значений с вероятностями определяемыми по формуле Бернулли. 

Математическое ожидание   и дисперсия   биномиально распределённой случайной величины.

Законом распределения Пуассона называется распределение случайной величины, в которой она принимает последовательность целых неотрицательных значений с вероятностями, определяемыми по формуле Пуассона. Математическое ожидание находится , а дисперсия 

Распределение Пуассона. Пусть производится n независимых испытаний, в котором появление события А имеет вероятность р. Если число испытаний n достаточно велико, а вероятность появления события А в каждом испытании мало, то для нахождения вероятности появления события А k раз находится следующим образом: Произведение np сохраняет постоянное значение:  , это означает, что среднее число появления события в различных сериях испытаний (при разном n) остается неизменным.

По формуле Бернулли получаем:

; 

+ Найдем предел этой вероятности при n ∞.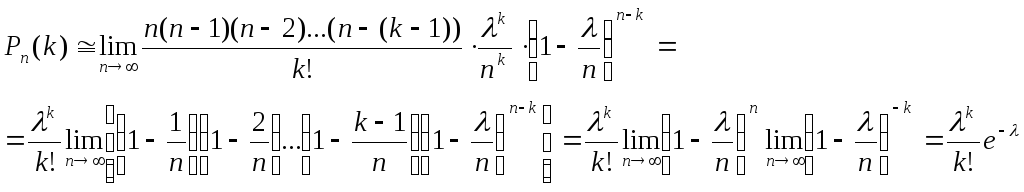



Получаем формулу распределения Пуассона: 

18. Функция распределения случайной величины, ее определение, свойства и график.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X  в результате испытания примет значение, меньшее x, то есть:



Функцию распределения дискретной случайной величины  можно представить следующим соотношением: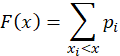



Это соотношение можно переписать в развернутом виде: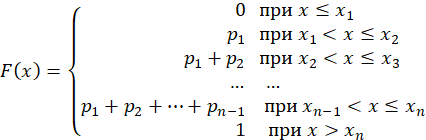



Функция распределения дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции  равна 1.

Свойства функции распределения

Свойство 1.

Значения функции распределения принадлежат отрезку [0;1]:



Свойство 2.

F(x) – неубывающая функция, то есть:

, если x₂>x₁

Свойство 3.

Если возможные значения случайной величины принадлежат интервалу (a,b), то:

1)  F(x)=0 при

2)  F(x)=1 при 

Свойство 4.

Справедливо равенство:



Свойство 5.

Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый.

Свойство 6.

Если возможные значения непрерывной случайной величины расположены на всей оси x, то справедливы следующие предельные соотношения:





Свойство 7.

Функция распределения непрерывная слева, то есть: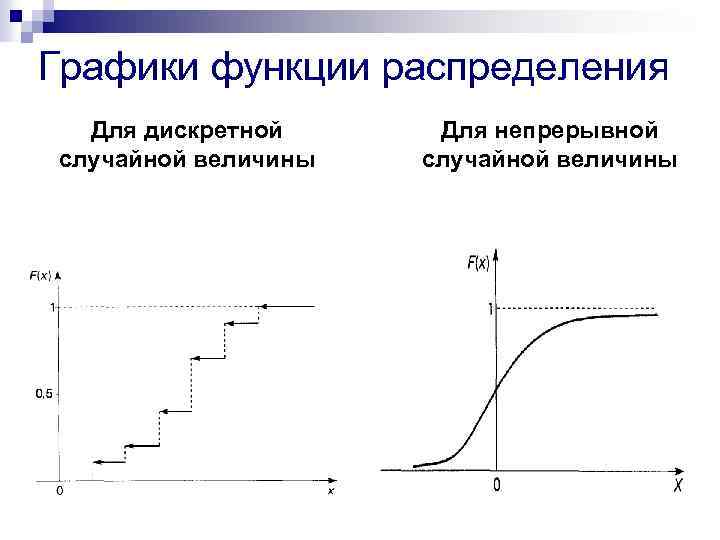




19. Непрерывная случайная величина (НСВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия НСВ.

Случайная величина Х называется непрерывной, если её Функция Распределения непрерывна в любой точке и дифференцируемая всюду, кроме отдельных точек (точки излома).

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайных величин на их вероятности.

 Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.

Математическим ожиданием НСВ Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл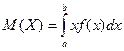   

Если возможные значения случайных величин рассматриваются на всей числовой оси, то математическим ожиданием определяется по формуле:   , при этом предполагается, что несобственный интеграл сходится.

Дисперсией НСВ является математическое ожидание квадрата ее отклонения.   

По аналогии для практического вычисления дисперсии:   .

Математическое ожидание определяется: 

   ,если интеграл абсолютно сходится и   

Дисперсии имеет вид:   или 

Функция распределения НСВ:

 

Основные свойства функции распределения НСВ:

С1.

С2.

С3. 

С4. 1)   

2) 



Плотностью распределения  НСВ Х называется производной её функции распределения 

Свойства плотности распределения:

С1.  ;

С2.  

С3.

С4.

Плотность вероятности существует только для НСВ. График плотности вероятности называется кривой распределения.

20. Плотность вероятности непрерывной случайной величины, ее определение, свойства и график.

Плотностью вероятности (плотностью распределения или просто плотностью)  непрерывной случайной величины Х называется производная ее функции распределения

Свойства плотности вероятности непрерывной случайной величины.

1. 
   Плотность вероятности - неотрицательная функция, т.е.  .
   

как производная монотонно неубывающей функции F(х).

2. 
   Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b
   
3. 
   Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:
   
4. 
   Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:  .
   

Свойства 1 и 4 плотности вероятности означают, что график - кривая распределения - лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.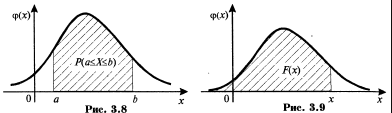



21. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров.

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и  , если ее плотность вероятности имеет вид: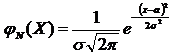

Кривую нормального закона распределения называют нормальной. На рисунках а, б приведены нормальная кривая  с параметрами а и , т.е. , и график функции распределения случайной величины Х, имеющей нормальный закон.

Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=а, имеет максимум в точке х=а, равный  , т.е. , и две точки перегиба с ординатой .

Рассмотрим теорему, устанавливающую теоретико-вероятностный смысл параметров нормального закона.

Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е.  , а ее дисперсия - параметру  , т.е.  .

Выясним, как будет меняться нормальная кривая при изменении параметров а и  (или ). Если , и меняется параметр а ( ), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 4.6).

Ес ли a=const и меняется параметр (или ), то меняется ордината максимума кривой . При увеличении ордината максимума кривой уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении а, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков. На рис. 4.7 показаны нормальные кривые с параметрами , где . Т.о., параметр а (он же математическое ожидание) характеризует положение Центра, а параметр  (он же дисперсия) -форму нормальной кривой.

22. Функция распределения нормально распределенной случайной величины и её выражение через функцию Лапласа.

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, и вероятности ее попадания на некоторый промежуток связана с тем, что интеграл является «неберущимся». В элементарных функциях. Поэтому их выражают через функцию:

.

Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-х; х] (рис. 4.8).



Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

.

По формуле  функция распределения: .

Сделаем замену переменной, полагая  , , при , , поэтому

.

Первый интеграл

.

(В силу четности подынтегральной функции и того, что интеграл Эйлера-Пуассона равен  ).

Второй интеграл с учетом   составляет  .

Итак,  .
23. Формулы для определения вероятности:

а) попадания нормально распределенной случайной величины в заданный интервал;

б) ее отклонения от математического ожидания. Правило «трех сигм».
1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал  , равна  ,

Где  , .

□ Учитывая, что вероятность  есть приращение функции распределения на отрезке и учитывая формулу получим:

.

2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину  (по абсолютной величине), равна  , где  .

□  . Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим

«правило трех сигм»:

Если случайная величина Х имеет нормальный закон распределения с параметрами а и  , т.е. N(a; ), то практически достоверно, что ее значения заключены в интервале ( ).

Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на  (по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:

.

24. Неравенство Маркова (лемма Чебышева) (с выводом). Пример.





25. Неравенство Чебышева (с выводом) и его частные случаи для случайной величины, распределенной по биномиальному закону, и частости события.

Теорема. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:  ,

где а = М(Х), е > 0.

Применим неравенство Маркова в форме   к случайной величине  , взяв в качестве положительного числа  . Получим:  .

Т.к. неравенство  равносильно неравенству , а  есть дисперсия случайной величины Х, то из неравенства получаем доказываемое неравенство. ☻

Учитывая, что события  и   противоположны, неравенство Чебышева можно записать и в другой форме:  .

Неравенство Чебышева применимо для любых случайных величин. В форме   оно устанавливает верхнюю границу, а в форме   - нижнюю границу вероятности рассматриваемого события.

Запишем неравенство Чебышева в форме   для некоторых случайных величин:

а) для СВ Х = m, имеющей биноминальный закон распределения с математическим ожиданием а = М(Х) = nр и дисперсией D(X) = npq:  .

б) для частости   события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью   и имеющей дисперсию  :  .

3амечание. Если М(Х) > А или  , то правые части неравенств Маркова и Чебышева в форме соответственно   и   будут отрицательными а в форме   и   будут больше 1.

Это означает, что применение указанных неравенств в этих случаях приведет к тривиальному результату: вероятность события больше отрицательного числа либо меньше числа, превосходящего 1.
26. неравенство Чебышева для средних арифметических случайных величин (с выводом).





27. теорема Чебышева (с доказательством), ее значение и следствие. Пример.

 Если дисперсии n независимых случайных величин   ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий  , т.е.







Следствие: Если независимые случайные величины   имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то:.



Пример:



Значение:

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов.

28. закон больших чисел. Теорема Бернулли ( с док-ом) и ее значение. Пример.





Значение: когда речь идет о больших числах, данная теорема помогает легко найти решение.

Пример:

29. центральная предельная теорема. Понятие о теореме Ляпунова и ее значение. пример.
Теорема Ляпунова: если случайная величина   представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то   имеет распределение близкое к нормальному.

Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом.





30. вариационный ряд и его разновидности. Средняя арифметическая и дисперсия ряда., упрощенный способ их расчета.

Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами или частостями). При этом вариантами называются различные значения случайной величины Х.

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину.

Вариационный ряд называется непрерывным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину.

Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами, а их отношения к общему числу наблюдений – частостями (или относительными частотами).

Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:



Дисперсией s² вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:



Дисперсию s² часто называют эмпирической или выборочной, отмечая, что она находится по опытным или статистическим данным.

Вычисление средней арифметической и дисперсии вариационного ряда можно упростить, если использовать не первоначальные варианты x_i, а новые варианты   , где c и k специально подобранные постоянные.

Средняя арифметическая может быть вычислена по формуле:



Дисперсия может быть вычислена по формуле:

 .

31. генеральная и выборочная совокупности. Принцип образования выборки. Собственно- случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.

Генеральной совокупностью называется вся подлежащая изучению совокупность объектов.

Выборочной совокупностью (или выборкой) называется та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности объектов.

Числа объектов (наблюдений) в генеральной или выборочной совокупности называются их объемами.

Выборка должна быть отобрана случайно. Случайность достигается соблюдением принципа равной возможности всем элементам генеральной совокупности быть отобранными в выборку (жеребьевка; использование случайных чисел).

Виды выборок:

- собственно-случайная выборка (образовывается случайным выбором элементов без расчленения на части и группы);

- механическая выборка;

- стратифицированная выборка;

- серийная выборка.

Два способа образования выборок:

- повторный отбор (случайно отобранный и обследованный элемент возвращается в общую совокупность и может быть повторно отобран);

- бесповторный отбор (отобранный элемент не возвращается в общую совокупность).

Выборка называется репрезентативной, если она достаточно хорошо воспроизводит генеральную совокупность.

Сущность выборочного метода состоит в том, чтобы по некоторой выборке судить о генеральной совокупности в целом (преимущества и недостатки выборочного метода).

Основной задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.

В дальнейшем используем обозначения:

x_i – значения признака;

N и n – объемы генеральной и выборочной совокупностей;

N_i и n_i – число элементов генеральной и выборочной совокупностей со значением признака x_i;

M и m – число элементов генеральной и выборочной совокупностей, обладающих данным признаком.

Выборочный метод широко применяется на практике. Однако значение этой темы значительно шире, поскольку концепция выборки лежит в основе методологии математической статистики. Соотношение между характеристиками выборочной и генеральной совокупностей есть соотношение между опытными данными (результатами наблюдений) и теоретической моделью.

32. понятие об оценке параметров генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.

На практике редко встречается ситуация, когда изучаемый закон распределения неизвестен полностью. Чаще вид закона распределения известен заранее (из теоретических соображений) и требуется найти только неизвестные параметры, от которых он зависит (l в распределении Пуассона; a и s² для нормального распределения и т.д.).

Более того, в некоторых задачах сам закон распределения не существен, а требуется найти только его числовые характеристики.

В связи с этим возникает следующая задача: по известным значениям x₁, x₂, ¼ , x_n случайной величины Х, полученным в результате n независимых опытов, оценить значение некоторого параметра Q закона распределения случайной величины Х.

Ясно, что любая оценка для Q (обозначим ее  ) представляет собой некоторое выражение, зависящее от x₁, x₂, ¼ , x_n , т.е.  . Таким образом, сама оценка  является случайной величиной, зависящей как от закона распределения случайной величины Х, так и от числа опытов n.

Свойства оценок:

1. Оценка  называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.  ;

2. Оценка  называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:  ;

3. Несмещенная оценка  параметра Q называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра Q, вычисленных по выборкам одного и того же объема n.

33. оценка генеральной доли по собственно-случайной выборке. Несмещенность и состоятельность выборочной доли.

Пусть генеральная совокупность содержит N элементов, из которых M элементов обладает некоторым признаком А. Необходимо найти оценку генеральной доли  . В качестве такой возможной оценки параметра р рассмотрим его статистический аналог – выборочную долю  .

Теорема 1. Выборочная доля  повторной выборки является несмещенной и состоятельной оценкой генеральной доли  , причем ее дисперсия  , где q=1-p.

Доказательство. Математическое ожидание и дисперсия частости события в n независимых повторных испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p , равны соответственно M(w)=p, D(w)=s_w²=pq/n . Из первого равенства следует, что выборочная доля w есть несмещенная оценка генеральной доли р; из второго равенства получаем ее дисперсию.

Состоятельность оценки  следует непосредственно из теоремы Бернулли  , или  .

Теорема 2. Выборочная доля  бесповторной выборки является несмещенной и состоятельной оценкой генеральной доли  , причем ее дисперсия  , где q=1-p.

34. оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней.

Пусть из генеральной совокупности объема N отобрана случайная выборка Х₁, Х₂, … , Х_k, … , Х_n , где Х_k ¾ случайная величина, выражающая значение признака у k-го элемента выборки. Необходимо найти оценку генеральной средней. В качестве такой возможной оценки рассмотрим его статистический аналог – выборочную среднюю  .

Теорема 1. Выборочная средняя  повторной выборки является несмещенной и состоятельной оценкой генеральной средней  , причем ее дисперсия  .

Доказательство. Математическое ожидание выборочной средней  :

, т.е.  – несмещенная оценка для  .

Дисперсия выборочной средней  :

.

Состоятельность оценки  следует непосредственно из теоремы Чебышева.

Теорема 2. Выборочная средняя  бесповторной выборки является несмещенной и состоятельной оценкой генеральной средняя  , причем  .

35. оценка генеральной дисперсии по собственно- случайной выборке. Смещенность и состоятельность выборочной дисперсии. Исправленная выборочная дисперсия.