Компьютерные сети. Принц, техн, прот 1-303. Книга переведена на английский, испанский, китайский и португальский языки
 Скачать 5.49 Mb.
|
|
Начальное значение фазы ср показывает сдвиг синусоиды относительно начала точки отсчета времени, влево – при положительном значении фазы и вправо – при отрицательном. Выше мы рассматривали синусоиду как функцию времени y(t) в некоторой фиксированной точке пространства. Однако можно использовать другое представление синусоидальной функции у(х), когда ее значения изменяются в зависимости от расстояния х от некоторой точки. В реальной жизни мы часто сталкиваемся именно с такой природой колебательных процессов, когда колебания способны перемещаться, удаляясь от места возникновения. Синусоида как функция времени составляет единое целое с синусоидой функции расстояния, то есть является функцией двух переменных y(t, х), что отражает взаимосвязь временной и пространственной периодичности. У синусоиды у(х) имеется параметр – длина волны, который является аналогом периода синусоиды y(t).Длина волны (X) определяется как расстояние, на которое перемещается волна за время, равное периоду Г, и, таким образом, скорость распространения волны v в данной среде равна и = 'к/Т. В вакууме все электромагнитные волны распространяются со скоростью, равной 300 000 км/с, независимо от их частоты. Эта скорость с (си) называется скоростью света. Таким образом, для вакуума справедливо фундаментальное соотношение с = к/Тили с = X/. 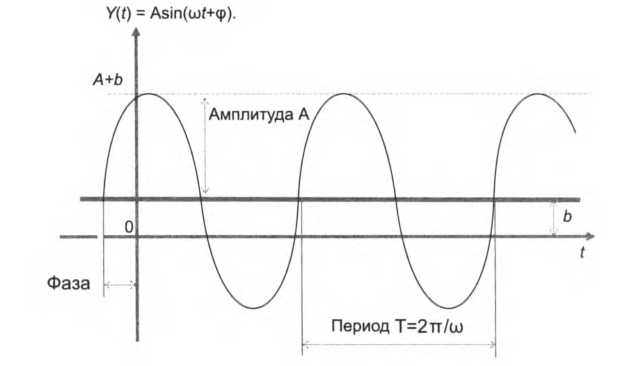 Синусоидальные функции обладают многими свойствами, делающими их эффективным инструментом изучения сигналов и линий связи. Одной из таких особенностей, например, является связанный с ними развитый математический аппарат. Поэтому такую важность приобретает факт, что процесс, описываемый произвольной, не обязательно синусоидальной функцией, может быть представлен в виде некоторого набора синусоидальных функций. 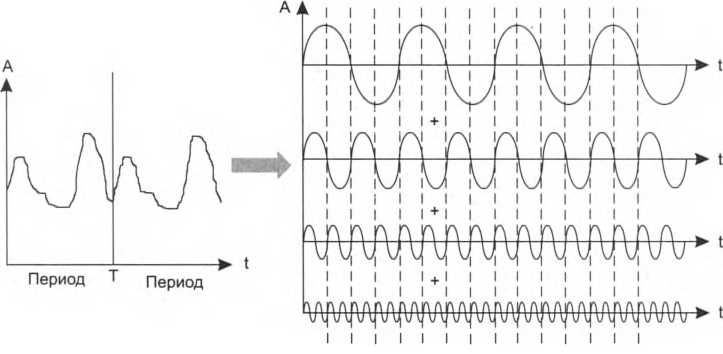 Рис. 6.5. Представление периодического аналогового сигнала суммой синусоид 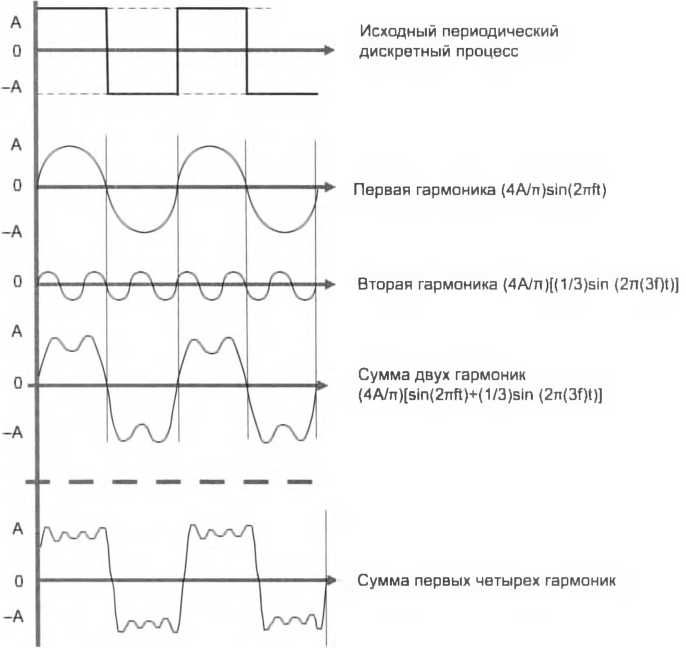 Рис. 6.6. Разложение и восстановление прямоугольных импульсов на основе спектрального представления Импульсные сигналы, наряду с другими способами кодирования дискретных компьютерных данных, часто используются в каналах связи, поэтому их спектральное разложение представляет для нас особый интерес. На рис. 6.6 показан периодический дискретный сигнал – последовательность прямоугольных импульсов. Этот сигнал может быть представлен суммой бесконечного числа синусоид, причем каждая из последующих имеет меньшую амплитуду и период. На рисунке мы видим две первые гармоники. Если их просуммировать, то в результате можно увидеть последовательность искаженных, но вполне распознаваемых прямоугольных импульсов. Еще ближе к исходному сигналу результат суммирования первых четырех гармоник. Отдельные гармоники можно представлять либо в виде синусоидальных функций от времени/расстояния, как это показано на рис. 6.6, либо в виде точек в координатах «частота – амплитуда», как на рис. 6.7 (здесь также изображен спектр последовательности прямоугольных импульсов). 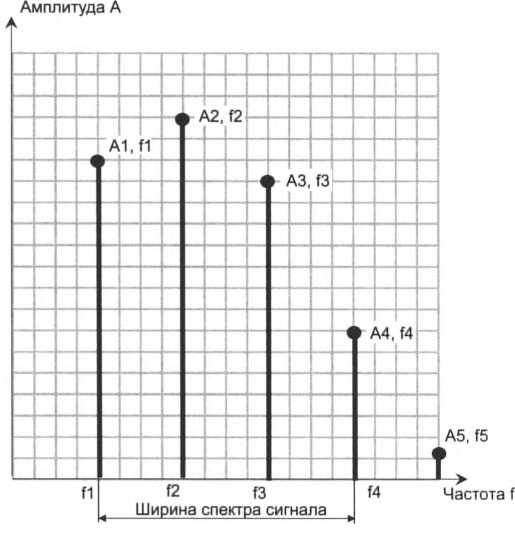 Непериодические процессы также можно представить в виде бесконечного ряда синусоидальных сигналов. Для сигналов произвольной формы, встречающихся на практике, спектр можно найти с помощью специальных приборов – спектральных анализаторов, которые измеряют спектр реального сигнала и отображают амплитуды составляющих гармоник на экране (рис. 6.8), распечатывают их на принтере или передают для обработки и хранения в компьютер в оцифрованном виде. 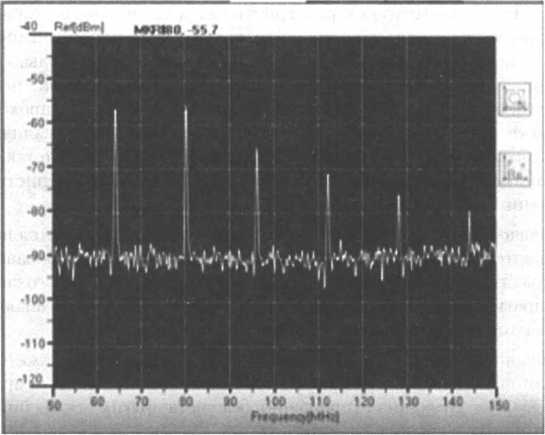 Затухание и опорная мощность Разложение произвольного информационного сигнала на гармоники дает нам возможность теоретически предсказать его изменение (искажение) при прохождении среды передачи данных, а это очень важно при проектировании линий связи, в процессе которого нужно выбрать передающую среду (например, медный проводник, оптическое волокно или радиоволны), способ кодирования информации, мощность передатчика, чувствительность приемника. Это предсказание основывается на следующем замечательном свойстве синусоидального сигнала – при прохождении через однородную распределенную в пространстве среду он сохраняет свою синусоидальную форму и частоту, а изменяются только его амплитуда и фаза. Следовательно, если мы будем знать, как некоторая среда передает синусоиды различной частоты, то сможем предсказать, как эта среда передаст любой периодический сигнал. Таким образом, не придется тестировать некоторую среду каждый раз, когда мы решим применить сигнал некоторой новой формы – достаточно будет найти разложение Фурье для нового сигнала и, зная, как среда передает гармоники, просуммировать или проинтегрировать их, получив результирующий сигнал на выходе среды. Вывод: зависимость амплитуды передаваемых гармоник от частоты для определенной среды должна быть найдена только один раз, а затем ее можно применять для анализа передачи различных типов сигналов этой средой. Для нахождения этой зависимости необходимо протестировать данную среду набором эталонных синусоидальных сигналов заданной амплитуды, но различной частоты, изменяя ее с некоторым шагом. Генерация синусоидального сигнала не представляет собой трудности, поскольку, как замечено, он присущ многим физическим процессам, например, переменному электрическому току или звуковым или световым волнам. Найденная зависимость изменения амплитуды сигнала после прохождения среды для ряда последовательных частот называется амплитудно-частотной характеристикой среды. Построив амплитудно-частотную характеристику среды, можно применить ее к спектральному разложению сигнала, то есть найти, какую амплитуду будет иметь каждая из составляющих нашего периодического сигнала после прохождения среды, а затем сложить все составляющие (гармоники), получив результирующий выходной сигнал. Заметим, что в этом рассуждении не учтено изменение фазы сигнала при его прохождении через среду. Это, естественно, упрощение, которое допустимо, если фазы различных гармоник изменяются одинаково, что часто бывает на практике. Если же это не так, то изменение фаз нужно принимать во внимание и знать фазо-частотную характеристику среды для анализа искажений сигнала. На практике в качестве характеристики линии связи чаще используется не зависимость амплитуды от частоты, а зависимость мощности сигнала от частоты. Обе зависимости дают одну и ту же качественную картину, так как мощность синусоидального сигнала пропорциональна квадрату его амплитуды, но существующие спектральные анализаторы более приспособлены измерять не амплитуду сигнала, а его мощность. Уменьшение мощности сигнала на пути от источника к приемнику кажется интуитивно понятным. Если обратиться к интересующим нас типам сигналов – прямоугольным импульсам, то эффект затухания (упрощенно, без учета других искажений) выражается в уменьшении амплитуды импульсов (рис. 6.9). 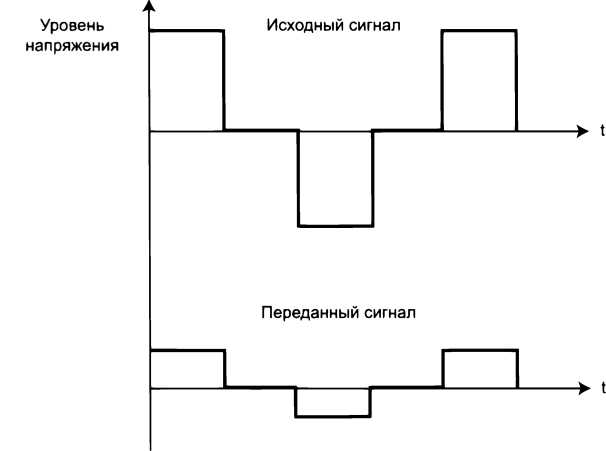 Затухание показывает, насколько уменьшается мощность эталонного синусоидального сигнала на выходе линии связи по отношению к мощности сигнала на входе этой линии. Затухание (А) обычно измеряется в децибелах (дБ) и вычисляется по следующей формуле: 4 = ioigPout/Pm Здесь Pout - мощность сигнала на выходе линии, Р.п – мощность сигнала на входе линии, измеряемые в ваттах. Знание затухания линии очень важно – оно позволяет оценить необходимую мощность передатчика и чувствительность приемника (то есть минимальную мощность сигнала, которую приемник устойчиво распознает). Затухание зависит от длины линии связи, поэтому в качестве характеристики линии связи используется так называемое погонное затухание, то есть затухание на линии связи определенной длины. Для кабелей локальных сетей в качестве такой длины обычно используют 100 м – это значение является максимальной длиной кабеля для многих технологий LAN. Для территориальных линий связи погонное затухание измеряют для расстояния в 1 км. Обычно затуханием характеризуют пассивные участки линии связи, состоящие из кабелей и кроссовых секций, без усилителей и регенераторов. Так как мощность выходного сигнала кабеля без промежуточных усилителей меньше, чем мощность входного, затухание кабеля всегда является отрицательной величиной. Чаще всего при описании параметров линии связи приводятся значения затухания всего для нескольких значений частот. Это объясняется, с одной стороны, стремлением упростить измерения при проверке качества линии. С другой стороны, на практике часто заранее известна основная частота передаваемого сигнала, то есть та частота, гармоника которой имеет наибольшую амплитуду и мощность. Поэтому достаточно знать затухание на этой частоте, чтобы приблизительно оценить искажения передаваемых по линии сигналов. ВНИМАНИЕ Как уже отмечалось, затухание всегда имеет отрицательное значение, однако знак минус часто опускают, из-за чего иногда возникает путаница. Совершенно корректно утверждение, что качество линии связи тем выше, чем больше (с учетом знака) затухание. Если же игнорировать знак, то есть иметь в виду абсолютное значение затухания, то у более качественной линии затухание меньше, и это наиболее распространенная форма интерпретации этого термина. На рис. 6.10 показаны типовые зависимости затухания от частоты для кабелей длиной 100 м на неэкранированной витой паре категорий 5 и 6. Чем выше категория кабеля, тем он качественнее, что отражают графики затухания. Так, кабель категории 5 имеет на частоте 100 МГц затухание -23,6 дБ, а у более качественного кабеля категории 6 на этой же частоте затухание равно -20,6 дБ. Из графиков также видно, что с повышением частоты сигнала затухание увеличивается. Отсюда проистекают проблемы передачи дискретных данных с высокой скоростью: как мы увидим далее, при возрастании скорости передачи сигнала его частота увеличивается, что приводит к росту затухания. Оптический кабель имеет существенно меньшие (по абсолютной величине) величины затухания, обычно в диапазоне от -0,2 до -3 дБ при длине кабеля в 1000 м, а значит, является более качественным, чем кабель на витой паре. Практически для всех оптических волокон типична сложная зависимость затухания от длины волны, которая имеет три так называемых окна прозрачности. На рис. 6.11 показана характерная зависимость затухания для оптического волокна (в оптике принято игнорировать знак затухания, поэтому ось величины затухания идет вверх). Из рисунка видно, что область эффективного использования современных волокон ограничена волнами длин 850 нм, 1310 нм и 1550 нм, каждое окно шириной примерно 100 нм (соответственно частотами 35 ТГц, 23 ТГц и 19,4 ТГц). Окно 1550 нм обеспечивает наименьшие потери, а значит, максимальную дальность при фиксированной мощности передатчика и фиксированной чувствительности приемника.  Рис. 6.10. Затухание неэкранированного кабеля на витой паре  Длина волны источника света, нм Рис. 6.11. Окна прозрачности оптического волокна В качестве характеристики мощности сигнала используются абсолютный и относительный уровни мощности. Абсолютная мощность измеряется в ваттах, относительная мощность – в децибелах. Мощность сигнала рассчитывается по той же формуле, что и затухание. Такая величина, как относительная мощность, используется при сравнении двух сигналов, например, сигнала помехи и информационного сигнала. Затухание также является примером относительной мощности – в этом случае мы сравниваем мощность сигнала на выходе и входе линии связи. Частным случаем относительной мощности является опорная мощность. При расчете опорной мощности уровень, на который делится измеряемая мощность, принимается равным 1 мВт, что и отражается в названии этой единицы мощности, децибел-милливатт, дБм. Опорная мощность р вычисляется по формуле р = 10 1g Р/(1 мВт) [дБм] Здесь Р – абсолютная мощность сигнала в милливаттах. Несмотря на использование отношения в определении опорной мощности, эта единица измерения является абсолютной, а не относительной, так как однозначно преобразует абсолютную мощность сигнала в ваттах в некоторое значение, которое никак не зависит от значения мощности другого сигнала, как это имеет место при определении децибела. Так, нетрудно вычислить соответствие некоторых значений мощности сигнала, выраженных в ваттах и дБм: 1 мВ = 0 дБм, 10 мВ = 10 дБм, 1 В = 30 дБм, 100 кВ = 80 дБм. Опорные значения мощности удобно использовать при расчетах энергетического бюджета линий связи. Пример Пусть требуется определить минимальную опорную мощность х (дБм) передатчика, достаточную для того, чтобы на выходе линии опорная мощность сигнала была не ниже некоторого порогового значения у (дБм). Затухание линии известно и равно А. Пусть X и Y– это абсолютные значения мощности сигнала, заданные в милливаттах на входе и выходе линии соответственно. По определению А = 10 IgA/У Используя свойства логарифмов, приходим к следующему: А = 101gA/y= 101g(A/l)/(y/l) = 101gA/l мВт - 10 lg У/1 мВт. Заметим, два последних члена уравнения по определению являются опорными значениями мощности сигналов на выходе и входе, поэтому приходим к простому соотношению А = х – у, где* - опорная мощность входного сигнала, аг/ – опорная мощность выходного сигнала. Из последнего соотношения следует, что минимальная требуемая мощность передатчика может быть определена как сумма затухания и опорной мощности сигнала на выходе: х = А + у. Величина опорной мощности у выходного сигнала, являющаяся минимальной опорной мощностью сигнала на входе приемника, при котором он еще способен корректно распознавать дискретную информацию, содержащуюся в сигнале, называется порогом чувствительности приемника. Очевидно, что для нормальной работы линии связи минимальная опорная мощность сигнала передатчика, даже ослабленная затуханием линии связи, должна превосходить порог чувствительности приемника: х - А > у. Проверка этого условия и является сутью расчета энергетического бюджета линии. Полоса пропускания На форму сигнала, передаваемого по линии связи, влияет ограниченность ее полосы пропускания. Полоса пропускания (bandwidth) – это непрерывный диапазон частот, для которого затухание не превышает некоторый заранее заданный предел. То есть полоса пропускания определяет диапазон частот синусоидального сигнала, при которых этот сигнал передается по линии связи без значительных искажений. Полоса пропускания измеряется в герцах (Гц). |