Образцы заданий по ТВиМС (2). Книга по математике, составляет для первой полки 0,6 для второй 0,75 для третьей 0,4 для четвертой 0 Найти вероятность того, что взятая наугад книга с наудачу взятой полки есть книга по математике
 Скачать 450 Kb. Скачать 450 Kb.
|
На прилавке 10 различных книг. Причем пять книг стоят по 100 рублей, три книги по 150 рублей и две книги по 200 рублей. Покупатель наудачу выбрал две книги. Найти вероятность того. что их суммарная стоимость 300 рублейВероятность, что студент сдаст первый экзамен, равна 0,9, второй – 0,7, третий – 0,6. Вычислить вероятность того, что студент сдаст не менее двух экзаменов. Два охотника одновременно стреляют в цель. Вероятность попадания у первого охотника равна 0,2, а у второго – 0,6. В результате залпа оказалось одно попадание в цель. Чему равна вероятность того, что промахнулся первый охотник? Приняв вероятность рождения мальчика равной 0,515, найти вероятность того, что среди 10 новорожденных будет 4 девочки. На лекции присутствует 200 человек. Какова вероятность того, что 1 мая родились, по крайней мере, 2 студента? Для проверки качества случайным образом отбираются 3 изделия. Известно, что 2% изделий некондиционные. Случайная величина (СВ) Х – число бракованных изделий в выборке. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 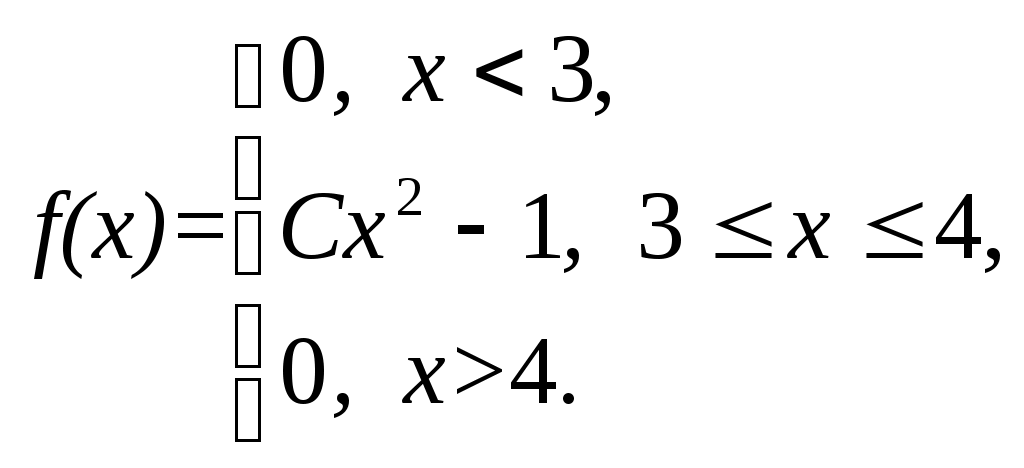 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [1,5; 3,5]. Построить графики функций F(x) и 9. По выборке одномерной случайной величины построить график эмпирической функции распределения построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе найти эмпирическое уравнение Корреляционная таблица:
Вариант № 7 Наудачу взятый телефонный номер состоит из 5 цифр. Как велика вероятность, что в нем все цифры четные? В телестудии находятся три телевизионные камеры. Вероятность того, что в данный момент камера включена соответственно, равна 0,9; 0,8; 0,7. Найти вероятность того, что в данный момент включено не более одной камеры. Вероятности попадания в цель при каждом выстреле для трех стрелков соответственно равны: 0,2; 0,4; 0,6. После одновременного выстрела всех трех стрелков в мишени обнаружено одно попадание. Найти вероятность того, что в цель попал первый стрелок. Вероятность сдачи студентом каждого из 4 экзаменов равна 0,8. Какова вероятность сдачи 3 экзаменов? В страховом обществе застраховано 8000 автолюбителей. Размер страхового взноса равен 6 у.е., а в случае аварии страховое общество выплачивает 500 у.е. Какова вероятность что страховое общество к концу года получит доход превышающий 8000 у.е., если вероятность автолюбителю попасть в аварию равна 0,005? Производится три выстрела по мишени. Вероятность поражения первым выстрелом равна 0,3, вторым – 0,5, третьим – 0,7. Случайная величина (СВ) Х – число поражений мишени. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 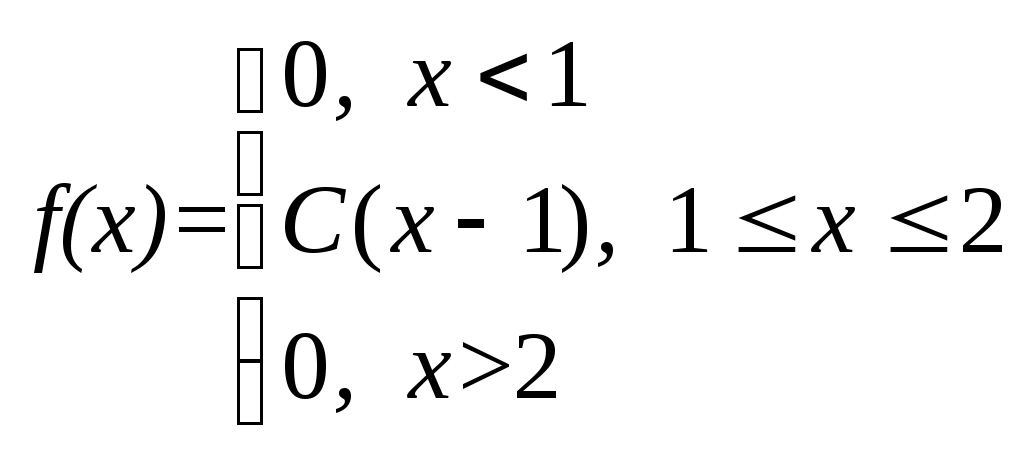 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [1; 1,5]. Построить графики функций F(x) и 9. По выборке одномерной случайной величины построить график эмпирической функции распределения построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе найти эмпирическое уравнение Корреляционная таблица:
Вариант № 8 Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года. Вероятность, что студент сдаст первый экзамен, равна 0.8, второй – 0.7, третий – 0.6. Вычислить вероятность того, что студент сдаст более двух экзаменов. В 3 урнах находятся белые и черные шары. В первой 2 белых и 3черных, во второй 2 белых и 2 черных, в третьей 3 белых и 1 черный. Из первой урны переложили шар во вторую. После этого шар из второй урны переложили в третью. Наконец из третьей урны шар переложили в первую. Чему равна вероятность того, что состав шаров во всех урнах не изменится? Игральная кость брошена 12 раз. Найти вероятность выпадения шестерки 5 раз. В страховом обществе застраховано 11000 автолюбителей. Размер страхового взноса равен 10 у.е., а в случае аварии страховое общество выплачивает 1000 у.е. Какова вероятность что страховое общество к концу года разорится, если вероятность автолюбителю попасть в аварию равна 0,006? Вероятность поражения цели при одном выстреле равна 0.5. Случайная величина (СВ) Х – число поражений цели при трех выстрелах. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 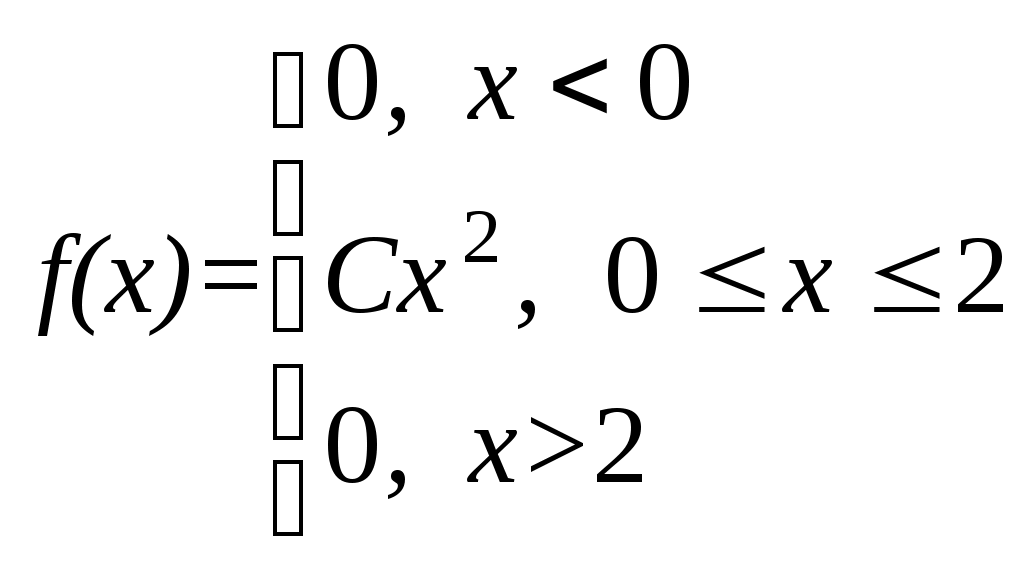 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [0, 1]. Построить графики функций F(x) и 9. По выборке одномерной случайной величины построить график эмпирической функции распределения построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе найти эмпирическое уравнение Корреляционная таблица:
Вариант № 9 |



