Образцы заданий по ТВиМС (2). Книга по математике, составляет для первой полки 0,6 для второй 0,75 для третьей 0,4 для четвертой 0 Найти вероятность того, что взятая наугад книга с наудачу взятой полки есть книга по математике
 Скачать 450 Kb.
|
|
Образцы заданий для контрольной работы по теории вероятностей и математической статистике Для получения допуска к экзамену по предмету «Теория вероятностей и математическая статистика» во время сессии вам будет предложена аудиторная контрольная работа, задания в которой аналогичны примерам, размещенным ниже. Вариант 0 Ребенок играет с четырьмя буквами разрезанной азбуки А, А, М, М. Какова вероятность того, что при случайном разложении букв в ряд он получит слово "МАМА"? Стрелок трижды стреляет в цель. Вероятность попадания при первом выстреле равна 0,5; при втором – 0,6; при третьем – 0,8. Найти вероятность того, что в мишени будет хотя бы одна пробоина. В книжном шкафу имеются книги по математике и психологии. На первой полке стоит 20 томов, на второй полке – 24, на третьей – 30, на четвертой – 28. Вероятность того, что взятая наугад книга по математике, составляет: для первой полки – 0,6; для второй – 0,75:для третьей – 0,4; для четвертой – 0,8. Найти вероятность того, что взятая наугад книга с наудачу взятой полки есть книга по математике. Вероятность того, что автомобиль, взятый напрокат, будет возвращена исправным, равна 0,8. Какова вероятность, что из 4 возвращенных автомобилей 3 окажутся исправными? В страховом обществе застраховано 5000 автолюбителей. В случае аварии страховое общество выплачивает 750 у.е. Какую минимальную стоимость страхового взноса следует установить, чтобы вероятность того, что страховое общество к концу года окажется в убытке, была не больше 0, 0062, если вероятность автолюбителю попасть в аварию равна 0, 004? Симметричную монету бросили два раза. Случайная величина (СВ) Х –– число выпавших гербов. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 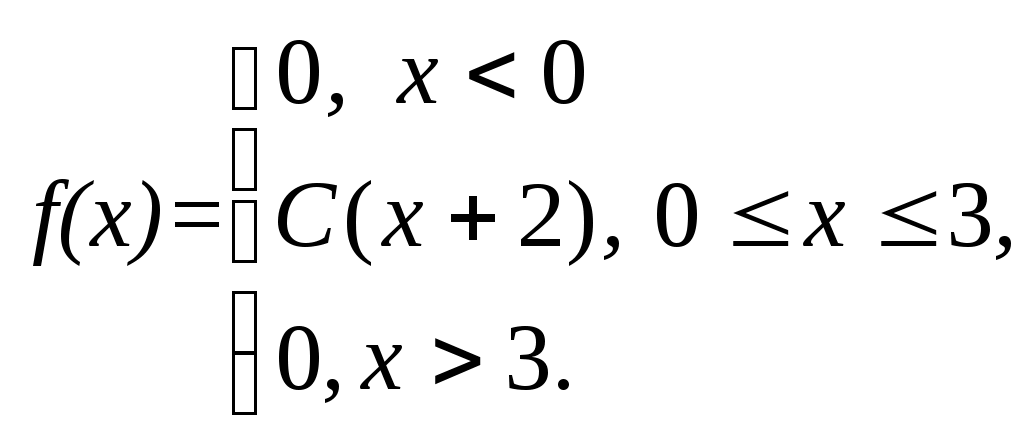 Найти постоянную С, функцию распределения F(x), математическое ожидание и вероятность попадания СВ на отрезок  . Построить графики функций F(x) и  9. По выборке одномерной случайной величины построить график эмпирической функции распределения  ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности  ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости  .Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции  ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе  при уровне значимости ,найти эмпирическое уравнение  прямой лини регрессии  на  .Корреляционная таблица:
Вариант 1 В кондитерской 7 видов пирожных, имеющих одинаковую цену. Выбит чек на 4 пирожные. Найти вероятность, что купленные пирожные одного вида. Вероятность, что студент сдаст первый экзамен, равна 0,8, второй – 0,6, третий – 0,5. Вычислить вероятность того, что студент сдаст не более двух экзаменов. Микросхемы изготавливаются на 3 заводах. Первый производит 45 % общего количества микросхем, второй – 40, третий – 15. Продукция первого завода содержит 70 % стандартных микросхем, второго – 80, третьего – 90. В магазины поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине микросхема окажется стандартной? Вероятность выигрыша по облигации займа за все время его действия равна 0.25. Какова вероятность того, что некто, приобретя 8 облигаций, выиграет по 6 из них? Аппаратура содержит 5000 элементов, каждый из которых независимо от остальных выходит из строя за время Т с вероятностью 0,001. Найти вероятность того, что за время Т откажет не менее двух элементов. Производится три выстрела по мишени. Вероятность поражения первым выстрелом равна 0,4, вторым – 0,5, третьим – 0,8. Случайная величина (СВ) Х – число поражений мишени. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x), построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 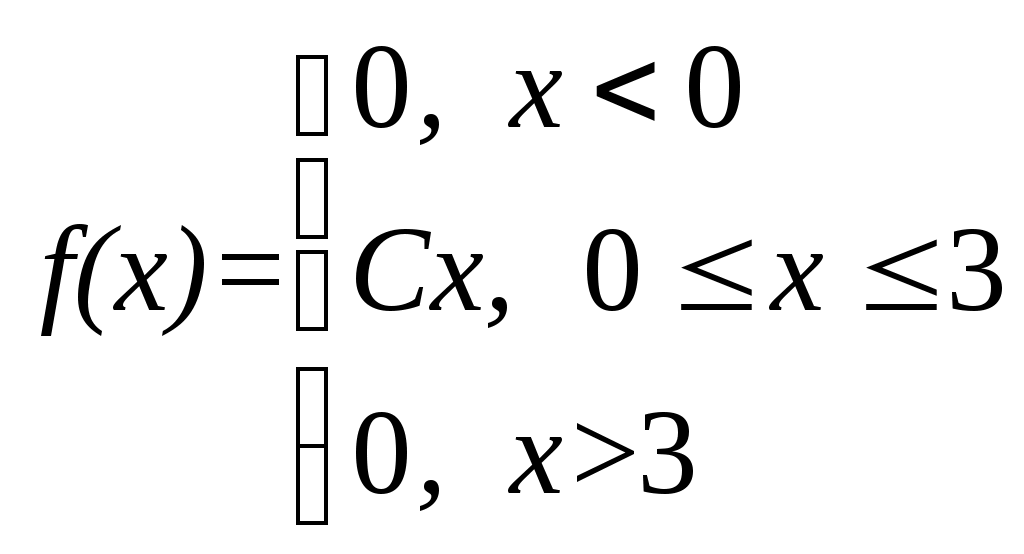 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [0, 1]. Построить графики функций F(x) и 9. По выборке одномерной случайной величины построить график эмпирической функции распределения ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе при уровне значимости ,найти эмпирическое уравнение прямой лини регрессии на .Корреляционная таблица:
Вариант № 2 Наудачу взятый телефонный номер состоит из 5 цифр. Как велика вероятность, что в нем все цифры различные? В урне 4 белых и 3 черных шара. Из урны подряд вынимают два шара. Какова вероятность, что шары разного цвета? На сборку попадают детали трех автоматов. Известно, что первый автомат дает 0.3 % брака, второй – 0,2, и третий – 0.4. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго 2000 и с третьего 2500 деталей. Из последовательности чисел 1,2,...,99,100 выбирают наугад с возвращением 10 чисел. Чему равна вероятность того, что среди них кратных 7 будет не менее двух? Вероятность наступления успеха в каждом испытании равна 0,2. Какова вероятность, что в 600 испытаниях успех наступит ровно 100 раз? В партии из 15 телефонных аппаратов 5 неисправных. Случайная величина (СВ) Х – число неисправных аппаратов среди трех случайно отобранных. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 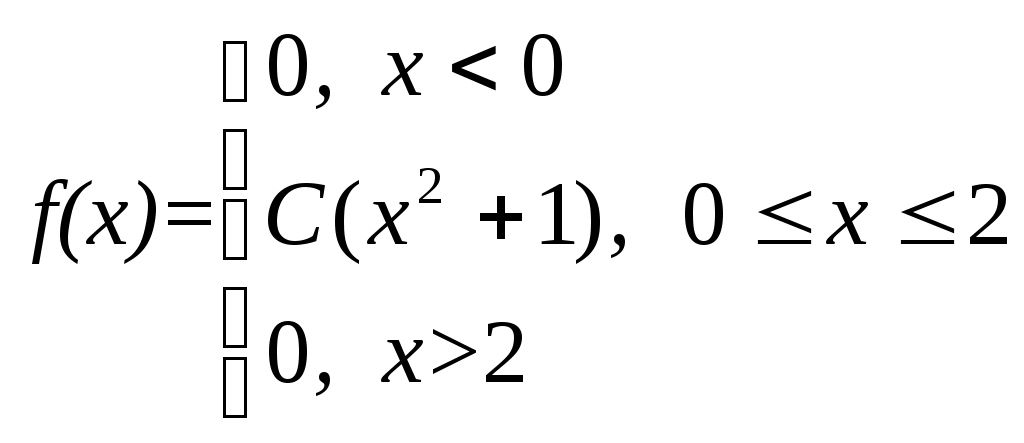 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания на отрезок [0, 1]. Построить графики функций F(x) и  9. По выборке одномерной случайной величины построить график эмпирической функции распределения ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе при уровне значимости ,найти эмпирическое уравнение прямой лини регрессии на .Корреляционная таблица:
Вариант № 3 На полке стоят 15 книг, 5 из них в переплете. Берут наудачу три книги. Какова вероятность того, что все три книги в переплете? Три стрелка стреляют в цель независимо друг от друга. Вероятность попадания в цель для первого стрелка равна 0.6, для второго – 0.7, для третьего – 0.75. Найти вероятность, по крайней мере, одного попадания в цель, если каждый стрелок делает по одному выстрелу. Судоходная компания организует средиземноморские круизы в течение летнего времени и проводит несколько круизов в сезон. Эксперт по туризму, нанятый компанией, предсказывает, что вероятность того, что корабль будет полон в течение сезона, если доллар не подорожает по отношению к рублю равна 0,92, и с вероятностью – 0,7, если доллар подорожает. По оценкам экономистов, вероятность того, что в течение сезона доллар подорожает по отношению к рублю, равна 0,35. Чему равна вероятность того, что билеты на все круизы будут проданы? Применяемый метод лечения приводит к выздоровлению в 90 % случаев. Какова вероятность того, что из 6 больных поправится не менее 5? Игральную кость бросили 120 раз. Найти вероятность того, что шесть очков выпало по крайней мере 25 раз. Вероятность поражения цели при одном выстреле равна 0,6. Случайная величина (СВ) Х – число поражений цели при трех выстрелах. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 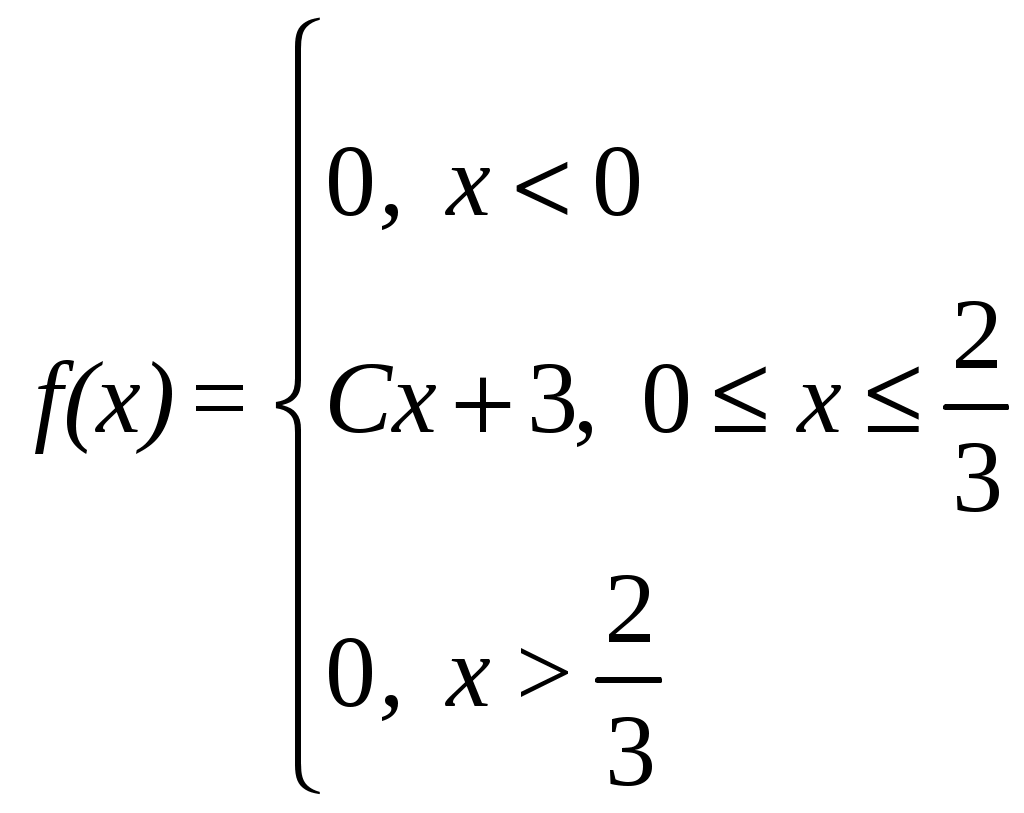 Найти постоянную С, функцию распределения F(x), математическое ожидание и вероятность попадания СВ на отрезок  . Построить графики функций F(x) и .9. По выборке одномерной случайной величины построить график эмпирической функции распределения ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе при уровне значимости ,найти эмпирическое уравнение прямой лини регрессии на .Корреляционная таблица:
Вариант № 4 Собрание, на котором присутствуют 25 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут две женщины и один мужчина. Гардеробщица выдала одновременно номерки четырем лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятность того, что ровно три лица получат свои шляпы. В группе 60 % студентов – юноши. 80 % юношей и 75 % девушек имеют билеты на дискотеку. В группу принесли кем-то потерянный билет. Какова вероятность того, что он принадлежал юноше? Игральная кость брошена 10 раз. Найти вероятность выпадения единицы не менее 2 раз. В страховом обществе застраховано 7000 автолюбителей. Размер страхового взноса равен 8 у.е., а в случае аварии страховое общество выплачивает 800 у.е. Какова вероятность что страховое общество к концу года разорится, если вероятность автолюбителю попасть в аварию равна 0,007? Вероятность сдачи экзамена для каждого из трех студентов равна 0.8. Случайная величина (СВ) Х – число студентов сдавших экзамен. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 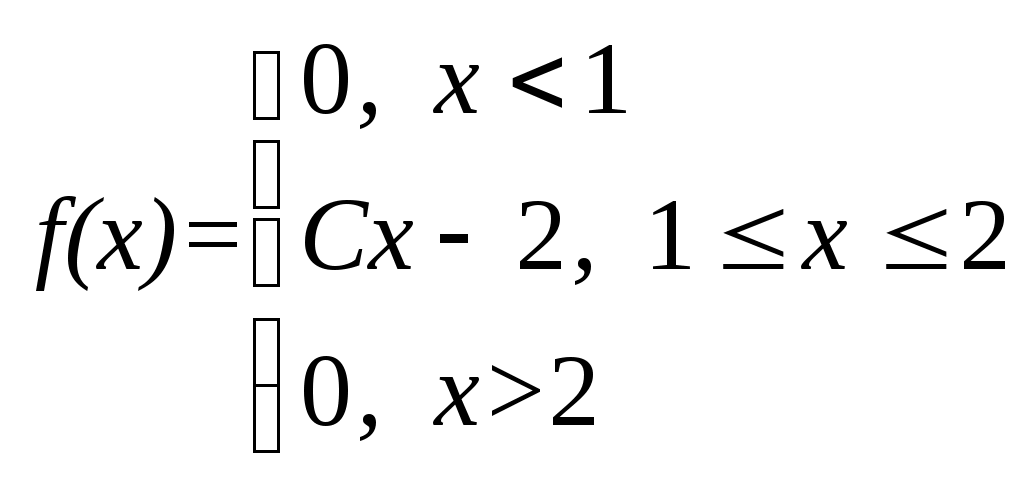 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [0,5; 1,5]. Построить графики функций F(x) и 9. По выборке одномерной случайной величины построить график эмпирической функции распределения ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .Одномерная выборка:
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе при уровне значимости ,найти эмпирическое уравнение прямой лини регрессии на .Корреляционная таблица:
Вариант № 5 В группе спортсменов 7 лыжников и 3 конькобежца. Из группы случайным образом выбраны 3 спортсмена. Найти вероятность того, что все выбранные спортсмены окажутся лыжниками. Брошены две игральные кости. Чему равна вероятность того, что хотя бы на одной из них выпадет 5 очков? Некто, заблудившись в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час? В урне 10 белых и 5 черных шаров. Чему равна вероятность того, что, вынув наудачу с возвращением 14 шаров, получим белых не менее 12? Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Коммутатор обслуживает 500 абонентов. Какова вероятность, что в течение часа позвонят два абонента? Из 10 студентов, среди которых два отличника, случайным образом выбраны два студента. Случайная величина (СВ) Х – число отличников среди выбранных. Получить ряд распределения, вычислить функцию распределения F(x) и построить ее график. Вычислить функцию распределения F(x) и построить ее график. Найти математическое ожидание и дисперсию дискретной случайной величины, заданной рядом распределения
Плотность вероятности случайной величины Х равна 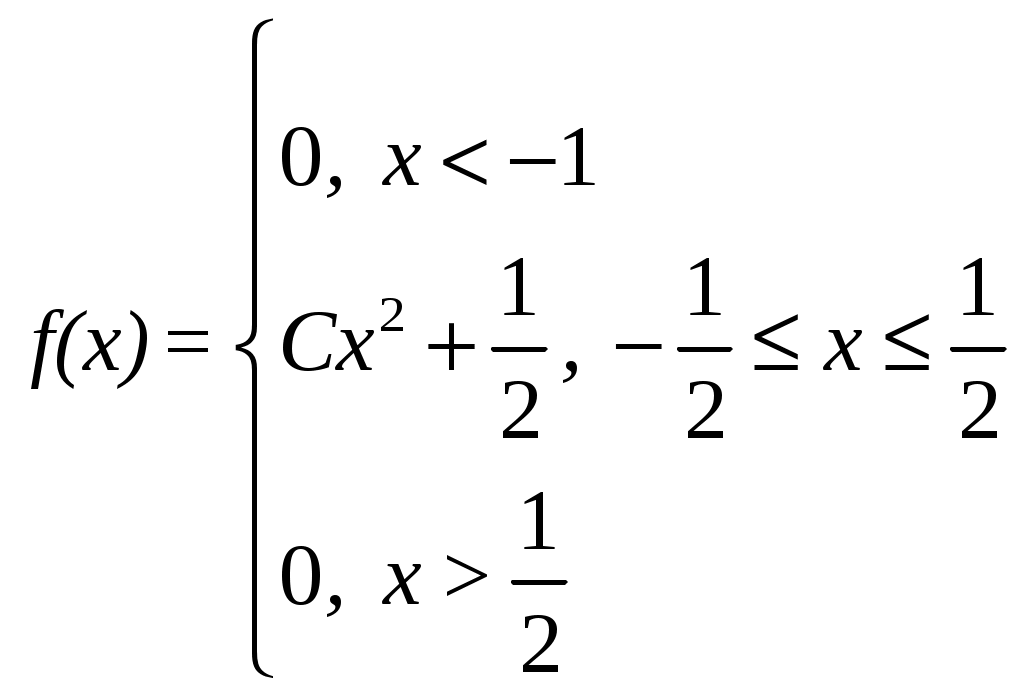 Найти постоянную С, функцию распределения F(x), математическое ожидание, дисперсию и вероятность попадания СВ на отрезок [0; 0,25]. Построить графики функций F(x) и . 9. По выборке одномерной случайной величины построить график эмпирической функции распределения ,построить гистограмму относительных частот равноинтервальным способом, вычислить точечные оценки математического ожидания и дисперсии, вычислить интервальные оценки математического ожидания и дисперсии при доверительной вероятности ,выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия Пирсона при уровне значимости .Одномерная выборка
10. По корреляционной таблице двумерной случайной величины вычислить выборочный коэффициент корреляции ,проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе при уровне значимости ,найти эмпирическое уравнении:е прямой лини регрессии на .Корреляционная таблица:
Вариант № 6 |
