Колебания. Колебания и волны
 Скачать 0.72 Mb.
|
|
Затухающие механические колебания Гармонические колебания - это идеальные колебания, возникающие при наличии только квазиупругих сил. Однако в любой системе присутствуют силы трения, которые приводят к потере энергии, запасенной в осцилляторе и колебания с течением времени затухают. Колебания с убывающей амплитудой называются затухающими. Пусть на точку, кроме квазиупругой силы, действуют также сила трения, пропорциональная скорости   , где r – коэффициент сопротивления (трения). Применив второй закон Ньютона, получим:  или  , ,пусть  =  - собственная циклическая частота,  - коэффициент затухания,тогда дифференциальное уравнение затухающих колебаний примет вид  +2β + ²x = 0.Его решением является уравнение затухающих колебаний x=   сos (ωt + ), видно, что амплитуда колебаний убывает по закону A= ,а циклическая частота равна ω=  .График затухающего колебания представлен на рис. 8. Время релаксации  - это время, за которое амплитуда колебаний уменьшается в eраз.Согласно определению времени релаксации  ,отсюда  ,  , .Таким образом, становится понятен физический смысл коэффициента затухания:  - величина, обратная времени затухания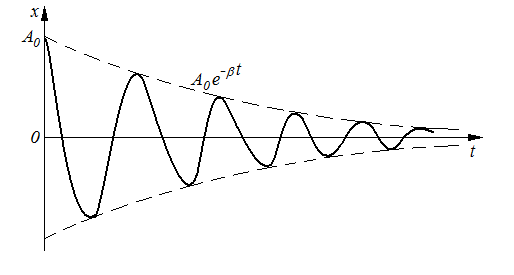. Рис. 8 О степени затухания можно судить также по логарифмическому декременту затухания, равному логарифму отношения двух последующих амплитуд: 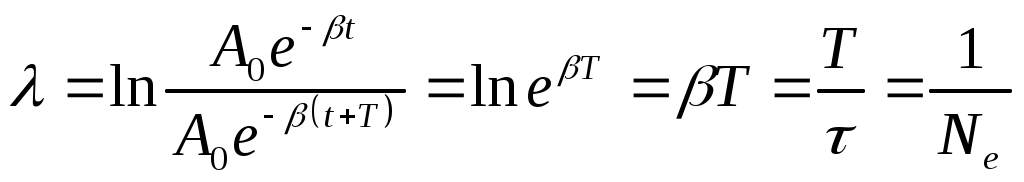 ,здесь  - количество колебаний за время релаксации.Затухающие электрические колебания Затухание электрических колебаний происходит из-за наличия в колебательном контуре электрического сопротивления R. Дифференциальное уравнение затухающих колебаний величины заряда выводится из закона Ома, имеющего в данном случае вид UС+IR =  ,где  - напряжение на конденсаторе,  - ЭДС самоиндукции. С учетом, что сила тока равна ,можно записать  или  .Таким образом, дифференциальное уравнение и его решение имеют вид  + ,  ,где ω0=  - собственная циклическая частота;  , - коэффициент затухания;  - циклическая частота затухающих колебаний.Закон убывания амплитуды 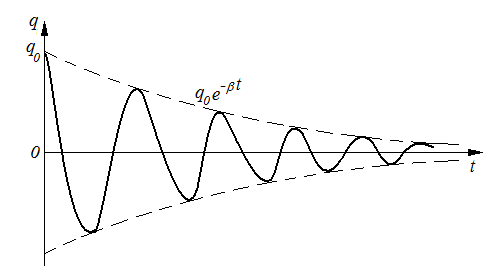 представлен на рис. 9 штриховой линией. Рис. 9 Время релаксации - это время, за которое амплитуда колебаний уменьшается в eраз.Согласно определению времени релаксации  ,отсюда , , .Таким образом, становится понятен физический смысл коэффициента затухания: - величина, обратная времени затухания.О степени затухания можно судить также по логарифмическому декременту затухания, равному логарифму отношения двух последующих амплитуд: 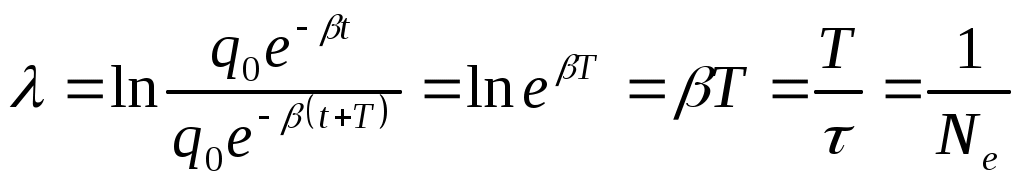 ,здесь - количество колебаний за время релаксации.Можно отметить, что уравнения, описывающие механические и электрические колебания аналогичны друг другу. Вынужденные механические колебания Вынужденные механические колебания происходят под действием периодической вынуждающей силы  ,благодаря которой в систему подводится энергия, и колебания не затухают. Применив второй закон Ньютона, получим: + или  , .Пусть = - собственная циклическая частота, - коэффициент затухания, тогда дифференциальное уравнение вынужденных колебаний примет вид +2β + ²x = Его решением является уравнение вынужденных колебаний (установившиеся колебания) x= сos( t 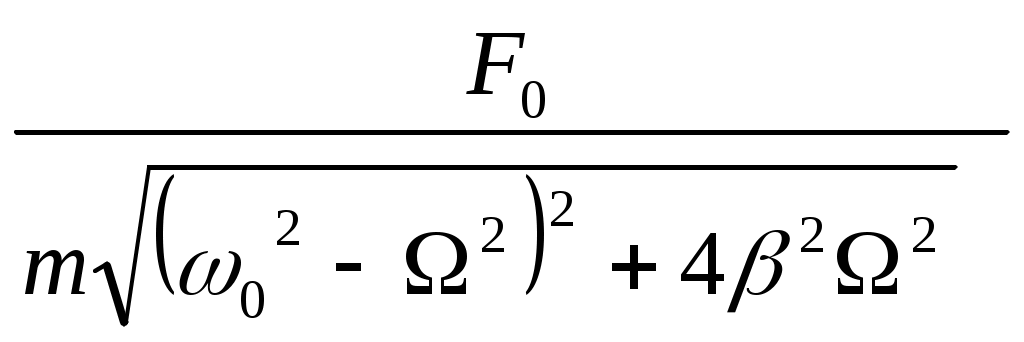+ ), где A=  - амплитуда установившихся колебаний, начальная фаза определяется соотношением .Из уравнения для амплитуды следует, что при частоте  =  амплитуда становится максимальной, т.е. наблюдается резонанс, - резонансная частота.УПРУГИЕ ВОЛНЫ Колебания, возникающие в некоторой точке упругой среды, передаются соседним точкам, которые тоже начинают колебаться. Волной называется процесс распространения колебаний в сплошной среде. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. С волной от частицы к частице передаются колебательные движения и энергия. Основным свойством волны является перенос энергии без переноса вещества. Упругими волнами называются волны, распространяющиеся в упругой среде (твердой, жидкой или газообразной). Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются вдоль направления распространения волны, в поперечных волнах частицы колеблются перпендикулярно направлению распространения волны. Продольная волна возникает в средах, в которых возникают упругие силы деформации сжатия или растяжения. Эта волна распространяется в твердой, в жидкой и в газообразной средах. Поперечная волна может возникнуть в среде, в которой возникают упругие силы при деформации сдвига, а это возможно только в твердых телах. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными, а волновой фронт все время перемещается и является передней волновой поверхностью. Если волновыми поверхностями являются плоскости, перпендикулярные направлению распространения волны, то такие волны называются плоскими. Если волновыми поверхностями являются сферы, то такие волны – сферические. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны  , т.е. длина волны равна расстоянию, на которое распространяется волна за период T ,где  – скорость распространения волны.Период колебаний связан с частотой  соотношением  , тогда  .Уравнения плоской и сферической волны Уравнением волны называется выражение, которое дает смещение  колеблющейся точки, как функцию ее координат x,y,z и времениt  Для определения уравнения волны, нужно предположить, что колебания носят гармонически характер и для упрощения направим ось ОX так чтобы она совпадала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси OX. Смещение точки будет зависеть от x и t  Колебания точек, лежащих в плоскости x=0 имеет вид  За время  волна, имеющая скорость распространения , окажется в координате x относительно плоскости x=0. Колебания частиц, лежащих в плоскости x, будут отставать по времени от колебаний точек в плоскости x=0 на , т.е. имеют вид Уравнения плоской волны запишется  , (1)где  - фаза волны.Величина определяет смещение точек с координатой x в произвольный момент времени t. Уравнение (1) описывают волну, распространяющуюся в положительном направлении оси OX. Волна, распространяющаяся в отрицательном направлении оси OX, описывается уравнением  .Перепишем фазу волны в виде  ,где  - называется волновым числом.Уравнение плоской волны (1) можно переписать с учетом волнового числа  .Уравнение сферической волны имеет вид  , где r – расстояние от центра волны до рассматриваемой точки среды, А – амплитуда колебаний, которая уменьшается с расстоянием по закону  .Если волна распространяется в произвольном направлении, то уравнение будет иметь вид  , (2)где  - радиус вектор, определяющий положение волновой поверхности,  - волновой вектор, который направлен по нормали  к волновой поверхности. Скалярное произведение  можно выразить через проекции векторов на координатные оси  ,где  ,  ,  ,  - это углы между направлением волнового вектора и осями x,y,z.Амплитуда колебаний не изменятся со временем, и энергия волны не поглощается средой. Если фаза волны не изменяется т.е.  Продифференцировав это выражение, получим  , т.е.  - скорость распространения волны это и есть скорость распространения постоянной фазы, поэтому эту скорость называют фазовой скоростью. |