4 вариант. Количество выбрасываемых аэрозольных частиц не должно превышать Н
 Скачать 24.94 Kb. Скачать 24.94 Kb.
|
|
Вариант 4 Тепловая электростанция для генерации электрического тока использует уголь. Агентство по защите окружающей среды установило следующие ограничения: концентрация сернистого газа не должна превышать Ксг, количество выбрасываемых аэрозольных частиц не должно превышать Нач граммов в час. Тепловая электростанция использует пылевидный уголь двух сортов, С1 и С2. Перед сжиганием эти сорта угля обычно смешиваются. Для простоты предполагается, что сернистая составляющая в смеси углей определяется как средневзвешенное от доли угля каждого сорта в смеси. Найти оптимальную смесь углей обоих сортов, обеспечивающую максимальное количество генерируемой энергии в час. Характеристики используемых сортов угля для каждого варианта задания приведены в таблице.
Решение Составляем математическую модель задачи. Поскольку для генерации электрического тока используется только уголь двух видов С1 и С2, то переменными для этой задачи, очевидно, будут 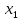 – количество пылевидного сорта угля С1 (в тоннах), используемой для генерации электрического тока; – количество пылевидного сорта угля С1 (в тоннах), используемой для генерации электрического тока;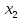 – количество пылевидного сорта угля С2 (в тоннах), используемой для генерации электрического тока. – количество пылевидного сорта угля С2 (в тоннах), используемой для генерации электрического тока.Целевая функция задачи – общая генерируемая мощность (в кВт) тепловой электростанцией в час, и она должна быть максимальной. В данном случае это можно записать следующим образом: максимизировать 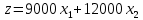 . .Ограничения модели должны отражать требования агентства по защите окружающей среды. Концентрация сернистого газа при сжигании тонны смеси угля в час (Ксг); соответствующее ограничение будет записано следующим образом: 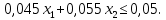 Количество выбрасываемых аэрозольных частиц не должно превышать Нач граммов в час; соответствующее ограничение будет записано следующим образом: 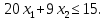 Окончательно модель примет следующий вид: максимизировать 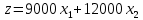 при ограничениях 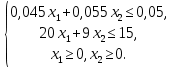 Решаем задачу графическим методом. Для этого заменяем в каждом неравенстве знаки неравенства на равенства и находим 2 точки для построения данной прямой. Рассмотрим каждое ограничение отдельно. 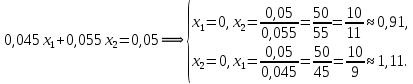 Для построения данной прямой имеем 2 точки: (0; 0,91) и (1,11; 0). 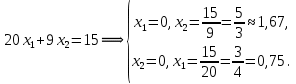 Для построения данной прямой имеем 2 точки: (0; 1,67) и (0; 0,75). Последние ограничения 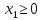 и и 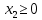 указывают на неотрицательность искомых переменных, и ограничивают область допустимых решений (ОДР) первым квадрантом. указывают на неотрицательность искомых переменных, и ограничивают область допустимых решений (ОДР) первым квадрантом. После построения ОДР добавляем вектор цели. Начало данного вектора в точке (0; 0), конец вектора в (9000; 12000). Поскольку вторую координату в ОДР отметить проблематично, то уменьшаем его прямо пропорционально в 20000 раз. Тогда концом вектора служит другая точка с координатами (0,45; 0,6). Поскольку в данной модели следует максимизировать целевую функцию, поэтому нужно идти в направлении увеличения ее значений. В нашем случае, после изображения вектора цели необходимо его перемещать параллельно до его последнего касания с ОДР. На рисунке показано графическое решение этой задачи. 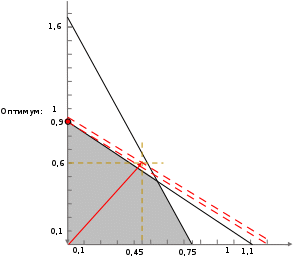 Определяем координаты оптимальной точки и значение целевой функции Видно, что оптимальное решение находится на пересечении двух прямых 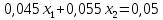 и и 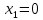 . Зная, что . Зная, что 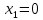 , подставляем его в первое уравнение и имеем, что , подставляем его в первое уравнение и имеем, что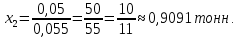 При этих значениях переменных максимальная генерируемая мощность (в кВт) тепловой электростанцией в час составляет 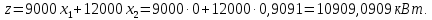 Ответ: максимальная генерируемая мощность составляет 10909,0909 кВт в час при использовании пылевидного сорта угля С2 в количестве 0,9091 тонн, т.е. 909,1 кг. |
