Комбинаторика. Комбинаторика теория. Комбинаторика. Комбинаторные задачи
 Скачать 307.5 Kb.
|
|
Комбинаторика. Комбинаторные задачи. Решим задачу: пример1. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать? Решение.
Всего вариантов столько же, сколько клеток в таблице. По формулировке и способу решения задачи, становится понятно, какой теме будет посвящено наше занятие. Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать». Какой, по вашему мнению, самый эффективный способ решения данной задачи? С использованием какого правила? Правило умножения. Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В , следует перемножить число всех исходов испытания А и число всех исходов испытания В. Пример 2. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг? Решение будем искать с помощью «дерева возможных вариантов». Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя. Пусть теперь верхняя полоса – синего цвета, это вторая «веточка». Тогда средняя полоса может быть белой или красной, а нижняя - соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая. Аналогично рассматривается случай для верхней полосы красного цвета. Получается еще два варианта: красная, белая, синяя и красная, синяя, белая. 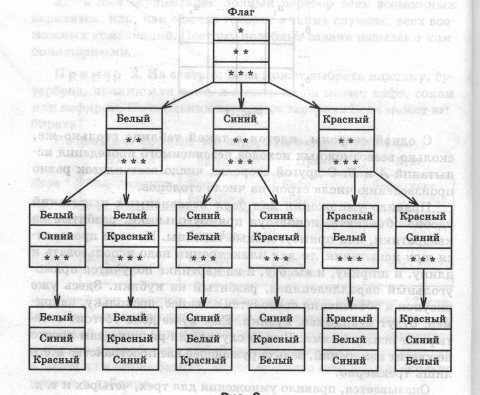 Всего 6 комбинаций. Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов». А вот так выглядит «дерево возможных вариантов» для такого примера 3: Пример 3. Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза? Ответ: 24. 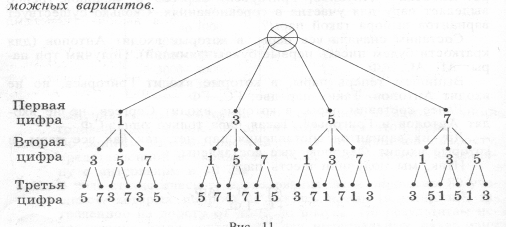 И вновь вопрос: как можно решить задачи такого типа без использования построения дерева? (перестановки).. Рассмотрим пример. Имеются три книги. Обозначим их буквами a ,b и c.Эти книги нужно расставить на полке по-разному: а b с, а с b, b а с, b с а, с а b, с b а. Каждое из этих расположений и называют перестановкой из трех элементов. Перестановкой из n элементов называют каждое расположение этих элементов в определенном порядке. Обозначают: Рn = n! (n факториал). n! =  .Например: 3! =  , 1! = 1.Поэтому задачу с книгами можно решить так: Р3= .Задача №1. Сколькими способами 4 человека могут разместиться на четырехместной скамейке? Решение: Р4 =  Ответ: 24. Задача №2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2, 4.6? Решение: из цифр 0,2.4.6 можно составить Р4 перестановок. Из этого числа нужно исключить те перестановки, которые начинаются с 0. Число таких перестановок Р3. Значит искомое число четырехзначных чисел, которые можно составить из цифр 0,2,4,6 равно: Р4 – Р3= 4!-3!=  Ответ: 18.Задача №3. Имеются 9 различных книг, четыре из которых учебники. Сколькими способами можно расставить книги на полке так, чтобы все учебники стояли рядом? Решение: сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не 9, а 6 книг. Это можно сделать Р6 способами. И в каждой из полученных комбинаций можно выполнить Р4 перестановок учебников. Значит, искомое число способов расположения книг равно произведению: Р6*Р4=  Задача № 4. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно расставить расписание уроков на этот день так, чтобы два урока математики стояли рядом? Решение: Р6  * Р2= Ответ: 1440. Вторым видом комбинаций являются размещения. Пусть имеются 4 шара и 3 пустых ячейки. Обозначим шары буквами a, b, c, d. В пустые ячейки можно по-разному разместить три шара из этого набора.
и т.д. Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещениями из четырех элементов по три и обозначают  А
Из составленной таблицы видно, что таких комбинаций 24. Размещением из n элементов по k (n  k) называется любое множество, состоящее из k элементов, взятых в определенном порядке из данных n элементов и обозначается А .И необязательно каждый раз составлять схемы или таблицы. Достаточно знать формулу: Если размещения составляются из n элементов по n, то А  Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.  Задача 5.Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета. Решение: А  (способов).Задача 6. На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места а) 4 фотографии; б) 6 фотографий. Решение: а) А  б) А  Задача 7. Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0,1,2,3,4,5 и 6? Объяснение: если среди семи цифр нет нуля, то число трехзначных чисел которые можно составить из этих цифр равно числу размещений из 7 элементов по 3 А  . Однако, среди данных семи чисел есть цифра 0, с которой не может начинаться трехзначное число. Поэтому из размещений из 7 элементов по 3 нужно исключить те, у которых первым элементом является цифра 0.Их число равно числу размещений из 6 элементов по 2.Значит, искомое число равно: А  .Решение: А  Задача 8. Из трехзначных чисел, записанных с помощью цифр 1,2,3,4,5,6,7,8,9 (без повторения цифр), сколько таких, в которых: а) не встречаются цифры 6 и 7; б) цифра 8 является последней? Решение: а) А  б) А  Задача 9. Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от 0? Решение: А  А теперь рассмотрим такой сюжет: Имеется 5 гвоздик разного цвета. Обозначим их буквами a, b, c, d, e. Требуется составить букет из трех гвоздик. Выясним, какие букеты можно составить. Если в букет входит гвоздика a, то можно составить такие букеты: abc, abd, abc, acd, ace, adc. Если в букет не входит гвоздика a, а входит гвоздика b, то можно получить такие букеты: bcd, bce, bdc. Наконец, если в букет не входит ни гвоздика a,гвоздика b, то можно составить букет cde. Мы показали все возможные способы составления букетов, в которых по-разному сочетаются три гвоздики из данных пяти. Говорят, что составлены всевозможные сочетания из 5-ти элементов по 3. Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов и обозначается С в отличие от размещений, в сочетаниях не имеет значения, в каком порядке указаны элементы. С  Поэтому пример про гвоздики можно быстро решить так: Решение: С  Задача 10. Из 15 человек туристической группы надо выбрать трех дежурных. Сколькими способами это можно сделать? Решение: С  Задача 11. Из вазы с фруктами, где лежат 9 яблок и 6 груш, нужно выбрать 3 яблока и 2 груши. Сколькими способами можно это сделать? Решение: 3 яблока из 9-ти можно выбрать С  способами. При каждом выборе яблок груши можно выбрать С способами. Поэтому по правилу умножения выбор фруктов можно сделать С  способами.Решение: С = |