потери. Потери. Компенсация мощность электроснабжение измерительный
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Глава 2. Источники реактивной мощности 2.1 Анализ систем управления конденсаторными установками компенсации реактивной мощности в сети 0,4 кВ В системе электроснабжения промышленных предприятий большее применение нашли установки компенсации реактивной мощности с помощью батарей статических конденсаторов, которые предназначены для компенсации индуктивной компоненты и коррекции коэффициента мощности. В связи с тем, что количество электроэнергии, потребляемой предприятием, изменяется в течение суток, изменяется и потребность в реактивной мощности. В первой главе выполнен анализ существующих установок компенсации реактивной мощности, все они работают по принципу, который основан на измерении угла сдвига фаз между током и напряжением. Типовая принципиальная электрическая схема низковольтной КУ с автоматическим регулированием мощности конденсаторных батарей представлена на рис. 2.1. Структурная схема устройства компенсации реактивной мощности представлена на рис. 2.2. 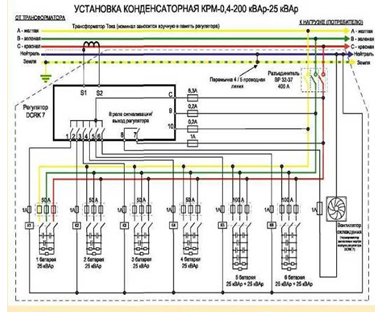 Рис. 2.1 – Принципиальная электрическая схема конденсаторной установки КРМ-0,4-200 кВар 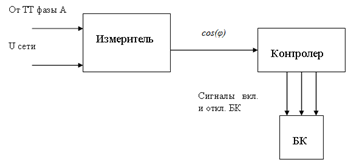 Рис. 2.2 – Структурная схема устройства управления конденсаторной установкой                                           Сигнал на отключение N-ой секции конденсаторных батарей 1 9 6 8 7 5 4 3 2 нет нет да да Блок управления конденсаторными батареями Сигнал на включение N-ой секции конденсаторных батарей КОНЕЦ cos φ > - 0,9 cos φ <0..0,9 Расчет коэффициента мощности фазыcos φА uA=UmA·sin(ωt+ψuA) iA=ImA·sin(ωt+ψiA) НАЧАЛО Рис. 2.3 – Блок-схема алгоритма работы УКРМ 2.2 Формирование вектора напряжения на шинах узла нагруки Задача формирования вектора напряжения на шинах СК имеет ряд приближенных решений. К ним относятся: – определение напряжения на шинах КС через падение напряжения на активном сопротивлении нагрузки; – метод неполного дифференцирования, где пренебрегают трансформаторной ЭДС и ЭДС вращения в уравнении статора СК. Анализ данных методов с целью возможности их применения при формировании вектора напряжения на шинах СК показал отсутствие желаемой универсальности. Для устранения данного недостатка предлагается формировать вектор напряжения на шинах СК с помощью метода двух узлов. Под методом двух узлов понимается метод расчета электрических цепей, в которых за искомое принимают напряжение между двумя узлами схемы с последующим определением токов в ветвях цепи [28]. Всегда можно выделить ветвь компенсации реактивной мощности, эквивалентную пассивную и эквивалентную асинхронную нагрузки. Ветвь компенсации реактивной мощности, реализуемой СК, представлена источником внутренней ЭДС Еi с внутренним сопротивлением Z = rS + jXS, где Еi рассчитывается с помощью уравнений Парка-Горева в модификации Л.П. Веретенникова с учетом переходных процессов в статоре СК. Эквивалентная пассивная нагрузка 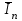 характеризует статическую активно-индуктивную нагрузку. характеризует статическую активно-индуктивную нагрузку.Эквивалентная асинхронная нагрузка 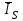 характеризуется асинхронным двигателем, который представлен уравнениями Парка-Горева и включен на шины с напряжением U. характеризуется асинхронным двигателем, который представлен уравнениями Парка-Горева и включен на шины с напряжением U.Для моделирования узла нагрузки требуется единая система координат, в которой были бы записаны дифференциальные уравнения СК и нагрузки в узле. Выбор скорости вращения единой системы координат k может быть следующий. Если k = 0 и система координат сцеплена с вращающимся магнитным полем, то ее называют синхронно вращающейся системой координат с обозначениями осей X, Y, 0. При k = 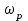 система координат сцеплена с ротором СК, которую целесообразно применить из-за магнитной асимметрии ротора СК. Учитывая, что ротор СК вращается синхронно с полем, в дальнейшем систему координат будем называть системой координат ротора или система координат сцеплена с ротором СК, которую целесообразно применить из-за магнитной асимметрии ротора СК. Учитывая, что ротор СК вращается синхронно с полем, в дальнейшем систему координат будем называть системой координат ротора или 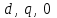 . Таким образом, окончательно принимаем синхронно вращающуюся систему ротора . Таким образом, окончательно принимаем синхронно вращающуюся систему ротора 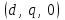  или X, Y, 0. или X, Y, 0. При исследовании электромагнитных переходных процессов СК принято[28]: 1. Система координат, в которой записаны дифференциальные уравнения СК, жестко связана с вращающейся системой координат ротора (полем). Положительное вращение осей системы координат против часовой стрелки. Ось q определяет ось d. Вектор напряжения на шинах расположен в первом квадрате системы координат. Переходные процессы в машинах переменного тока рассматриваются с помощью уравнений Парка–Горева в модификации Л.П. Веретенникова. Пассивная нагрузка линейна. Активные и индуктивные сопротивления соединительных линий равны нулю или вынесены в соответствующие параметры элементов СК. Пассивная нагрузка по фазам распределяется симметрично. Рассмотрим схему замещения статора СК, которая приведена на рисунке 2.4. Запишем уравнения статора СК согласно второму закону Кирхгофа в ортогональной системе координат. 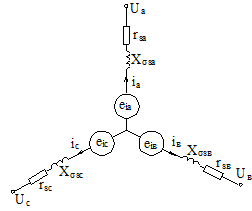 Рис. 2.4 – Схема замещения СК 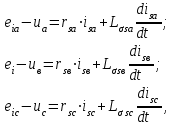 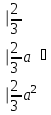 (2.1) (2.1)где 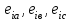 – величины мгновенных значений внутренней ЭДС фаз a, в, c СК; – величины мгновенных значений внутренней ЭДС фаз a, в, c СК;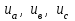 – величины мгновенных значений напряжений фаз a, в, c СК; – величины мгновенных значений напряжений фаз a, в, c СК;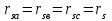 – активные сопротивления фаз статора СК; – активные сопротивления фаз статора СК;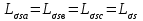 – индуктивности рассеяния фаз статора СК; – индуктивности рассеяния фаз статора СК;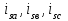 – величины мгновенных значений токов статора фаз a, в, c. СК. – величины мгновенных значений токов статора фаз a, в, c. СК.Сложив уравнения (3.61), запишем уравнение статора в векторной форме в неподвижной системе координат 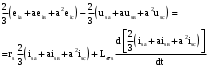 , (2.2) , (2.2) где 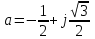 . .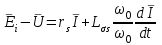 Или 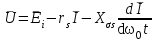 . (2.3) . (2.3)Из уравнения (2.3) можно записать проекции вектора напряжения статора на оси 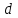 и и 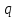 : : 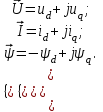 (2.4) (2.4)С учетом (2.4) запишем в проекциях на оси d и q уравнения статора СК в синхронном времени: 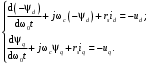 (2.5) (2.5)Из векторной диаграммы СК, показанной на рисунке 2.5, выразим проекции вектора напряжения на шинах нагрузки на оси d и q: 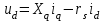 , (2.6) , (2.6)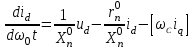 (2.7) (2.7)Умножив уравнение (2.7) на j и сложив его с уравнением (2.6), получим: 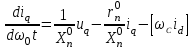 (2.8) (2.8)Преобразуем (2.8): 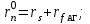 Или 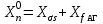 (2.9) (2.9)Вектор внутренней ЭДС 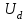 имеет свою особенность. Учитывая математическую связь имеет свою особенность. Учитывая математическую связь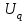 (2.10) (2.10)и принятое положение вектора потокосцепления на комплексной плоскости (см. рис. 2.5) 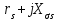 , вектор внутренней ЭДС можно записать в виде , вектор внутренней ЭДС можно записать в виде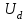 . (2.11) . (2.11)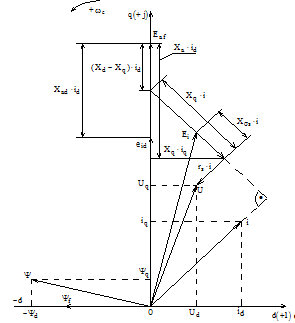 Рис. 2.5. – Векторная диаграмма СК Численное значение проекции 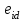 , отстающей на 0,5 , отстающей на 0,5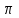 от проекции от проекции 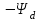 , определяем из выражения , определяем из выражения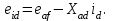 (2.12) (2.12)Численное значение проекции 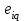 , отстающей на 0,5 , отстающей на 0,5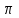 от проекции от проекции 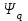 , определяется по формуле , определяется по формуле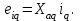 (2.13) (2.13)Из векторной диаграммы (рис. 2.5) запишем численные значения проекций вектора 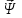 на оси d и q: на оси d и q: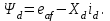 (2.14) (2.14)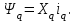 (2.15) (2.15)Вычтем из (2.12) выражение (2.14) и получим проекцию вектора тока статора СК на ось d: 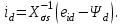 (2.16) (2.16)Аналогично вычтем из (2.13) выражение (2.15) и получим проекцию вектора тока статора СК на ось q: 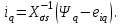 (2.17) (2.17)Выразим из (2.9) с учетом (2.12) и (2.13) проекции вектора напряжения на статоре СК: 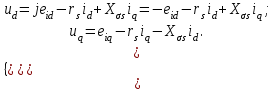 (2.18) (2.18)Подставив (2.17) в (2.5), получим дифференциальные уравнения статора СК через проекцию векторов внутренней ЭДС, потокосцеплений и токов статора в синхронном времени, которые приведены к относительному виду с помощью системы относительных единиц статора: 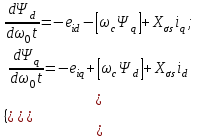 (2.19) (2.19)Подставив (2.16) и (2.17) в (2.19), получим уравнения статора, исключив ток: 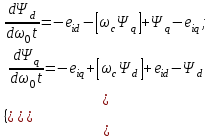 (2.20) (2.20)Выразим модуль напряжения статора СК 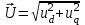 Запишем на основании второго закона Кирхгофа дифференциальные уравнения ротора СК в проекциях на оси d и q в синхронном времени, которые приведены к относительному виду с помощью системы относительных единиц ротора: 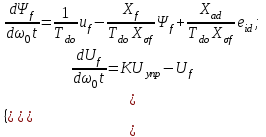 (2.21) (2.21)где 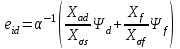 ; ;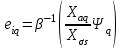 ; ;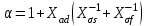 ; ;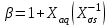 . .Для практического применения при моделировании СК отметим следующие моменты: – вектор напряжения на узле нагрузки, определенный по методу двух узлов, располагается в первом квадранте под углом 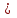 45; 45; – все участники нагрузки должны приводиться к собственным базисам. Для этого необходимо физические величины (напряжение, ток) умножить на собственный базис и разделить на базис СК. Формирование вектора напряжения на шинах узла нагрузки использовано при математическом описании имитационной модели СК (Приложение Б), работающей на активно-индуктивную и асинхронную нагрузки. 2.3 Нечеткое управление синхронного компенсатора с применением алгоритма Мамдани Рассмотрим нечеткое управление синхронного компенсатора с применением алгоритма Мамдани. Источники реактивной мощности (ИРМ) предназначены для реализации баланса реактивной мощности в электроэнергетической системе. Они обеспечивают генерирование и потребление реактивной мощности. Основными параметрами регулирования ИРМ является напряжение в точке его подключения и \ или реактивная мощность нагрузки, для компенсации которой он предназначен, отдельно или вместе. ИРМ решает следующие задачи: снижение потерь активной мощности в сети; регулирование напряжения и ограничение напряжения в узлах нагрузки; симметрирование режима; улучшение статической и динамической устойчивости электропередач. ИРМ подключаются к узлам нагрузки параллельно и подразделяются на две группы. Первая группа - синхронные генераторы станций, отдающие реактивную мощность в сеть, синхронные (динамические) компенсаторы – для плавного регулирования как в режиме генерирования, так и потребления, синхронные двигатели. Вторая группа – статические ИРМ (конденсаторные батареи, насыщающиеся реакторы в зависимости приложенного к ним напряжения в точке подключения, устройства на базе преобразователей с искусственной коммутацией тиристоров и т.д). В электроэнергетике для компенсации реактивной мощности применяют косинусные конденсаторы, работающие на частоте 50 Гц. Их мощность, измеряемая в реактивных киловольт-амперах (квар) составляет от 10 до 100 квар. Практически они собираются в батареи и обеспечивают быстрого, но ступенчатое регулирование с генерацией высших гармоник тока. Коммутация до 1 кВ выполняется обычными контакторами, в сетях 6-10 кВ и выше - с помощью тиристорных ключей переменного тока. Синхронные компенсаторы (СК) в отличие от косинусных конденсаторов обеспечивают плавное, но медленное регулирование напряжения до |
