потери. Потери. Компенсация мощность электроснабжение измерительный
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
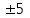 % номинального значения из-за постоянных времени системы возбуждения, а также для генерирования и потребления реактивной мощности. СК применяются в основном в узлах нагрузки, изменяющейся в широких пределах. СК это электрическая машина, работающая в режиме холостого хода (без активной нагрузки) с трех фазным неподвижным статором и вращающимся ротором, на котором находится обмотка возбуждения. СК, включенный в систему без возбуждения, потребляет реактивную мощность (индуктивный режим). При включении возбуждения и увеличении тока ротора СК переходит в режим генерирования реактивной (емкостной) режим. Статическая характеристика СК является U-образной. Минимальная длительная допустимая реактивная мощность СК не ниже 50% номинальной мощности, так как возможна потеря статической устойчивости. Достоинством СК является положительный регулирующий эффект, т.е. способность увеличивать генерируемую реактивную мощность при снижении напряжения на его шинах. Параметрами регулирования СК является реактивная мощность и напряжение, ограниченные допустимыми диапазонами изменения % номинального значения из-за постоянных времени системы возбуждения, а также для генерирования и потребления реактивной мощности. СК применяются в основном в узлах нагрузки, изменяющейся в широких пределах. СК это электрическая машина, работающая в режиме холостого хода (без активной нагрузки) с трех фазным неподвижным статором и вращающимся ротором, на котором находится обмотка возбуждения. СК, включенный в систему без возбуждения, потребляет реактивную мощность (индуктивный режим). При включении возбуждения и увеличении тока ротора СК переходит в режим генерирования реактивной (емкостной) режим. Статическая характеристика СК является U-образной. Минимальная длительная допустимая реактивная мощность СК не ниже 50% номинальной мощности, так как возможна потеря статической устойчивости. Достоинством СК является положительный регулирующий эффект, т.е. способность увеличивать генерируемую реактивную мощность при снижении напряжения на его шинах. Параметрами регулирования СК является реактивная мощность и напряжение, ограниченные допустимыми диапазонами изменения 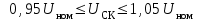 при условии выработки реактивной мощности в пределах: при условии выработки реактивной мощности в пределах: 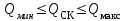 , как показано на рисунке 2.6 , как показано на рисунке 2.6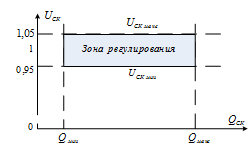 Рис. 2.6 – Зона регулирования СК Регулирование напряжения 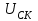 в зоне поддерживается с заданным статизмом. в зоне поддерживается с заданным статизмом.Совершенствование систем возбуждения синхронных компенсаторов (СК) средней мощности напрямую связано с нечетким управлением в виду отсутствия математического описания объекта. Существующие четкие регуляторы напряжения СК реализует собой комбинированный принцип регулирования: принцип регулирования по отклонению напряжения на шинах и принцип регулирования по возмущению реактивного тока статора с коррекцией по положительной производной тока ротора СК. Введение положительной производной по току ротора уменьшает провал напряжения в случае отсутствия демпферной обмотки СК средней мощности. Устройство формирования сигнала формирует реактивную составляющую тока статора для уменьшения времени восстановления напряжения на шинах статора при переменной нагрузке. Отрицательная жесткая обратная связь парирует влияние неконтролируемых возмущений. Применение ПИД-закона регулирования в регуляторе напряжения не всегда оправдано. Интеграл в законе регулирования устраняет ошибку регулирования в статике, но вносит отставание по фазе. Дифференциал в законе регулирования за счет фазового опережения, компенсирует отставание по фазе, но не достаточно эффективно. Для устранения данного недостатка предлагается замена классического закона управления на нечеткое управление СК, которое является наиболее перспективным направлением современной теории управления [27]. Контуры регулирования на основе нечеткой логики легко реализовать и настраивать. При этом обеспечивается лучшее качество управления: отсутствие перерегулирования и высокое быстродействие. Рассмотрим структурную схему САР с нечетким регулятором напряжения, которая приведена на рисунке 2.7. 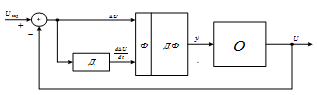 Рис. 2.7 – Структурная схема САР с нечетким регулятором напряжения Проектирование нечеткого регулятора напряжения СК для поддержания напряжения в заданном диапазоне предполагает выбор лингвистических переменных, терм-множеств по каждой переменной, формирование базы знаний (БЗ) или матрицы решений, импликации, композиции и правила приведение к четкости [27]. БЗ может формироваться: а) на лингвистической (качественной) информации, поступающей от экспертов, в форме продуктивных правил; б) на численной (количественной) информации, полученной от измерительных устройств (датчиков). в) с помощью оптимальной траектории, рассчитанной по принципу максимума, и коррекции настроек ПИД-регулятора нечеткими регуляторами; Проектирование нечеткого регулятора напряжения предполагает следующие лингвистические переменные: отклонение напряжения на статоре СК ( 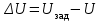 ), производную отклонения напряжения ( ), производную отклонения напряжения (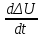 ) и ток возбуждения ротора СК. Вектор входных переменных нечеткого регулятора ) и ток возбуждения ротора СК. Вектор входных переменных нечеткого регулятора 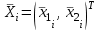 , где , где 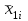 – мгновенное значение отклонения напряжения – мгновенное значение отклонения напряжения  ; ; 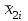 – мгновенное значение производной отклонения напряжения – мгновенное значение производной отклонения напряжения  ; ; 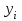 – мгновенное значение тока возбуждения ротора СК. – мгновенное значение тока возбуждения ротора СК.Зададимся описанием лингвистических переменных: 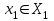 , , 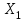 – линейное терм-множество отклонений напряжения: очень отрицательное большое (ООБ), отрицательное большое (ОБ), отрицательное среднее (ОС), отрицательное малое (ОМ), очень отрицательное малое (ООМ), норма (Н), очень положительное малое (ОПМ), положительное малое (ПМ), положительное среднее (ПС), положительное большое (ПБ), очень положительное большое (ОПБ); – линейное терм-множество отклонений напряжения: очень отрицательное большое (ООБ), отрицательное большое (ОБ), отрицательное среднее (ОС), отрицательное малое (ОМ), очень отрицательное малое (ООМ), норма (Н), очень положительное малое (ОПМ), положительное малое (ПМ), положительное среднее (ПС), положительное большое (ПБ), очень положительное большое (ОПБ); 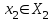 , , 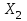 – линейное терм-множество производных отклонения напряжения: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ; – линейное терм-множество производных отклонения напряжения: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ;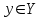 , , 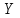 – линейное терм-множество тока ротора СК: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ. – линейное терм-множество тока ротора СК: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ.На рисунке 2.8 приведены линейные терм-множества по отклонению напряжения, производной отклонения напряжения и линейные терм-множества тока ротора СК. С целью компактной записи продуктивных правил лингвистической информации составлена матрица решений, которая приведена на рисунке 2.9. Рассмотрим нечеткий вывод i-фрагмента матрицы решений: П1: если 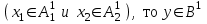 ; ;П2: если 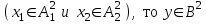 , ,где 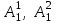 – термы Н и ООМ, соответственно, лингвистической переменной отклонения напряжения; – термы Н и ООМ, соответственно, лингвистической переменной отклонения напряжения; 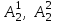 – термы Н и ПОМ, соответственно, лингвистической переменной производной отклонения напряжения; – термы Н и ПОМ, соответственно, лингвистической переменной производной отклонения напряжения; 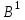 и и 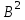 – термы i-фрагмента дефаззификатора. – термы i-фрагмента дефаззификатора.Фаззификация на синглетонной базе i-фрагмента матрицы решений: 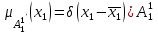 ; ;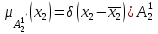 ; ;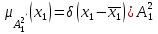 ; ;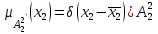 , ,где 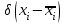 – – 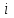 -дельта-функция (синглетон); -дельта-функция (синглетон); 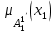 – степень принадлежности – степень принадлежности 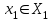 подмножеству подмножеству 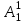 ; ; 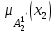 – степень принадлежности – степень принадлежности 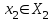 подмножеству подмножеству 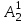 ; ; 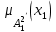 – степень принадлежности – степень принадлежности 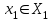 подмножеству подмножеству 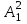 ; ; 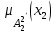 – степень принадлежности – степень принадлежности 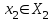 подмножеству подмножеству 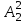 . .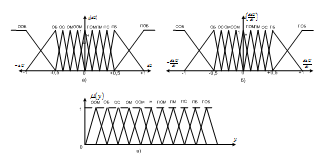 Рис. 2.8 – Линейные терм-множества: а) по отклонению напряжения; б) по производной отклонения напряжения; в) функции принадлежности тока возбуждения СК 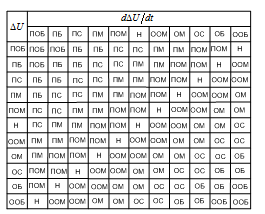 Рис. 2.9 – Матрица решений Импликация i-фрагмента матрицы решений: 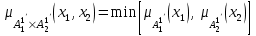 ; ;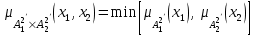 . .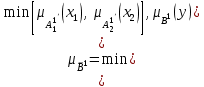 ; ;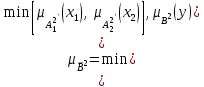 , ,где 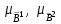 – функции принадлежности усеченных множеств – функции принадлежности усеченных множеств 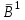 (ПМ) и (ПМ) и 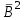 (ПОМ). (ПОМ). Композиция i-фрагмента матрицы решений 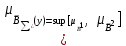 , ,где 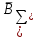 – результирующее нечеткое множество. – результирующее нечеткое множество.Для устранения нечеткости окончательного результата (тока возбуждения ротора СК) существует несколько методов: метод центра максимума (метод среднего), метод наибольшего значения (метод максимума), метод центроида [27]. Рассмотрим дефаззификацию (метод центроида). Необходимо определить минимальную координату абсцисс, соответствующей максимальной высоте нелинейного объединенного усеченного множества. Известны разные формулы расчета координат ЦТ фигуры по методу центроида. Одна из них (2.22) приведена в [27]. 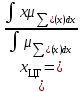 . (2.22) . (2.22)Формула (2.22) удобна в случае, когда функции принадлежности дефаззификатора есть синглетоны. Известна формула (2.23) вычисления абсциссы ЦТ линейных объединенных усеченных множеств (фигуры), образованных из линейных функций принадлежности дефаззификатора, с фиксацией координат характерных точек [27]. 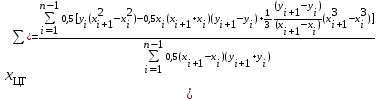 , (2.23) , (2.23)где 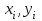 – координаты характерных точек элементарных фигур, определяющих границы – координаты характерных точек элементарных фигур, определяющих границы 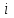 -результирующего нечеткого множества (фигуры). -результирующего нечеткого множества (фигуры).Расчет координат ЦТ фигуры по формуле (2.23) требует знания координат характерных точек элементарных фигур и имеет фиксированную точность, которая зависит от формы фигуры. В [27] приводятся формулы (2.24) и (2.25) определения координат ЦТ фигуры, которые предполагают равномерное разбиение фигуры по оси абсцисс с построением 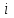 -прямоугольников разной высоты. -прямоугольников разной высоты. 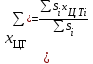 ; (2.24) ; (2.24) 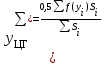 , (2.25) , (2.25)где 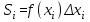 – площадь i-фигуры (прямоугольника); – площадь i-фигуры (прямоугольника); 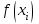 – высота i-прямоугольника; – высота i-прямоугольника; 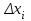 – ширина i-прямоугольника; – ширина i-прямоугольника; 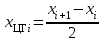 – значение абсциссы ЦТ – значение абсциссы ЦТ 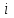 -фигуры. -фигуры.Недостатком применения формул (2.24) и (2.25) является большой объем вычислений и снижение быстродействия формирования управляющего воздействия на объект. С целью повышения быстродействия расчета координат ЦТ и снятия ограничений на функцию 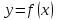 , рассмотрим приближенный алгоритм на основе неравномерного разбиения по оси абсцисс фигуры объединенного усеченного множества с построением , рассмотрим приближенный алгоритм на основе неравномерного разбиения по оси абсцисс фигуры объединенного усеченного множества с построением 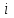 -прямоугольников равной площади и разной высоты. -прямоугольников равной площади и разной высоты. Пусть объединенное усеченное множество описывается функцией 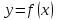 и сложная фигура расположена на интервале [a, b] по оси абсцисс. и сложная фигура расположена на интервале [a, b] по оси абсцисс.Предлагается следующий алгоритм вычисления координат ЦТ фигуры: – рассчитываем площадь S сложной фигуры; – разбиваем сложную фигуру на n простых фигур с неравномерным разбиением по оси абсцисс, причем площади этих фигур должны быть одинаковыми и равными 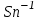 . Число разбиений n определяется из соотношения . Число разбиений n определяется из соотношения 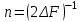 , где , где 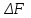 – абсолютная погрешность воспроизведения функции – абсолютная погрешность воспроизведения функции 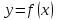 ; ;– задаемся приращением 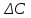 изменения координаты абсциссы, которое должно быть хотя бы на порядок меньше, чем изменения координаты абсциссы, которое должно быть хотя бы на порядок меньше, чем 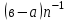 ; ;– определяем координаты точек абсцисс в интервале разбиения 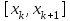 , где , где 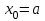 ; ; 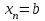 ; ; 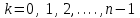 . Для определения точек разбиения . Для определения точек разбиения 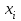 подсчитывается значение площади подсчитывается значение площади 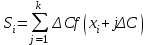 и сравнивается со значением и сравнивается со значением 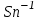 . Увеличиваем значение . Увеличиваем значение 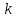 до выполнения условия до выполнения условия 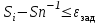 , где , где 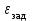 – заданная точность. Граница – заданная точность. Граница 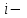 интервала определяется по формуле интервала определяется по формуле 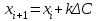 . Указанная процедура выполняется на всем отрезке [a, b] и определяет координаты . Указанная процедура выполняется на всем отрезке [a, b] и определяет координаты 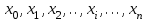 . В пределах каждого интервала . В пределах каждого интервала 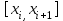 функция функция 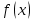 аппроксимируется постоянными значениями аппроксимируется постоянными значениями 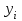 ; ;– определяем абсциссу и ординату ЦТ объединенного усеченного множества по формулам (2.26) и (2.27), соответственно: 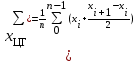 ; (2.26) ; (2.26)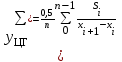 . (2.27) . (2.27)Приведенный алгоритм вычисления координат ЦТ был проверен на фигуре объединенного усеченного множества, показанного на рисунке 2.10. 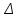 C = 0,02; C = 0,02;n = 8; 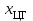 = 1,691; = 1,691; 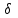 = 2,29%; = 2,29%;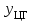 = 1,044; = 1,044; 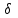 = 1,36%; = 1,36%;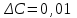 n = 8; 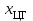 = 1,705; = 1,705; 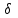 = 1,49%; = 1,49%;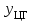 = 1,013; = 1,013; 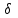 = 1,68%; = 1,68%;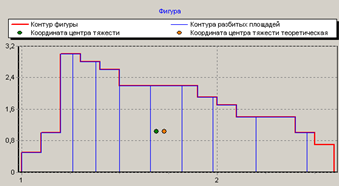 Рис. 2.10 – Пример фигуры Таким образом, можно сделать следующие выводы: – формула расчета координат ЦТ объединенного линейного усеченного множества (2.23) предполагает линейные функции принадлежности дефаззификатора с фиксацией координат характерных точек элементарных фигур; – формулы расчета координат ЦТ (2.26) и (2.27) объединенного усеченного множества предполагают как линейные, так и нелинейные функции принадлежности дефаззификатора, являются универсальными и могут широко применяться при проектировании нечеткого регулятора. Рассмотрим имитационное моделирование САР. Для проверки работоспособности нечеткого регулятора напряжения разработана цифровая модель системы автоматического регулирования напряжения статора СК мощностью 0,01 МВт. СК представлен в виде уравнений Парка-Горева в модификации Л.П.Веретенникова. Дифференциальные уравнения записаны через внутреннюю ЭДС в анормальной системе относительных единиц. Мгновенный вектор напряжения на шинах СК определен по методу двух узлов [8]. Нагрузкой объекта является асинхронный короткозамкнутый двигатель мощностью 0,005 Мвт. Математическое описание установки приведено в приложении А. На рисунке 2.11 приведена осциллограмма процесса возбуждения СК и пуска асинхронного двигателя от СК. |
