теория АиГ. АиГ ЛЭТИ 2021 часть 1. Комплексные числа Определение
 Скачать 19.97 Kb. Скачать 19.97 Kb.
|
|
Комплексные числа Определение Комплéксное число – выражение вида a+bi, где a, b – вещественные числа, i – специальный символ. При этом a называют вещественной частью числа z, b – мнимой частью числа z. Допустим, что   Тогда Тогда 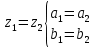 Иными словами, два комплексных числа равны тогда и только тогда, когда равны их вещественные части и мнимые части. Геометрическая интерпретация комплексных чисел Если множество вещественных чисел удобно изображать в виде прямой, то множество комплексных чисел – в виде плоскости. Каждое число a+bi изображают в виде точки с координатами (a, b). При этом ось абсцисс соответствует множеству вещественных чисел, ордината точки равна мнимой части соответствующего комплексного числа. Примеры (здесь и далее примеры подразумевают разбор на доске, одновременно беседу со студентами). Изобразить на плоскости комплексные числа -3 2i -2+i 3 - 5i Сложение и вычитание комплексных чисел  Тогда:   Иными словами, при сложении комплексных чисел отдельно складываются их вещественные части, и отдельно складываются мнимые части. Геометрическая интерпретация для тех, кто знаком с координатным подходом в геометрии: сложение комплексных чисел соответствует сложению векторов и сложению их соответствующих координат. Примеры Найти сумму (3 - 2i) + (4 + 3i) (2 + i) - (4 - i) Умножение комплексных чисел Комплексные числа умножают по правилам, принятым для умножения многочленов, но вместо выражения  пишем -1. пишем -1.В общем виде формула такова: (  Примеры (3i+1)(2i-7)   Примечание: куб комплексного числа с ненулевой мнимой частью может оказаться вещественным числом. Примечание: куб комплексного числа с ненулевой мнимой частью может оказаться вещественным числом.Сопряжение комплексных чисел Определение Сопряженным к комплексному числу a+bi называют число a – bi. В общем виде комплексное число, сопряженное к числу  , обозначается , обозначается  . .Примеры Решите уравнение   (1-2i)  Примечание: на примере таких задач удобно показывать смысл метода неопределенных коэффициентов. Деление комплексных чисел Для деления  удобно знаменатель домножить на сопряжённое комплексное число, тогда задача будет сведена к делению на вещественное число. удобно знаменатель домножить на сопряжённое комплексное число, тогда задача будет сведена к делению на вещественное число.Примеры 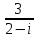 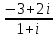 Возведение в степень комплексных чисел В приведенных ниже примерах удобно представить степень в виде «степень в степени». 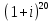  Тригонометрическая форма. Модуль и аргумент комплексного числа Если комплексное число z изобразить в виде точки на плоскости, то для некоторых задач удобно задать его с помощью двух параметров: расстояния до начала координат и угла между положительной полуосью оси абсцисс и радиус-вектором на точку z. В таком случае модуль обозначают  , аргумент обозначают Arg z. , аргумент обозначают Arg z.Аргумент комплексного числа находится на интервале [0, 2π) Примеры Найдите модули и аргументы чисел. 2 -6 i 1 + i   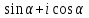 , где α - произвольное число. , где α - произвольное число. Тригонометрическая форма комплексного числа Комплексное число z можно записать в виде 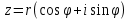 , где r – модуль числа, φ – аргумент. , где r – модуль числа, φ – аргумент.Эту форму записи называют тригонометрической формой. Запись вида z = a + bi называют алгебраической формой. Иногда для краткости вместо 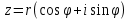 пишут пишут  . При такой форме записи для φ = π получаем . При такой форме записи для φ = π получаем Интересно, что в этой формуле участвуют сразу три известные константы: e, i, π. Переход от алгебраической формулы z = a + bi к тригонометрической форме 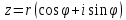 осуществляется по формулам (для вычисления аргумента часто требуются дополнительные соображения, в том числе геометрические): осуществляется по формулам (для вычисления аргумента часто требуются дополнительные соображения, в том числе геометрические): Примеры Представьте числа в тригонометрической форме 1 -2 2i 1 + i 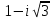 1 + 2i 1 + 2i-1 - 3i Умножение и возведение в степень комплексных чисел в тригонометрической форме Пусть 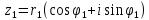 , ,  . .Перемножив эти два числа и воспользовавшись тригонометрической формулой для суммы, получим:  Иными словами, при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а их аргументы складываются. Кроме того, если 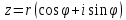 , то по формуле умножения комплексных чисел , то по формуле умножения комплексных чисел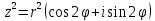 . .Кроме того,  , , то есть  и, продолжая этот процесс домножения на z далее, получим:  Таким образом, при возведении в степень комплексных чисел в тригонометрической форме их модули возводятся в эту степень, а их аргументы умножаются на показатель степени. Поэтому для возведения в степень часто бывает удобнее сначала перевести комплексное число в тригонометрическую форму. Часто для упрощения вычислений отдельно рассматривают комплексные числа с модулем, равным 1. В таком случае формула для степени выглядит так: 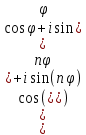 (формула Муавра) (формула Муавра)Примечание. Эта формула имеет много направлений применения – например, нахождение формул синуса и косинуса кратных углов, извлечение корней степени n из комплексного числа. Примеры Переведите в тригонометрическую форму (повторение) 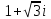 3 + 4i 1 - 2i Примечание: не забывайте про область значений аргумента. Он не бывает отрицательным. Найдите значение выражений 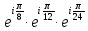 (напоминаем, что (напоминаем, что  означает означает 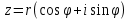 ) ) 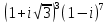 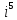 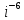  |
