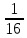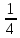09.02.07 КИМы. Комплект контрольнооценочных материалов для оценки результатов освоения по учебной дисциплине ен. 03 Теория вероятностей и математическая статистика
 Скачать 44.92 Kb. Скачать 44.92 Kb.
|
|
Министерство образования Ставропольского края Частное профессиональное образовательное учреждение Ставропольский колледж экономики и управления «Бизнестранс» «УТВЕРЖДАЮ» Директор ЧПОУ СКЭиУ «Бизнестранс» _____________/В.С. Степанова/ «____» ____________ 2021 г. Комплект контрольно-оценочных материалов для оценки результатов освоения по учебной дисциплине ЕН.03 Теория вероятностей и математическая статистика для специальности 09.02.07. Информационные системы и программирование Ставрополь, 2021
Разработчик: Сапрунова А.А., ст. преподаватель Утверждено Учебно-методическим советом от 12.02.2021 года, протокол заседания №4 1. Общие положения Контрольно-измерительные материалы предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ЕН.03 Теория вероятностей и математическая статистика. КИМ включают контрольные материалы для проведения промежуточной аттестации в форме дифференцированного зачета 2. Планируемые результаты освоения дисциплины: Процесс изучения дисциплины направлен на формирование элементов следующих компетенций в соответствии с ФГОС СПО и ОПОП СПО по данной специальности: общих компетенций (ОК), включающих в себя способность: ОК 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам ОК.02 Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности ОК.04 Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами ОК.05 Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста ОК 09. Использовать информационные технологии в профессиональной деятельности ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках Результаты освоения дисциплины, подлежащие проверке
3. Условия выполнения заданий
4. Критерии оценки выполнения заданий Задания 1-7
Задания 8-10
5. Шкала пересчета суммарного балла за выполнение зачетной работы в целом
Краткая инструкция для обучающихся На выполнение письменной зачетной работы по учебной дисциплине «ЕН.03 Теория вероятностей и математическая статистика» дается 2 академических часа (90 минут). Зачетная работа состоит из 2-х частей: обязательной и дополнительной. При выполнении большинства заданий обязательной части требуется представить ход решения и указать полученный ответ, и только в нескольких заданиях достаточно представить ответ. При выполнении любого задания дополнительной части описывается ход решения и дается ответ. Правильное выполнение любого задания обязательной части оценивается одним баллом, правильное выполнение каждого задания дополнительной части - тремя баллами. Баллы указываются в скобках около номера задания. Если приводится неверный ответ или ответ отсутствует, ставится 0 баллов. Баллы, полученные за все выполненные задания, суммируются. Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов. Перед началом работы внимательно изучите критерии оценивания и обратите внимание, что начинать работу следует с заданий обязательной части. И только после того, как Вы наберете необходимое количество баллов для удовлетворительной оценки, можете переходить к заданиям дополнительной части, чтобы повысить оценку до четырех или пяти. Желаем успехов! Шкала пересчета зачетной экзаменационной работы в целом Если студент набрал менее 4 баллов в обязательной части, решение заданий дополнительной части не проверяется.
Вариант 1 (1 балл). Бросают игральную кость с 6 гранями и запускают волчок, имеющий 8 граней. Сколькими различными способами могут они упасть? (1 балл). Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5. (1 балл). Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что они различны набрал их наудачу. Какова вероятность того, что номер набран правильно? (1 балл). Слово «спаниель» составлено из букв разрезной азбуки. Наудачу извлекают карточки и складывают в ряд друг за другом в порядке появления. Какова вероятность получить при этом слово «апельсин», (1 балл). На тепловой электростанции 15 сменных инженеров, из них три женщины. В смену заняты четыре человека. Найти вероятность того, что в случайно выбранную смену будут работать два мужчины и две женщины. (1 балл). Результаты статистических исследований в медицине показывают, что если пациент боле некоторым инфекционным заболеванием, то тест даст положительный результат для 90%, а если не болен, то тест может дать положительный результат для 7% проверяемых. Этому виду инфекции, согласно статистическим исследованиям, подвержено только 0,3% населения. Пусть некоторому случайно выбранному пациенту сделан анализ и получен положительный результат. Найдите вероятность того, что он действительно заражен этим видом инфекции. (1 балл). Для данного баскетболиста вероятность попадания мяча в кольцо при каждом броске равна 0,4. Определите наиболее вероятную ситуацию – попадание трех мячей при четырех бросках мяча или попадание четырех мячей при пяти бросках мяча, если броски считаются независимыми. Дополнительная часть (3 балла). Составьте закон распределения суммы числа очков, выпавших при бросании двух игральных костей. Найдите моду, медиану, математическое ожидание. ( 3 балла) Случайная величина задана законом распределения
Найти дисперсию и среднеквадратическое отклонение ДСВ Х. (3 балла) для данной выборки 2, 4, 2, 4, 3, 3, 3, 2, 0, 6, 1, 2, 3, 2, 2, 4, 5, 6, 6, 1, 1, 2, 3, 6 постройте вариационный ряд. Составьте эмпирическую функцию распределения. Вариант 2 Обязательная часть (1 балл). Сколькими способами можно составить трехцветный флаг с горизонтальными полосами одинаковой ширины, если имеется материя 7 различных цветов? (1 балл). В коробке находятся 6 новых и 2 израсходованные батарейки для карманного фонарика. Какова вероятность того, что две вынутые из коробки наудачу батарейки окажутся новыми? (1 балл). Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что они различны набрал их наудачу. Какова вероятность того, что номер набран правильно? (1 балл). На трех карточках написаны буквы У, К, Ж. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «ЖУК»? (1 балл). Два станка работают независимо друг от друга, причем вероятность бесперебойной работы первого станка в течение определенного времени равна 0,8, а другого – 0,85. Какова вероятность выхода из строя обоих станков в течение данного промежутка времени? (1 балл). В ящике находятся детали, из которых 12 изготовлены на первом станке, 20- на втором и 16 – на третьем. Вероятности того, что детали, изготовленные на первом, втором и третьем станках, стандартные, соответственно равны 0,9; 0,8 и 0,6. Найдите вероятность того, что взятая наугад деталь окажется стандартной. (1 балл). Среди коконов некоторой партии содержится 20% цветных. Какова вероятность того, что среди шести случайно отобранных из партии коконов четыре окажутся цветными? Дополнительная часть (3 балла). Составьте закон распределения произведения числа очков, выпавших при бросании двух игральных костей. Найдите моду, медиану, математическое ожидание. ( 3 балла) Закон распределения случайной величины Х задан таблицей
Найти математическое ожидание Х и дисперсию (3 балла) Для данной выборки 5, 8 ,7, 6, 7, 8, 9, 10, 5, 8, 7, 5, 6, 6, 9, 7, 8, 10, 9, 8, 5, 6, 8 постройте вариационный ряд. Составьте эмпирическую функцию распределения. |