Вопрос №16
V2
|
Rang 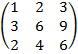 ? ?
|
0
|
-1
|
0
|
1
|
0
|
2
|
0
|
3
|
0
|
Сызықты тәуелсіз жолының саны (Числу линейно независимых строк
|
0
|
Ең үлкен нөлден ерекше минордың ретіне (Порядку наибольшего минора отличного от нуля
|
0
|
4
|
Вопрос №17
V2
|
4-белгісізден құралған 4-сызықты коэффициентері тұрақты теңдеулер жүйесі берілген. Бүл жүйенің неше шешімі болу мүмкін.
(Задана система из 4-х линейных уравнений с постоянными коэффициентами с 4-мя неизвестными. Сколько решений может иметь система?
|
0
|
1 немесе 2 (1 или 2
|
0
|
1
|
0
|
Кезгелген 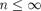 саны (Любое саны (Любое 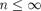 число число
|
0
|
4
|
0
|
Шексіз (Бесконечное число
|
0
|
3
|
0
|
Шешім жоқ (Ни одного
|
Вопрос №18
V2
|
Параллель жазықтықтардың сипаттарын көрсетіңіз
(Укажите свойства параллельных плоскостей
|
0
|
Егер түзулер бір жазықтықта жатса және қиылысатын болса, олар параллель болады (Если прямые лежат в одной плоскости и пересекаются, они параллельны
|
0
|
Екі параллель жазықтықтың арасына салынған параллель түзулердің кесінділері тең (Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны
|
0
|
Егер екі параллель жазықтықты үштен бірі кесіп өтсе, онда олардың қиылысу түзулері параллель болады
(Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
|
0
|
Параллель жазықтықтар бұрыштың бүйірлерін пропорционалды бөліктерге кеседі. (Параллельные плоскости рассекают стороны угла на пропорциональные части.
|
0
|
Егер екі түзу бір нүктеден өтіп, қиылысатын болса, олар параллель болады
(Если две прямые проходят через одну точку и пересекаются, они параллельны
|
0
|
Егер түзулер қиылыспаса және бір жазықтықта жатпаса, онда олар параллель болады (Если прямые не пересекаются и не лежат в одной плоскости, то они параллельны
|
Вопрос №19
V2
|
А(1,3,0), В(4,-1,2), С(3,0,1) нүктелері арқылы өтетін жазықтықтың теңдеуін жаз.
(Написать уравнение плоскости, проходящей через точки А(1,3,0), В(4,-1,2), С(3,0,1).
|
0
|
2x + y − z = 2
|
0
|
2x + y − z − 5 = 0
|
0
|
2x + y − z = 5
|
0
|
x + 0.5y – 0.5z − 1 = 0
|
0
|
x + y − z − 10 = 0
|
0
|
x + 0.5y – 0.5z – 2.5 = 0
|
Вопрос №20
V2
|
k 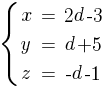 түзуінен және B = {2; -3; 1} нүктесі арқылы өтетін жазықтықтың теңдеуін құрыңдар: түзуінен және B = {2; -3; 1} нүктесі арқылы өтетін жазықтықтың теңдеуін құрыңдар:
(Составить уравнение плоскости, проходящей через прямую k:
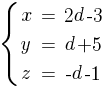 и точку B = {2; -3; 1}. и точку B = {2; -3; 1}.
|
0
|
2x + 3y + 7z – 12 = 0
|
0
|
2x + 3y + 7z – 2 = 0
|
0
|
2x + 3y + 7z = 12
|
0
|
2x - y + 5z = -16
|
0
|
2x + 3y + 7z = 0.
|
0
|
2x + 3y + 7z – 2 = 0.
|
Вопрос №21
V2
|
А(2;3) нүктесі арқылы өтетін түзу теңдеуі келесі түрде жазылады: (Уравнение прямой, проходящей через точку А(2;3) имеет вид:
|
0
|
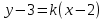
|
0
|
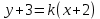
|
0
|
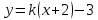
|
0
|
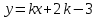
|
0
|
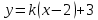
|
0
|
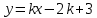
|
Вопрос №22
V2
|
А(-1;3) нүктесі арқылы өтетін түзу теңдеуі келесі түрде жазылады: (Уравнение прямой, проходящей через точку А(-1;3) имеет вид:
|
0
|
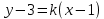
|
0
|
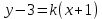
|
0
|
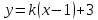
|
0
|
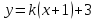
|
0
|
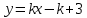
|
0
|
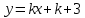
|
Вопрос №23
V2
|
А(0;1) нүктесі арқылы өтіп, y=2x+3 сызығына параллель болатын теңдеуді жазыңыз:
(Уравнение прямой, проходящей через точку А(0;1) параллельно прямой y=2x+3:
|
0
|
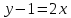
|
0
|
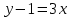
|
0
|
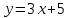
|
0
|
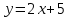
|
0
|
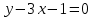
|
0
|
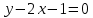
|
Вопрос №24
V2
|
М(3;4) нүктесі арқылы өтіп, y=3x-1 сызығына параллель болатын теңдеуді жазыңыз:
(Уравнение прямой, проходящей через точку М(3;4) параллельно прямой y=3x-1:
|
0
|
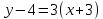
|
0
|
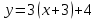
|
0
|
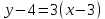
|
0
|
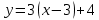
|
0
|
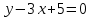
|
0
|
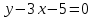
|
Вопрос №25
V2
|
А(1;2) және В(3;4) нүктелері арқылы өтетін түзу теңдеуін жазыңыз: (Уравнение прямой, проходящей через точки А(1;2) и В(3;4) имеет вид:
|
0
|
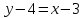
|
0
|
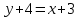
|
0
|
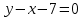
|
0
|
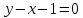
|
0
|
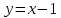
|
0
|
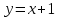
|
Вопрос №26
V2
|
А(2;-3) және В(3;-4) нүктелері арқылы өтетін түзу теңдеуін жазыңыз: (Уравнение прямой, проходящей через точки А(2;-3) и В(3;-4), имеет вид:
|
0
|
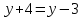
|
0
|
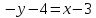
|
0
|
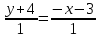
|
0
|
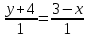
|
0
|
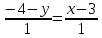
|
0
|
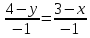
|
Вопрос №27
V2
|
Ұсынылған матрицалардың ішінен вектор – бағанды таңдаңыз
(Выберите вектор – столбец из числа предложенных матриц
|
0
|
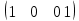
|
0
|
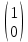
|
0
|
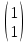
|
0
|
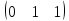
|
0
|
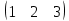
|
0
|

|
Вопрос №28
V2
|
Ұсынылған матрицалардың ішінен вектор – жолды таңдаңыз
(Выберите вектор – строку из числа предложенных матриц
|
0
|
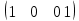
|
0
|
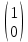
|
0
|
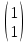
|
0
|
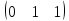
|
0
|
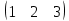
|
0
|
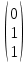
|
Вопрос №29
V2
|
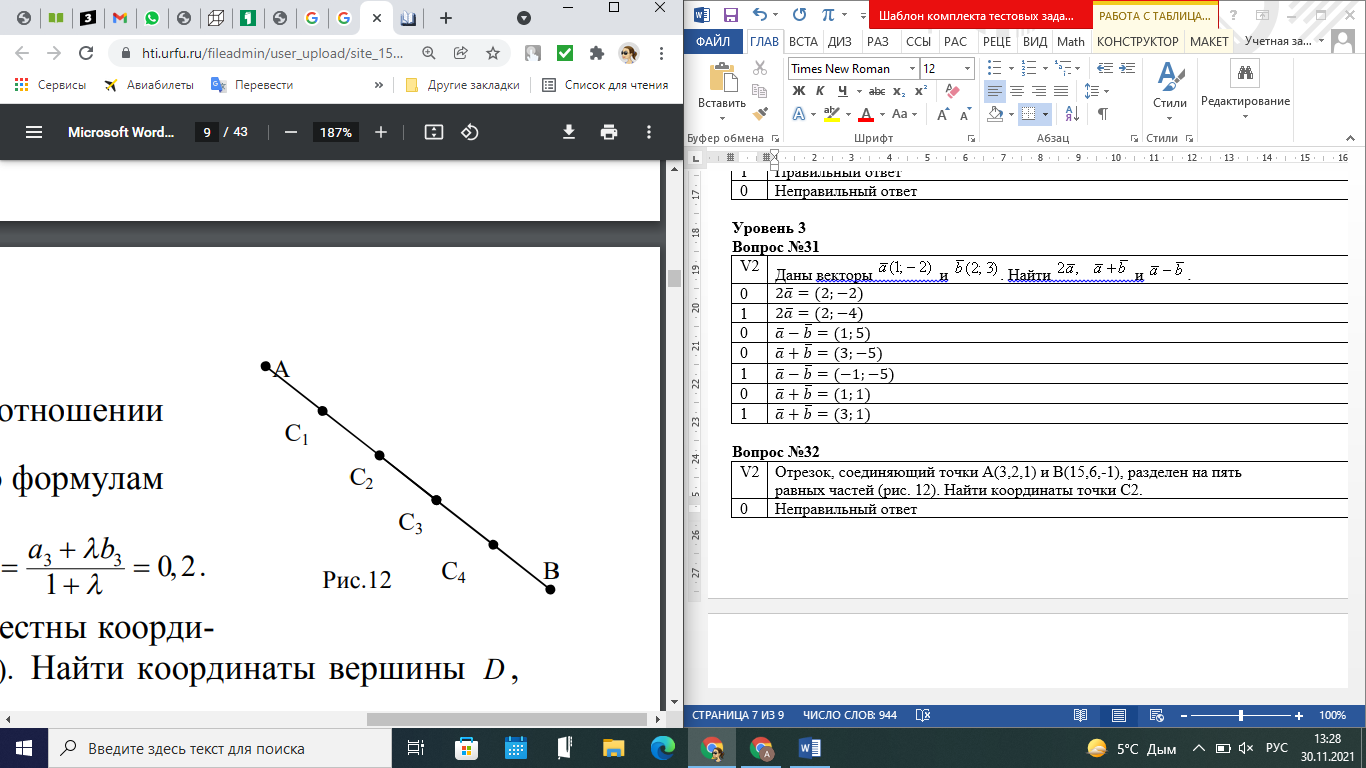
АВ кесіндісі тең пес бөлікке бөлінді, 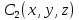 нүктесін табыңыз. нүктесін табыңыз.
(Отрезок, соединяющий точки A(3,2,1) и B(15,6,-1), разделен на пять равных частей (рис. 12). Найти координаты точки 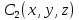 . .
|
0
|
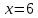
|
0
|
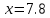
|
0
|
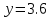
|
0
|
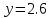
|
0
|
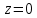
|
0
|
| |
 Скачать 1.16 Mb.
Скачать 1.16 Mb.