конденсатор. Конденсатор (ёмкость)
 Скачать 45.26 Kb.
|
|
Конденсатор (ёмкость) Конденсатор (ёмкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:  Величина ёмкости измеряется в фарадах (Ф). 1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.  1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: - пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке. Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома. Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой. Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.  Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качествефильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструированиичастотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xc или Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением: 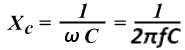 Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора. Теперь представьте, что дифференцирующая цепь, это – описанный на сайте делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.  То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо - АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2. Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе. Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке - оранжевого цвета, и частота среза равная значению f1. Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности. Параллельное соединение конденсаторов Общая ёмкость конденсаторов при параллельном соединении равна их сумме. 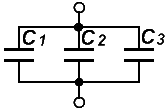 ,  Последовательное соединение конденсаторов Величина, обратно пропорциональная общей ёмкости конденсаторов при последовательном соединении равна сумме величин, обратно пропорциональных их ёмкости.  ,  Для двух последовательно соединенных конденсаторов их общая ёмкость равна: 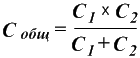 |