средние и показатели вариации. Средние величины средняя величина
 Скачать 135.35 Kb. Скачать 135.35 Kb.
|
|
5.3. СРЕДНИЕ ВЕЛИЧИНЫ Средняя величина – это обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени. Средние величины исчисляются очень часто: средний уровень заработной платы, средняя оценка студентов по определенной учебной дисциплине и др. Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности. Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. Вычисление среднего – один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности. Средние величины делятся на два больших класса: степенные средние; к ним относятся такие наиболее известные и часто применяемые виды, как средняя арифметическая, геометрическая, квадратическая, хронологическая и т.д.; структурные средние, в качестве которых рассматриваются мода и медиана. Выбор вида степенной средней зависит от содержания логической формулы расчета осредняемого признака и имеющихся исходных данных. Степенные средние в зависимости от предоставления исходных данных исчисляются в двух формах: простой (считается по несгруппированным данным) и взвешенной (применяется для сгруппированных данных). 5.3.1. Средняя арифметическая Средняя арифметическая применяется, если известны значения осредняемого признака (х) и количество единиц совокупности с определенным значением признака (f). Средняя арифметическая применяется в форме простой средней ивзвешенной средней. Исходной определяющей формой служит простая средняя. Средняя арифметическая простая применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака и определяется по формуле  (5.8) (5.8)где 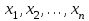 – индивидуальные значения варьирующего признака (варианты); – индивидуальные значения варьирующего признака (варианты); п – число единиц совокупности. Далее пределы суммирования в формулах указываться не будут. Например, требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.: 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 31; 20; 18; 19; 20. Средняя арифметическая простая рассчитывается по формуле (4.8), шт.: 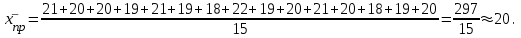 Средняя арифметическая взвешенная применяется, если каждое значение признака х встречается несколько раз, т.е. для каждого х значение f≠1. Данная средняя широко используется при исчислении средней на основании дискретного ряда распределения: 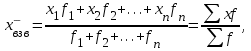 (5.9) (5.9)где f1, f2, ..., fn,– веса (частота); f – общая численность единиц совокупности. Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим их в табл. 5.1. Таблица 5.1 Распределение рабочих по выработке деталей
По формуле (5.9) средняя арифметическая взвешенная равна, шт.: 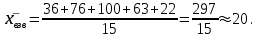 В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид: 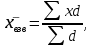 (5.10) (5.10)где 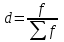 – частость, т.е. доля каждой частоты в общей сумме всех частот. – частость, т.е. доля каждой частоты в общей сумме всех частот.Если частоты подсчитывают в долях (коэффициентах), то d=1, и формула средней арифметической взвешенной имеет вид:  . (5.11) . (5.11)Расчет средней по интервальному ряду. Если исходные данные заданы в виде интервального ряда, то: закрывают открытые интервалы; 2) за значение осредняемого признака х берут середины интервалов и строят условный дискретный ряд распределения; расчет средней производится по средней арифметической взвешеной. Имеются данные о распределении рабочих цеха по стажу работы:
Каков средний стаж работы рабочего данного цеха? Строим расчетную таблицу.
Закрываем открытый интервал «до 5». Ширина ближайшего закрытого интервала равна 5 годам, следовательно, наш интервал примет вид от 0 до 5. Аналогично открытый интервал «20 и выше» примет вид 20-25. Находим середину каждого интервала и принимаем ее за значение х. Исчисляем значения xf и сумму этих значений, необходимую для расчета средней арифметической взвешенной, заносим результаты в расчетную таблицу. Определяем средний стаж рабочего: 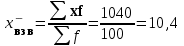 лет. лет.Рабочий данного цеха отработал в среднем 10,4 года. Расчет средней по интервальному ряду распределения дает приближенный результат за счет того, что за значения х берутся не точные данные, а середины интервалов. Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет: если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого на изменится; если все индивидуальные значения признака (т.е. все варианты) увеличить или уменьшить в одно и тоже число раз (или на одно и тоже число), то средняя арифметическая увеличится или уменьшится во столько же раз (или на столько же). Использование свойств средней позволяет упростить вычисление средней арифметической. Упрощенный расчет средней (способ моментов). Для интервальных рядов с равными интервалами расчёт средней можно производить по упрощенной формуле. Алгоритм метода заключается в следующем: строится новый дискретный ряд распределения, в котором одна из вариант, имеющая наибольшую частоту приравнивается к нулю. остальные варианты нового ряда обозначаются х1 и рассчитываются по формуле: 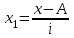 , (5.12) , (5.12)где А – значение варианты, имеющей наибольшую частоту; определяется средняя по способу моментов: 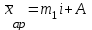 ; (5.13) ; (5.13)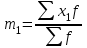 , (5.14) , (5.14)где m1 – момент 1-го порядка; Расчет средней арифметической по способу моментов иллюстрируется данными табл. 5.2. Таблица 5.2Распределение малых предприятий региона по стоимости основных производственных фондов (ОПФ)
Находим момент первого порядка  . .Затем, принимая А = 19 (величина х с наибольшей частотой) и зная, что i =2, вычисляем   = m1i + A = 0 . 2 + 19=19 тыс. руб. = m1i + A = 0 . 2 + 19=19 тыс. руб.5.3.2. Средняя гармоническая Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение xf, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим х f = w, откуда f = w / х. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.9) вместо хf подставим w, вместо f – отношение w / х и получим формулу средней гармонической взвешенной: 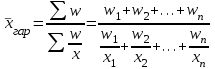 . (5.15) . (5.15)Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = х f. Например, по данным (табл. 5.3) требуется определить среднюю цену 1 кг картофеля. Таблица 5.3 Цена и выручка от реализации по трем коммерческим магазинам в октябре 2010 г.
Расчет средней цены производится следующим образом: Средняя цена, руб.  Определяющим показателем здесь является числитель этой логической формулы. Выручка от реализации w известна (числитель), а количество реализованных единиц – неизвестно, но может быть найдено как частное от деления одного показателя на другой, для чего нужно отдельно по каждому магазину разделить выручку на цену. Тогда средняя цена 1 кг картофеля, руб. по трем коммерческим магазинам может быть исчислена по формуле (5.15) средней гармонической взвешенной:  Этот же результат получится и по средней арифметической взвешенной, если в качестве весов принять количество проданных единиц (которые необходимо предварительно рассчитать), руб.: 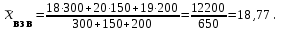 Исчисление средней гармонической взвешенной по формуле (5.15) освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу. Средняя гармоническая, также как и арифметическая, может быть не только взвешенной, но и простой. 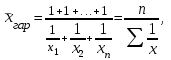 (5.16) (5.16)где х – значения осредняемого признака; n – число значений х. На практике средняя гармоническая простая применяется редко, в тех случаях, когда значения w для единиц совокупности равны. Выбор средней на основании логической формулы. Иногда по исходным данным трудно определить, чем являются показатели – численностью единиц совокупности (f ) или объемом осредняемого признака (w). В этом случае необходимо: записать логическую формулу расчета осредняемого признака, исходя из его экономического содержания; выбрать для расчета среднюю арифметическую взвешенную, если известен знаменатель логической формулы; использовать среднюю гармоническую взвешенную, если в исходных данных имеется числитель логической формулы. 5.3.3. Другие виды средних величин Для расчета среднего квадратического отклонения применяется средняя квадратическая, простая или взвешенная. Средняя квадратичекая простая используется, если каждое значение признака встречается один раз, в общем виде имеет вид: 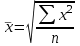 , (5.17) , (5.17)где n – число единиц совокупности. Средняя квадратичекая взвешенная применяется, если каждое значение осредняемого признака х встречается f раз: 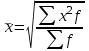 . (5.18) . (5.18)Если значения осредняемого признака известны на несколько дат внутри определенного временного периода, расчет производится по средней хронологической: 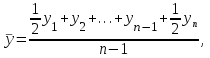 (5.19) (5.19)где y1,…,yn– значения осредняемого признака; n – число дат внутри периода, на которые заданы значения y. По средней хронологической исчисляется средняя годовая стоимость основных фондов предприятия из данных о наличии на начало каждого месяца; средний запас материальных ценностей, если известны величины запасов на определенные даты, разделенные равными интервалами; средний остаток вкладов на счетах в банке по информации на начало каждого месяца. Если значения осредняемого признака существенно отстоят друг от друга или заданы коэффициентами, то для расчета применяют среднюю геометрическую: 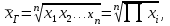 (5.20) (5.20)где n – число вариант; П – знак произведения. Пусть цены в первом полугодии ежемесячно возрастали следующим образом: в январе в 1,02 раза; феврале – в 1,04; марте – в 1,03; апреле – в 1,04; мае – в 1,02; июне – в 1,06 раза. Среднее изменение цен: 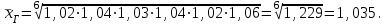 В первом полугодии цены ежемесячно возрастали в среднем в 1,035 раза, или на 3,5 %. Наиболее широкое применение средняя геометрическая получила для определения среднего темпа роста в рядах динамики. 5.3.4. Структурные средние Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. В отличие от степенных средних структурные средние имеют не обобщенное значение признака, а вполне конкретное, т.е. значение одной из вариант. К таким показателям относятся мода и медиана. Мода (Мо) – варианта, имеющая наибольшую частоту. Мода применяется для характеристики наиболее часто встречающегося значения признака: наиболее распространенного уровня заработной платы на предприятии, цены на товар с наибольшим объемом продаж, размера одежды, пользующегося наибольшим спросом. Если исходные данные представлены дискретным рядом распределения, модой является варианта с наибольшей частотой. Например, в табл. 5.1 наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в данном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей. Могут быть совокупности, где все варианты встречаются одинаково часто, т.е. моды нет, или все варианты одинаково модальны. Если две варианты имеют одинаковые частоты, то две моды свидетельствуют о бимодальном распределении. Часто бимодальные распределения указывают на качественную неоднородность совокупности по изучаемому признаку. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле  (5.21) (5.21)где XМо – нижняя граница модального интервала (модальный интервал определяется по наибольшей частоте); iМо – величина модального интервала; fMo, fMo–1, fMo+1 – частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно). По данным табл. 5.2 рассчитаем моду, тыс. руб.: 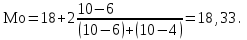 Итак, у наибольшего числа предприятий данной совокупности стоимость ОПФ составляет 18,33 тыс. руб. Медиана (Ме) – это варианта, которая находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы. Пусть ряд состоит из показателей заработной платы 9 рабочих (руб. в месяц ) в 2009 г.: 14600, 14800, 14950, 15600, 15700, 15950, 16700, 17200, 17550. Номер медианы для нечетного объема вычисляется по формуле 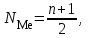 где n – число членов ряда. В нашем примере номер медианы равен 5, медиана равна 15700 руб. (т.е. половина рабочих получает зарплату 15700 руб. в месяц и более). В случае четного объема ряда медиана равна средней из двух вариант, находящихся в середине ряда. В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Медианным является первый интервал, в котором кумулятивная частота (накопленная сумма частот) равна или превышает половину общего числа наблюдений ( 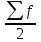 ). ).Значение медианы вычисляется по формуле 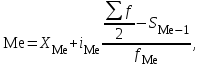 (5.22) (5.22)где XMe – нижняя граница медианного интервала; iMe – величина медианного интервала; 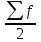 – половина от общего числа наблюдений; – половина от общего числа наблюдений;SMe–1 – кумулятивная частота в интервале, предшествующем медианному; fMe – число наблюдений в медианном интервале. Рассчитаем медиану по данным табл. 5.2. Прежде всего, найдем медианный интервал. Таким интервалом очевидно будет интервал стоимости ОПФ малых предприятий (18–20 тыс. руб.), поскольку его кумулятивная частота равна 18 (2+6+10), что превышает половину суммы всех частот (25:2 = 12,5). Нижняя граница интервала 18 млн руб., его частота 10; частота, накопленная до него, равна 8. Подставив данные в формулу (5.22), получим, тыс. руб.: 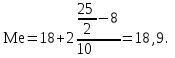 Полученный результат говорит о том, что половина предприятий региона имеет стоимость ОПФ 18,9 тыс. руб. и более. 6. ПОКАЗАТЕЛИ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЕТА Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, росту, весу, любимому занятию в свободное время и т.д. Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (например, о продолжительности жизни людей, доходах и расходах населения, финансовом положении предприятия и т.п.) для принятия научно-обоснованных управленческих решений. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней. Это можно показать на таком примере. Предположим, что одинаковую работу выполняют две бригады, каждая – из трех человек. Пусть количество деталей, шт., изготовленных за смену отдельными рабочими, составляло: - в первой бригаде – 95, 100, 105 (  = 100 шт.); = 100 шт.);- во второй бригаде – 75, 100, 125 ( 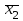 =100 шт.). =100 шт.). Средняя выработка на одного рабочего в обеих бригадах одинакова и составляет  = =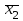 =100 шт., однако колеблемость выработки отдельных рабочих в первой бригаде значительно меньше, чем во второй. Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей. =100 шт., однако колеблемость выработки отдельных рабочих в первой бригаде значительно меньше, чем во второй. Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей. К показателям вариации относятся: размах вариации; дисперсия и среднее квадратическое отклонение; коэффициент вариации. Самым элементарным показателем вариации признака является размах вариации (R), представляющий собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: R = xmax– xmin . (6.1) В нашем примере размах вариации сменной выработки деталей составляет: в первой бригаде – R1 = 10 шт. (т.е. 105 – 95); во второй бригаде – R2= 50 шт. (т.е. 125 – 75), что а 5 раз больше. Это свидетельствует о том, что при численном равенстве средняя выработка первой бригады более «устойчива». Размах вариации может служить базой расчета возможных резервов роста выработки. Таких резервов больше у второй бригады, поскольку в случае достижения всеми рабочими максимальной для этой бригады выработки деталей, ею может быть изготовлено 375 шт., т.е. (3∙125), а в первой только 315 шт., т.е. (3∙105). Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. Чем больше размах вариации, тем вероятнее то, что средняя окажется нетипичной. Вторым показателем, характеризующим вариацию является дисперсия (σ2) признака. Дисперсию можно рассчитать обычным (прямым) способом. При таком расчете дисперсия представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): а) простая дисперсия для несгруппированных данных: 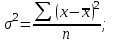 (6.2) (6.2)б) взвешенная дисперсия для сгруппированных данных: 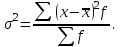 (6.3) (6.3)Дисперсия не имеет единицы измерения. В статистике она выступает только базой для расчета среднего квадратического отклонения. Дисперсия может быть рассчитана по преобразованной формуле как разность средней из квадратов вариант и квадрата их средней. 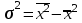 (6.4) (6.4)а) для несгруппированных данных: 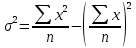 (6.5) (6.5)б) для сгруппированных данных: 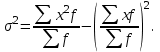 (6.6) (6.6)Техника вычисления дисперсии по формулам (6.2 – 6.6) достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике). Приведем два из них: 1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится; 2) если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз. Используя свойства дисперсии, получим формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов: 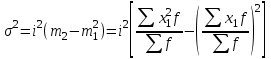 (6.7) (6.7)где σ2– дисперсия, исчисленная по способу моментов; i – величина интервала; 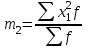 – момент второго порядка; – момент второго порядка;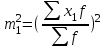 – квадрат момента первого порядка. – квадрат момента первого порядка.Расчет дисперсии по формуле (6.7) менее трудоемок. Среднее квадратическое отклонение ( 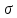 ) равно корню квадратному из дисперсии: ) равно корню квадратному из дисперсии: (6.8) (6.8)Среднее квадратическое отклонение ( 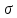 ) – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение имеет ту же единицу измерения, что и варианты х. ) – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Среднее квадратическое отклонение имеет ту же единицу измерения, что и варианты х.В статистической практике часто возникает необходимость сравнения вариаций различных признаков, например, вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях. Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации – коэффициент вариации. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической: 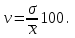 (6.9) (6.9)Средняя считается типичной и может служить обобщающей характеристикой совокупности единиц, если коэффициент вариации не превышает 33 %. Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||