Статья. Конечноэлементное моделирование многослойных ограждающих конструкций
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
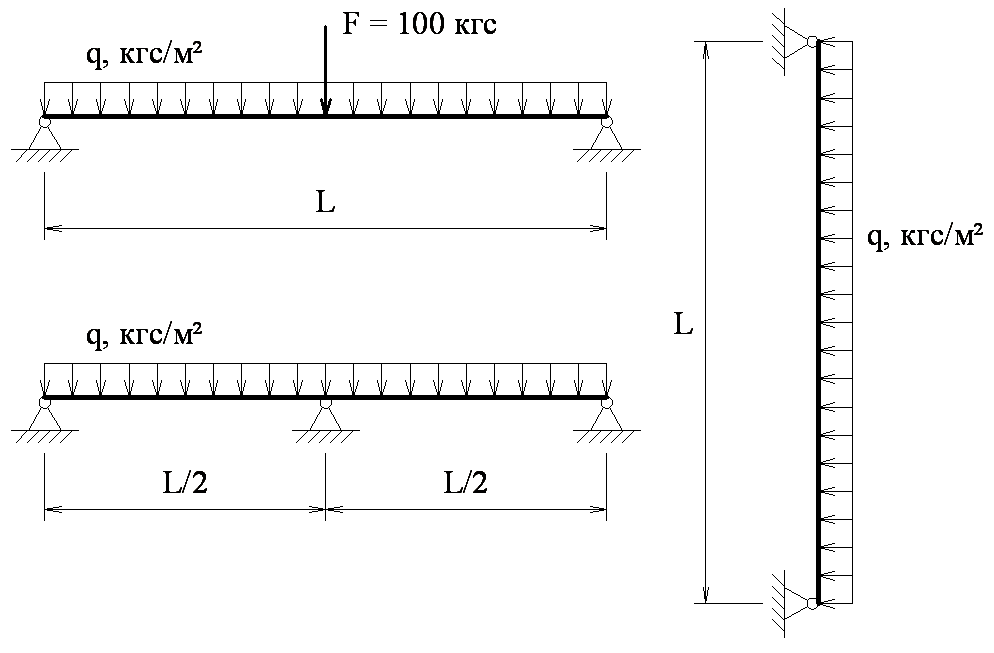
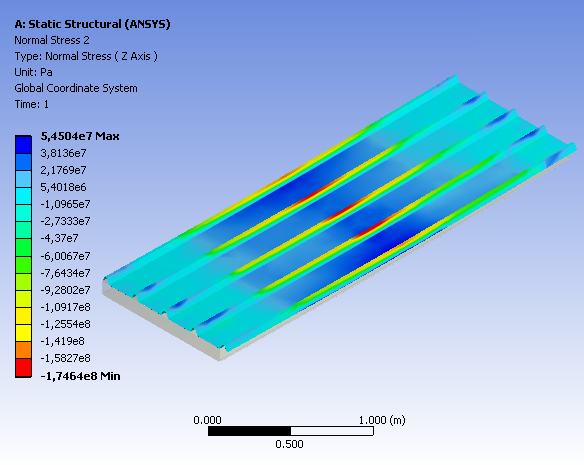
КОНЕЧНОЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ МНОГОСЛОЙНЫХ ОГРАЖДАЮЩИХ КОНСТРУКЦИЙ М.Н. Данилов Научный руководитель: д.т.н., проф. Н.Н. Федорова Новосибирский государственный архитектурно-строительный университет, г. Новосибирск, Россия Аннотация. В работе на основе численного моделирования в программном комплексе ANSYS определены поля напряжений и деформаций, а так же температурные поля в строительных сэндвич-панелях. Ключевые слова: сэндвич-панели, метод конечных элементов, ANSYS, напряженно-деформированное состояние, температурные поля. 1. Введение. Трехслойные строительные сэндвич-панели нашли в настоящее время широкое применение в строительстве. В отличие от достаточно изученного опыта использования таких панелей за рубежом, их эксплуатация в российских условиях имеет ряд особенностей. К ним относятся: большой перепад температур в течение года (от минус 40 в зимний период до плюс 40°С в летний); значительные снеговые нагрузки; длительность воздействия нагрузок, а также многократное повторение за время эксплуатации сооружения. Следует иметь в виду, что при производстве трехслойных панелей в России используются местные материалы, свойства которых отличаются от зарубежных аналогов, что также накладывает отпечаток на характер поведения ограждающих конструкций. Именно поэтому для обеспечения безопасной эксплуатации панелей требуются дополнительные исследования их поведения в условиях российского климата, а также производства. Специфика данного вида строительных изделий заключается в большом разнообразии возможных конструктивных решений и используемых для изготовления материалов. Вследствие этого зачастую возникают сложности при проведении расчетов, так как отсутствует достаточно простая, универсальная, предназначенная для широкого использования, методика расчета таких панелей, учитывающая особенности их работы в реальных условиях. Существующие методики проектирования и расчета многослойных ограждающих конструкций, используемые предприятиями, выпускающими сэндвич-панели, не отвечают современным требованиям и тенденциям, и не позволяют создавать конкурентоспособную продукцию. Данные методики требуют создания большого количества образцов и проведения испытаний на сложном дорогостоящем оборудовании, что связано со значительными материальными и временными затратами. Повышенные требования к прочности и надежности, а также к сопротивлению теплопередаче при уменьшении материалоемкости создают сложные проблемы анализа напряженно-деформированного состояния (НДС) и температурных полей данных конструкций. В связи с этим одной из главных задач является совершенствование методов расчета и проектированиясэндвич-панелей. Теоретические основы[1,2] уже вполне разработаны, и трудно ожидать принципиально новых открытий. Расчет многослойных систем методами теориитонких пластини оболочек сложен и далеко не всегда оправдан. Теории расчета балок и стержней, созданные и развитые целым рядом ученых, упрощают задачу, но возникают проблемы при расчете сложных несимметричных систем. Весьма эффективным оказывается использование численных методов. Необходимость разработки практической методики расчета совершенно очевидна. Решение этих вопросов в последнее время стало возможным благодаря широкому использованию средств вычислительной техники. Было получено много новых результатов, касающихся разработки алгоритмов решения задач по расчету многослойных конструкций численными методами на ЭВМ. Одним из универсальных методов является метод конечных элементов (МКЭ). МКЭ является синтезом энергетических методов, представлений о конечных разностях и структурном моделировании при помощи вычислительных машин. В расчетах многослойных конструкций со сложными моделями деформирования графическое представление о равновесном состоянии теряет свою наглядность и простоту, в то время как методы решений, основанные на вариационно-матричных постановках проявляют свои преимущества наиболее показательным образом и, пожалуй, становятся единственно пригодными. Очевидным решением является внедрение и применение специальных программных комплексов для ЭВМ, позволяющих значительно ускорить и удешевить процесс разработки и запуска в производство новых видов продукции. В настоящей работе для оптимизации прочностных и теплоизоляционных свойств строительных сэндвич-панелей использован программный комплекс ANSYS [3]. Основанный на методе конечных элементов программный комплекс позволяет проводить имитационное моделирование исследуемой конструкции. Все вышеизложенное говорит об актуальности рассматриваемой проблемы. Необходимо разработать методику расчета и рекомендовать конструктивные мероприятия, которые позволят эффективно увеличить несущую способность панелей, предотвратить возможную местную потерю устойчивости в обшивках, нарушение целостности слоя утеплителя и расслоение, а так же повысить теплозащитные их свойства. Статья посвящена исследованию работы элементов многослойных панелей, с применением методов численного анализа. Решаются задачи статики линейной теории упругости и стационарного теплового поля. Проведены исследования по выбору оптимальных геометрических параметров элементов панелей. Исследовано влияние геометрических параметров элементов панелей на величину критических нагрузок и порядок наступления предельных состояний. Выполнен расчет сопротивления теплопередаче ограждающей конструкции для различных толщин слоя утеплителя. Целью является дальнейшее развитие практической составляющей численных методов для решения задач линейного деформирования многослойных панелей и нахождения стационарного теплового поля. В работе разработаны практические методы расчета на нахождение НДС элементов многослойных конструкций, определения ее несущей способности и сопротивления теплопередаче с учетом всех конструктивных особенностей. Разработана методика расчета, соответствующая рекомендациям СНиП и которая может быть использована предприятиями и лабораториями. Научную новизну работы составляют заключения и выводы о влиянии формы сечения и геометрических размеров на пространственную устойчивость и несущую способность панелей. Представлены результаты в виде графиков, которые могут быть использованы для проверки несущей способности и сопротивления теплопередаче панелей. Достоверность результатов основывается на удовлетворительном согласовании теоретических и экспериментальных результатов[]. Теоретической и методической основой исследования послужили работы отечественных и зарубежных ученых []. В результате проведенных численных исследований определена практическая ценность: установлено влияние критической разрушающей нагрузки на приоритет наступления предельных состояний. Использование полученных результатов при новых расчетах позволяет придавать форму поперечного сечения, отличную от существующих, которая позволит повысить несущую способность. Основное положение работы - это рекомендации и методики по конечно-элементному моделированию процесса и результаты с практической составляющей при проектировании или усилении существующих многослойных конструкций. 2. Методика проведения вычислительного эксперимента. Объектом исследования являлись модели стеновых и кровельных трехслойных панелей со стальными профилированными обшивками и минераловатным средним слоем. Задача о напряженно-деформированном состоянии конструкции сэндвич-панели и задача нахождения температурных полей решались методом конечных элементов с помощью широко известного и хорошо зарекомендовавшего себя программного комплекса ANSYS. Расчетная модель создана в расчетной среде ANSYS Workbench. Приняты следующие основные допущения: 1) задача решается в статической постановке; 2) задача является симметричной; 3) слой утеплителя неразрывно соединен с обшивками с помощью клеевого соединения; ламели минеральной ваты в слое утеплителя могут контактно взаимодействовать друг с другом без трения; 4) материалы элементов конструкции линейно-упругие; материал среднего слоя ортотропный. Физико-механические свойства материалов взяты из справочников по свойствам материалов, а так же из опубликованных результатов лабораторных исследований проводимых предприятиями, выпускающими сэндвич-панели. 3D-модели конструкций создавались в двух приложениях: ANSYS DesignModeler и AutoCAD. Оба приложения допускают возможности создания параметрической модели. Параметризация позволила существенно сократить время на разработку геометрических моделей, так как для проведения исследований требовалось большое количество однотипных моделей, отличающихся по некоторым параметрам. Были назначены такие параметры, как: толщина слоя утеплителя, ширина панели, толщина обшивки, геометрические параметры «замкового» соединения, геометрические параметры профиля листа, толщина слоя клея, зазоры между слоями и др. Путем изменения числовых значений параметров вносились необходимые изменения в 3D-модель конструкции. Схема конструкции и расчетная сетка показаны на рисунке 1. 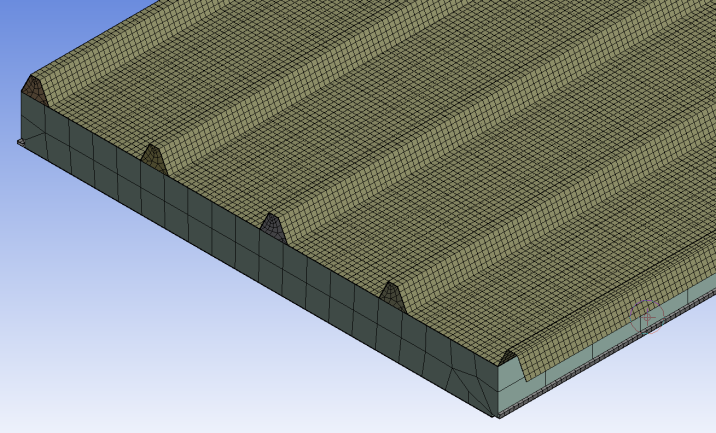 Рис. 1. Схема конструкции панели и расчетная сетка Обшивки панелей и слои клея смоделированы оболочками. Это позволило резко сократить количество конечных элементов с 1300000 до 450 000. При разбивке панели на конечные элементы был принят наиболее рациональный размер элемента (шаг сетки) из условия наименьшего количества элементов при обеспечении достаточной точности результатов. Шаг сетки на слое утеплителя выбран более крупным, чем на наружных обшивках. Такой выбор обусловлен большими размерами и простой геометрией среднего слоя, в отличие от обшивок, имеющих сложную геометрию (из-за профиля и замковых соединений) и малую толщину. 2.1. Задача о напряженно-деформированном состоянии. Для исследования напряженно-деформированного состояния панели использовался статический структурный анализ конструкции. Была принята следующая схема нагружения. Площадка опирания на прогон – минимум 50-60 мм; закрепление фиксированное во всех трех направлениях. Панель нагружалась по однопролетной и многопролетной схемам (Рис. 2). К панели были приложены следующие нагрузки: - сосредоточенная сила F = 100 кгс, приложенная по центру панели; по СНиП 2.01.07-85* Нагрузки и воздействия; - гравитация g = 9,81 м/с2; - равномерно распределенная нагрузка Q, кгс/м2, соответствующая наступлению предельного прогиба панели (L/200). В рамках исследования НДС панели были проведены исследования: - приоритетности параметров разрушения, влияющих на несущую способность панели и, соответственно, определение величины критической нагрузки при различных схемах работы; - характера распределения напряжений в элементах трехслойной конструкции; - характера перемещений; - влияния геометрических характеристик обшивок на НДС панели; - влияния толщины утеплителя на НДС панели; - влияния величины пролета на НДС панели; - влияния схемы работы панели (однопролетная, двухпролетная) на НДС панели; - расчет на устойчивость сжатой обшивки. В результате анализа панели был установлен характер распределения напряжений в элементах трехслойной конструкции (Рис. 3).
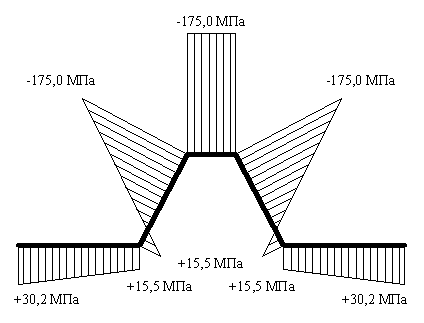
По длине панели напряжения распределены в виде стандартной эпюры. Наиболее нагруженными элементами гофрированной обшивки являются верхние полки гофров в середине пролета (Рис. 4, 5). Гофры сжаты только в центре панели, причем наиболее сжат средний гофр. В районе опор верхние полки гофров растянуты; в результате больших касательных и нормальных напряжений, возникающих на торце панели при больших прогибах, происходит расслоение. Нижние полки гофров растянуты. С увеличением высоты гофра увеличиваются напряжения в верхней полке гофрированной обшивки.
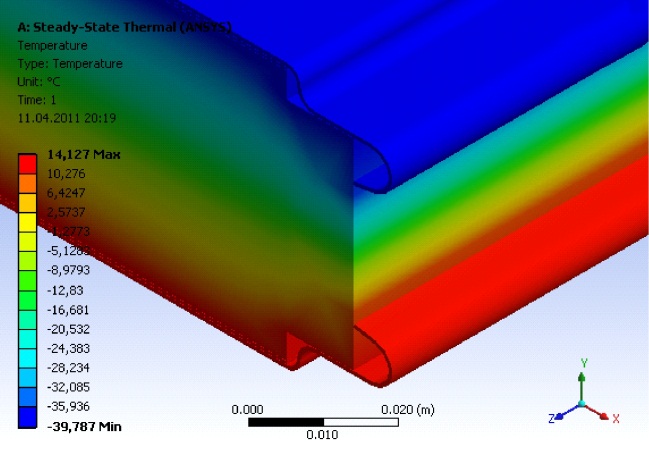
В пролете панели имеются скачки напряжений, связанные с разрезкой ламелей и составляют 1-3% по сравнению с напряжением в соседних элементах. При рассмотрении нижней обшивки панели было установлено, что обшивка по всей длине пролета растянута. Зависимость предельной нагрузки от длины панели и толщины слоя утеплителя приведена на рисунке 4. 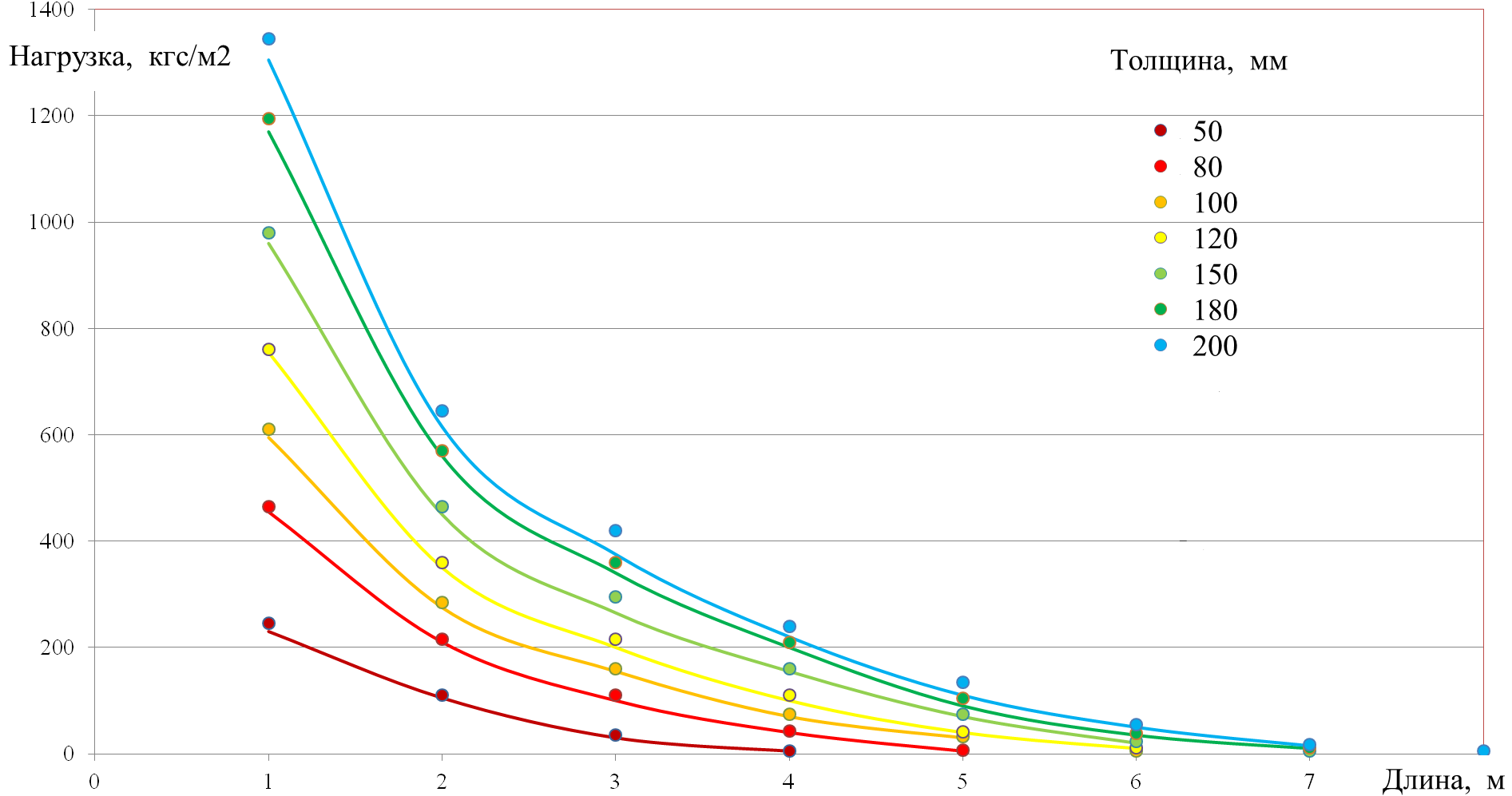 Рис. 6. Зависимость предельной нагрузки от длины панели и толщины слоя утеплителя; сравнение экспериментальных данных с расчетными 2.2. Тепловой анализ. Для проведения теплового анализа использовались расчетные модели стеновых сэндвич-панелей размерами 1000х1000 мм. Теплопроводность утеплителя принята 0,045 Вт/(м·ºC). На наружной поверхности панели задан конвективный теплообмен с температурой ‑42 ºC [2] и коэффициентом теплопередачи αн = 23,0 Вт/(м²·ºC). На внутренней поверхности панели также задан конвективный теплообмен с температурой +20 ºC и коэффициентом теплопередачи αв = 8,7 Вт/(м²·ºC). Таким образом создается тепловой поток проходящий через панель [3].
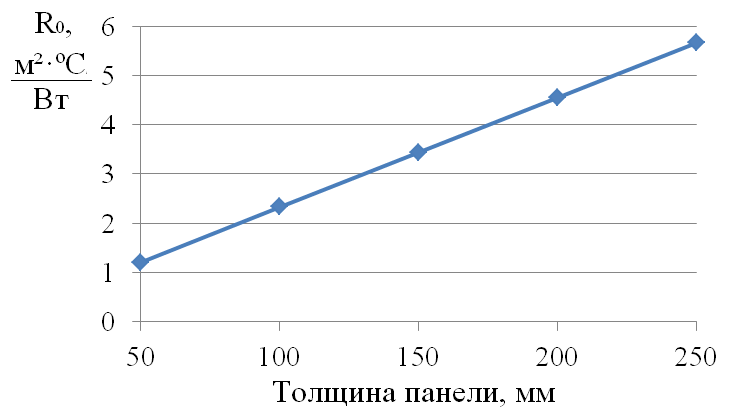
По величине теплового потока и значениям температур наружной и внутренней поверхностей было определено приведенное сопротивление теплопередаче панелей различной толщины h = 50250 мм (Таблица 1). Сопротивление теплопередаче ограждающей конструкции R0, м²·ºC/Вт: 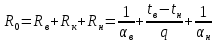 , ,где αн, αв – коэффициенты теплоотдачи, соответственно для наружной и внутренней поверхности, Вт/(м²·ºC); αв = 8,7 Вт/(м²·ºC); αн = 23,0 Вт/(м²·ºC); tн, tв – температуры наружной и внутренней поверхностей ограждающей конструкции, ºC; q – плотность теплового потока, Вт/м². Таблица 1. Результаты расчета тепловых потоков
По результатам анализа представленного поля температур можно сделать следующие выводы: 1. Разница между температурой внутренней поверхности стены в зоне соединительного ребра и температурой внутреннего воздуха составляет 2-6°С; предельно допустимое значение, указанное в [1] равное 4°С превышено только для панели с толщиной утеплителя 50 мм. 2. При температуре внутреннего воздуха 20°С и влажности 60% температура, при которой возможно выпадение конденсированной влаги (точка росы) составляет 12°С, а минимальная температура внутренней поверхности панели 14°С; таким образом намокание внутренней поверхности стены маловероятно. 3. Наличие замкового соединения оказывает не существенное влияние на распределение температуры в пределах рассматриваемого участка, что позволяет говорить о эффективности конструктивного решения замкового соединения. 4. Влияние замкового соединения сказывается на распределении температуры на поверхности стены, поэтому температурное поле стены не может быть с достаточной точностью оценено по одномерной схеме. 5. В зоне стыка распределение температуры по сечению в середине ребра близко к линейному, что характерно для сплошных стен, т.е. падение температуры наблюдается практически равномерно по всей толщине стены. 3.Выводы. Результаты численного моделирования и расчета строительных сэндвич-панелей показали следующее: 1. Программный комплекс ANSYS позволят производить корректное моделирование сложных неоднородных конструкций. 2. Результаты расчетов, выполненных в программном комплексе ANSYS, соответствуют теоретическим и экспериментальным данным с достаточной точностью. Сравнение результатов свидетельствует об их незначительных расхождениях – в пределах 10% (для прочностных и деформативных характеристик) и 5% (для теплоизоляционных характеристик). Это говорит о достоверности результатов, полученных на основе модели, разработанной на методе конечных элементов. Некоторое расхождение с экспериментальными данными объясняется тем, что в программе МКЭ расчет выполнялся без учета нелинейностей. 3. Разработана методика численного расчета конструкций на несущую способность и сопротивление теплопередаче с учетом всех конструктивных особенностей. 4. Даны практические рекомендации для конструирования новых типов поперечных сечений панелей. 5. При анализе результатов расчета тестовых задач на основе МКЭ было определено НДС панели. Установлено, что при однопролетной схеме работы в середине пролета внешний момент воспринимается обшивками, средний же слой при этом нагружен чрезвычайно слабо. При двухпролетной схеме в середине пролета момент воспринимается обшивками, а над средней опорой момент воспринимается гофрированной обшивкой и утеплителем. 6. Наличие замкового соединения в трехслойных стенах влияет на температурно-влажностный режим конструкции, в связи с чем расчет данной конструкции в одномерном пространстве является неточным. 7. Предложенная инженерная методика расчета трехслойных панелей с маложестким утеплителем и обшивками разной изгибной жесткости при однопролетной и многопролетной схемах работы. 8. Разработаны практические рекомендации по подбору панелей под заданную нагрузку и климатические условия. СПИСОК ЛИТЕРАТУРЫ 1. Александров А.Я., Брюккер Л.Э., Куршин A.M., Прусаков А.П. Расчет трехслойных панелей. - М.: Оборонгиз, 1960. 2. СНиП «Нагрузки и воздействия». 2. СНиП 23-01-99* Строительная климатология. 3. СП23-101-2004. Проектирование тепловой защиты зданий. 4. ГОСТ 26254-84 Здания и сооружения. Методы определения сопротивления теплопередаче ограждающих конструкций. 5. ГОСТ 21562-76 Панели металлические с утеплителем из пенопласта общие технические условия. 6. Каталог фирмы «Thermoland» Искитим, 2009. 7. http://www.ansys.com/ |