Исследовательская работа Магический квадрат. Исследование.Магический квадрат. Конкурс Малая академия
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
|
Муниципальное бюджетное общеобразовательное учреждение «Дуденевская школа» Конкурс «Малая академия» Номинация «Математический калейдоскоп» Магический квадрат – волшебный помощник в счете Выполнили: Клак Сергей Александрович, Челышева Дарья Дмитриевна, Чистов Никита Алексеевич, учащиеся 3 класса. Научный руководитель: Морковкина Любовь Геннадьевна, учитель начальных классов с. Дуденево 2015 г. Содержание 1. Введение…………………………………………………………………. 3 2. Основная часть 2.1. История появления магических квадратов…………………………....4 2.2. Виды магических квадратов…………………………………………....6 2.3. Правила построения магических квадратов…………………………..8 2.4. Практическая часть…………………………………………………….10 3. Заключение……………………………………………………………….12 4. Список литературы………………………………………………………13 5. Приложения………………………………………………………………14 Введение «В дни моей юности я в свободное время развлекался тем, что составлял… магические квадраты» Бенджамин Франклин. На уроке математики мы часто выполняем задания на скорость счета. Кто быстрее решит 10 примеров, 5 простых задач, разгадает магический квадрат. Учитель сказал нам, что в 4 классе мы будем сдавать экзамен на скорость счета. Решать устно не так просто! У нас не всегда получается считать быстро и правильно. Нам очень нравится разгадывать магические квадраты. Но перебирая цифры при их составлении, мы тратим много времени. Мы решили заняться исследованием, чтобы раскрыть «секреты» быстрого разгадывания магических квадратов. Думаем, что такая работа поможет нам научиться быстрому счету. Объект исследования: магический квадрат. Цель исследования: раскрыть «секреты» магического квадрата для улучшения скорости счета. Задачи исследования: Познакомиться с историей появления магических квадратов. Изучить способы составления магических квадратов. Научиться составлять магические квадраты. Провести соревнование с учащимися 4 класса по разгадыванию магических квадратов. Гипотеза: предположим, что составляя свои магические квадраты, мы научимся лучше считать. Методы исследования: наблюдение; анализ научной литературы; анкетирование учащихся, анализ, сравнение и обобщение результатов; 2.1. История появления магических квадратов Магические квадраты.… От этого словосочетания сразу веет волшебством. Великие ученые древности считали, что числа имеют какую-то самостоятельную жизнь, свои тайны. Существовало поверье, что выбитый на серебре магический квадрат защищает от чумы. На востоке его использовали при заклинаниях. Даже сегодня среди европейских прорицателей можно увидеть магические квадраты. Что же такое магический квадрат? Магический или волшебный квадрат – это квадратная таблица, заполненная числами так, что сумма чисел в каждой строке, каждом столбике и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Существует предание, согласно которому китайский император Ию, примерно 4000 лет тому назад, увидел на берегу реки священную черепаху с узором из черных и белых кружков на панцире (см. приложение 1). Если посчитать количество кружочков в каждой фигуре, и поместить полученные числа в клетки квадрата, получится магический квадрат. Если сложить числа любой строки, то получится 15. 4+9+2=15, 3+5+7=15, 8+1+6=15 При сложении любого столбца тоже получается 15. 4+3+8=15, 9=5=1=15, 2+7+6=15 Тот же результат получается при сложении чисел по диагоналям: 4+5+6=15, 8+5+2=15 В XI веке о магических квадратах узнали в Индии, а затем в Японии. Европейцы познакомились с магическими квадратами в XV веке. Первым квадратом, придуманным европейцем, считается квадрат великого знаменитого художника Альбрехта Дюрера, изображенный на его гравюре «Меланхолия» (см. приложение 2). Этот квадрат составлен из чисел, записанных арабскими цифрами. Интересно, что средние числа в нижней его строке изображают год создания гравюры – 1514. Возможно, Дюрер знал этот квадрат, а может быть, начав именно с этих чисел, смог найти остальные методом подбора. Магическая сумма его равна 34. При сложении чисел любой строки получается 34. 16+3+2+13=34, 5+10+11+8=34, 9+6+7+12=34, 4+15+14+1=34 При сложении чисел любого столбца получается 34. 16+5+9+4=34, 3+10+6+15=34, 2+11+7+14=34, 13+8+12+1=34 Тот же результат получается при сложении чисел по диагоналям. 16+10+7+1=34, 13+11+6+4=34 Квадрат Дюрера обладает и другими свойствами, не такими, как остальные магические квадраты. Сумма чисел каждого из угловых квадратов и сумма чисел центрального квадрата одинакова. Она тоже равна 34. 16+3+5+10=34, 2+13+11+8=34, 9+6+4+15=34, 7+12+14+1=34, 10+11+6+7=34 Построение магических квадратов – старинное развлечение. В далекие времена их построение было серьезным исследованием. В XVI веке математическая теория построения магических квадратов была развита во Франции. Позднее ею заинтересовались авторы из разных стран. Составление магических квадратов – одна из самых интересных математических головоломок. Мы, третьеклассники, тоже заинтересовались этой темой. 2.2. Виды магических квадратов Полного описания всех возможных магических квадратов не получено и до настоящего времени. Квадратов 2X2 не существует, а 3X3 – единственный. Так как все остальные получаются из него либо поворотом вокруг центра, либо отражение одной из его осей симметрии. С увеличением числа клеток квадрата растет количество возможных магических квадратов. Различных квадратов 4X4 уже 880, а 5X5 приближается к четверти миллиона. Среди них есть очень интересные квадраты. В одном из них (см. приложение 3) равны между собой не только суммы чисел в строках, столбцах и диагоналей, но и суммы пятерок чисел по «разломанным» диагоналям, связанным на рисунке цветными линиями. Суммы в строках: 1+15+24+8+17=65, 9+18+2+11+25=65, 12+21+10+19+3=65, 20+4+13+22+6=65, 23+7+16+5+14=65. Суммы в столбцах: 1+9+12+20+23=65, 15+18+21+4+7=65, 24+2+10+13+16-65, 8+11+19+22+5=65, 17+25+3+6+14=65. Суммы в диагоналях: 1+18+10+22+14=65, 17+11+10+4+23=65. Суммы по «разломанным» диагоналям: 17+5+13+21+9=65, 8+25+16+4+12=65, 24+11+3+7+20=65, 15+2+19+6+23=65. 1+25+19+13+7=65, 9+15+3+22+16=65, 12+18+24+6+5=65, 20+21+2+8+14=65. Китайский математик Ян Хуэй в XIII веке сумел построить магический квадрат 6X6 (см. приложение 4). Сумма чисел в строках, столбцах и диагоналях равна 111. В строках: 27+29+2+4+13+36=111, 9+11+20+22+31+18=111, 32+25+7+3+21+23=111, 14+16+34+30+12+5=111, 28+6+15+17+26+19=111 1+24+33+35+8+10=111 В столбцах: 27+9+32+14+28+1=111, 29+11+25+16+6+24=111, 2+20+7+34+15+33-111, 4+22+3+30+17+35=111, 13+31+21+12+26+8=111, 36+18+23+5+19+10=111. В диагоналях: 27+11+7+30+26+10=111, 36+31+3+34+6+1=111. Интересен этот квадрат тем, что центрально противолежащие числа дают сумму 37 (кроме 2 пар, они отмечены подчеркиванием). Самый большой магический квадрат 12X12 построен в 1913 году Дж. Н.Манси. Он заполнен 144-мя нечетными числами (исключение составляет число 2). Его магическая сумма составляет 4514 (см. приложение 5). 2.3. Правила построения магических квадратов Существует несколько способов составления магического квадрата. Мы решили остановиться на доступных для нас квадратах 3X3. Составление магического квадрата для последовательных чисел Записать в квадрат 9 последовательных чисел: 11 12 13 14 15 16 17 18 19 2) Поменять местами цифры, стоящие на противоположных концах диагоналей: 11 и 19, 13 и 17: 19 12 17 14 15 16 13 18 11 3) Сдвинуть на шаг по часовой стрелке каждое из чисел: 14 19 12 13 15 17 18 11 16 Таким образом, мы получили магический квадрат, сумма которого (в любой строке, в любом столбце и на каждой из диагоналей) равна 45. 4) Из заполненного магического квадрата можно получить новый квадрат: увеличением всех чисел на одно и то же число, например, +3 17 22 15 16 18 20 21 14 19 о   тражением относительно осей симметрии: тражением относительно осей симметрии:17 22 15 15 22 17 15 22 17 15 20 19 16 18 20 20 18 16 20 18 16 22 18 14 21 14 19 19 14 21 19 14 21 17 16 21 Составление магического квадрата из произвольных чисел 1) Выбрать произвольных три числа. 2) Найти сумму этих трех чисел (магическая сумма) 3) Магическую сумму разделить на 3. Это число записывается в центре на пересечении диагоналей квадрата. При составлении квадрата нужно соблюдать два условия: - сумма трех произвольно взятых чисел должна делиться на 3 без остатка; - если разность наибольшего и наименьшего из трех выбранных чисел больше магической суммы, то следует расположить их на соседних клетках квадрата. Например, возьмем числа 3,9,12. Первое условие: (3+9+12):3=8. Второе условие: 12-3>8. Получаем магические квадраты: 12 9 9 3 12 14 8 2 11 8 5 7 4 13 4 13 7 Теперь мы готовы к самостоятельному составлению магических квадратов! Можно посоревноваться в их решении с ребятами из других классов. 2.4. Практическая часть Перед самостоятельным составлением магических квадратов мы решили проверить скорость счета своих одноклассников. Учительница предложила нам за 1 минуту решить несколько примеров на умножение. (см. приложение 6). Результаты оказались невысокими и представлены на диаграмме (см. приложение 7). В классе 8 человек, из них: 1 человек (12%) – высокий уровень; 1 человек (12%) – выше среднего; 1 человек (12%) – средний уровень; 5 человек (64%) – низкий уровень. Анализируя результаты проверки скорости счета, можно сделать вывод, что третьеклассники считают очень медленно. В настоящее время учащиеся школы мало решают математические головоломки, ребусы, кроссворды. Для того, чтобы выяснить, знают ли современные школьники, что такое магический квадрат, мы провели анкетирование. Было опрошено 20 учащихся из 2 и 4 классов. На вопрос: знаете ли вы, что такое магический квадрат, 30% учащихся ответили «да», 70% - «нет». На вопрос: решая магические квадраты, ты научишься быстрее считать, 30% ребят ответили «да», 20% - «нет», 50% - сомневаюсь. На вопрос: хотели бы вы посоревноваться с третьеклассниками в решении магических квадратов, 70% учеников ответили «да», 30% - «нет». Результаты анкетирования представлены в виде диаграмм (см. приложение 8). 30 ноября 2015 года мы отправились на классный час к четвероклассникам. Рассказали им про магический квадрат, научили строить свои квадраты и предложили посоревноваться в их решении. И ровно через неделю состоялся конкурс «Кто быстрее решит магический квадрат» (см. приложение 9). Счет в конкурсе 4: 4! Мы были рады. Значит, магический квадрат действительно волшебный помощник в счете! Целый месяц мы составляли свои магические квадраты и разгадывали их на уроках математики, в группе продленного дня, после уроков с одноклассниками. За это время мы создали целую копилку квадратов! Недавно учитель снова проверял у нас скорость счета. Результаты следующие: 2 человека (25%) – высокий уровень; 1 человек (12%) – выше среднего; 3 человек (38%) – средний уровень; 2 человек (25%) – низкий уровень. Да, мы стали считать лучше! Это видно из диаграммы (Приложение 10).  Заключение Работа над данной темой позволила нам познакомиться с понятием магического квадрата, его историей, видами и свойствами, помогла узнать способы их построения. Решение таких задач не только доставляет удовольствие тем, кто интересуется математикой, но и служит прекрасной «гимнастикой для ума». В этом мы убедились сами. Собрав огромную копилку квадратов (см. приложение 11), мы стали считать лучше и быстрее. Наша гипотеза подтвердилась. Магический квадрат – это символ числовой гармонии. Он таит в себе ещё много загадок. Остаётся неизвестным общий метод построения всех магических квадратов. Мы думаем не останавливаться на полученных знаниях, а дальше изучать и строить математические квадраты! В период работы над исследованием было проведено анкетирование среди учащихся 2 и 4 классов. Мы не только сами заинтересовались магическими квадратами, но смогли увлечь этим занятием и других ребят. Материал, представленный в работе, выходит за рамки школьной программы, является прекрасным дополнением к разделу логических задач. Рекомендуем всем, кто увлекается математикой, кто желает знать больше, строить и решать магические квадраты. 4. Список литературы 1. Макарова Н.В. Волшебный мир магических квадратов. - Саратов, 2009. – 180 с. 2. Математика. Школьная энциклопедия / гл. ред. С.М. Никольский –М.: Большая российская энциклопедия; Дрофа, 1997. –527 с. 3. Трошин В.В. Магия чисел и фигур. – М.: Глобус, 2007 – 382 с. 4. Шуба М.Ю. Занимательные задания в обучении математике. – Москва: «Просвещение», 1996. – 182 с. 5. Энциклопедический словарь юного математика/ сост. А.П. Савин-3-е изд. М., Педагогика –Пресс, 1999. –360 с. 6. Я познаю мир: Детская энциклопедия: Математика / Сост. А.П. Савин и др. – М.: АСТ, 1996. – 480 с. 7. http://cad.narod.ru/methods/cadsystems/software/kvadrat/html Приложение 1 Cвященная черепаха 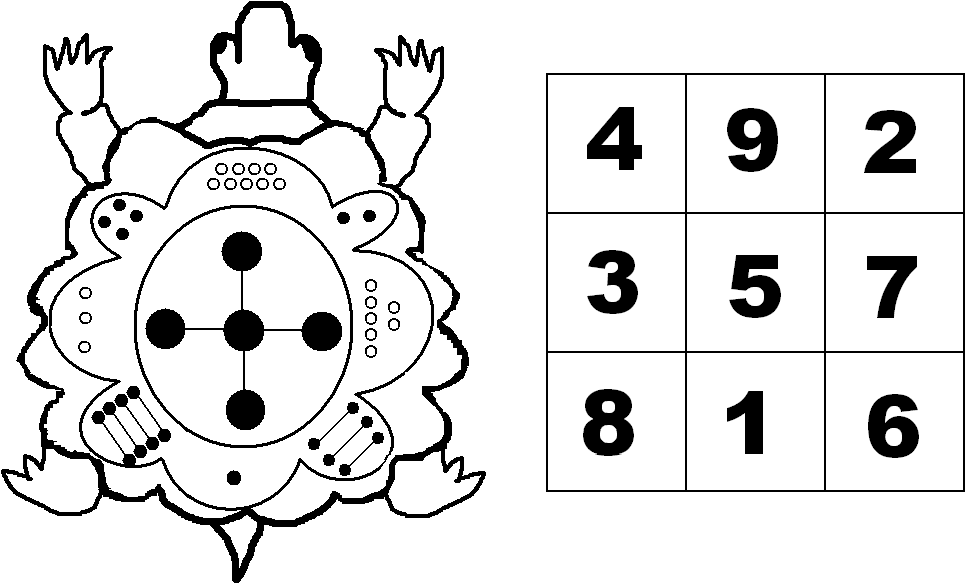 Китайский император Ию, примерно 4000 лет тому назад, увидел на берегу реки священную черепаху с узором из черных и белых кружков на панцире. Если посчитать количество кружочков в каждой фигуре, и поместить полученные числа в клетки квадрата, получится магический квадрат. Приложение 2 А.Дюрер «Меланхолия» Гравюра на меди. 1514 г.  Вот он знаменитый квадрат Дюрера  Приложение 3 Интересный магический квадрат 5x5 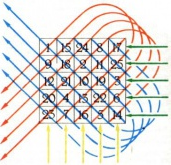 В этом магическом квадрате равны между собой не только суммы чисел в строках, столбцах и диагоналей, но и суммы пятерок чисел по «разломанным» диагоналям, связанным на рисунке цветными линиями. Приложение 4 Китайский математик Ян Хуэй в XIII веке сумел построить магический квадрат 6X6
Приложение 5 Самый большой магический квадрат 12X12
Приложение 6 Примеры для проверки скорости счета
Приложение 7 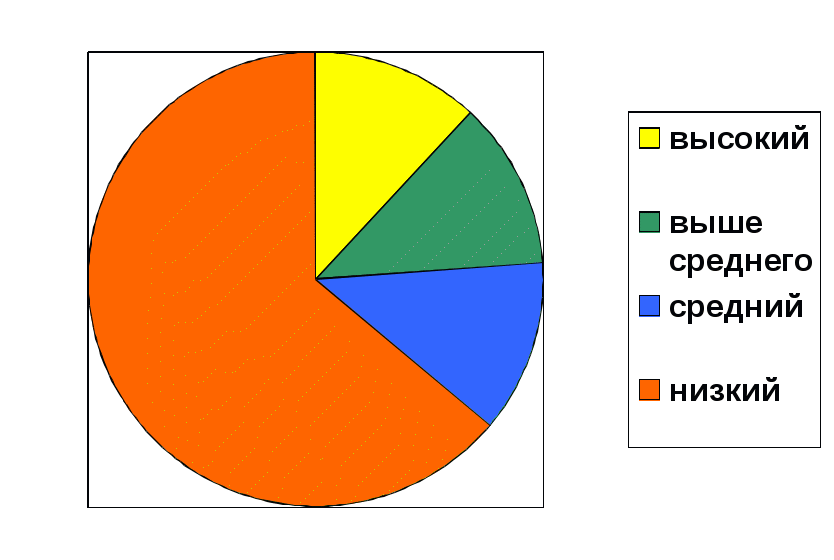 Первые результаты проверки скорости счета Результаты оказались невысокими. В классе 8 человек, из них: 1 человек (12%) – высокий уровень; 1 человек (12%) – выше среднего; 1 человек (12%) – средний уровень; 5 человек (64%) – низкий уровень. Интерпретация результатов при изучении скорости вычислений
Приложение 8 Результаты анкетирования  На вопрос: знаете ли вы, что такое магический квадрат, 30% учащихся ответили «да», 70% - «нет». На вопрос: решая магические квадраты, ты научишься быстрее считать, 30% ребят ответили «да», 20% - «нет», 50% - сомневаюсь. На вопрос: хотели бы вы посоревноваться с третьеклассниками в решении магических квадратов, 70% учеников ответили «да», 30% - «нет». Приложение 9 Конкурс «Кто быстрее решит магический квадрат»  Команда четвероклассников  Команда третьеклассников Приложение 10 Результаты скорости счета в конце исследования 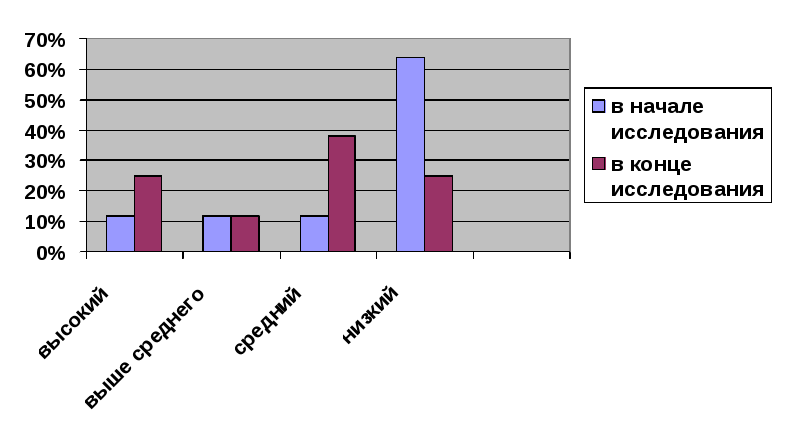 Высокий уровень: в начале – 12%, в конце – 25%. Выше среднего: в начале – 12%, в конце – 12%. Средний уровень: в начале – 12%, в конце – 38%. Низкий уровень: в начале – 64%, в конце – 25% Приложение 11 Копилка квадратов
Это только часть наших квадратов! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
