Ээс. Конспект лекций по дисциплине Экономикоматематические методы и модели для студентов специальности Экономика и организация производства

• Название: Конспект лекций по дисциплине Экономикоматематические методы и модели для студентов специальности Экономика и организация производства
• Дата: 08.06.2022
• Размер: 4.59 Mb.
• Имя файла: emmim.doc
• Тип: Конспект; #579709
• страница: 2 из 3

Параметры, используемые в экономико-математических методах и моделях.

Содержанием любой экономико-математической модели является выраженная в формально-математических соотношениях экономическая сущность условий задачи и поставленной цели. В модели экономическая величина представляется математическим соотношением, но не всегда математическое соотношение является экономическим.

Описание экономических условий математическими соотношениями – результат того, что модель устанавливает связи и зависимости между экономическими параметрами или величинами. Наиболее полное законченное определение экономико-математической модели дал академик В. С. Немчинов: "Экономико-математическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме".

По содержанию различают экономико-математические и экономико-

статистические модели. Различие между ними состоит в характере функциональных зависимостей, связывающих их величины. Так, экономико-статистические модели связаны с показателями, сгруппированными различными способами. Статистические модели устанавливают зависимость между показателями и определяющими их факторами в виде линейной и нелинейной функции. Экономико-математические модели включают в себя систему ограничений, целевую функцию.

Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами.

Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т. д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция – функция многих переменных величин и может иметь свободный член.

8. 
   Экономико-математические модели управления запасами. Однономенклатурные модели.
   

Теория управления запасами объединяет в себе методы анализа задач регулирования запасов некоторого продукта при независимом спросе на этот продукт.

В задачах такого рода необходимо найти рациональное количество запаса, учитывая, что потери возникают как из-за неудовлетворенного спроса, так и из-за того, что продукт хранится на складе.

Проблема управления запасами возникает при рассмотрении разнообразных экономических объектов. Широко распространены задачи управления запасами при анализе розничной торговли. В этом случае рассматриваются запасы некоторого продукта в магазине. Обычно спрос считается случайной величиной с заданным распределением. Запас пополняется за счет доставки товара с оптовой базы по заявке магазина, причем время доставки может быть фиксированным или же является случайной величиной.

Управление запасами заключается в установлении моментов и объемов заказов на их восполнение.

Совокупность правил, по которым принимаются такие решения, называется стратегией (системой) управления запасами.

Оптимальной стратегией считается та, которая обеспечивает минимум затрат по доведению продукции до потребителей.

Нахождение оптимальных стратегий составляет предмет теории оптимального управления запасами.

Эффективность работы склада оценивается по его затратам на пополнение запасов и их хранение. Работа реального склада сопровождается множеством отклонений от идеального режима, но для составления простейшей однопродуктовой статической модели управления запасами делаются следующие предположения:

- скорость расходования запасов со склада (спрос) является постоянной величиной, обозначим ее v (единиц товарных запасов в единицу времени),

- объем поступающей партии q является постоянной величиной,

- интервал времени между двумя поставки τ (цикл) является постоянным, дефицит недопустим,

- запас пополняется мгновенно от 0 до величины .

Динамика изменения уровня запаса на складе имеет вид, представленный на рис.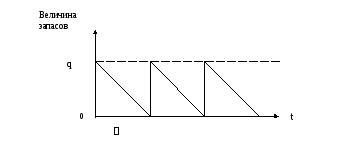



Рис. - График пополнения запаса идеального склада.

Обоснуем формулу для определения оптимального размера партии заказа, который обеспечивает минимум затрат.

Введем обозначения:

К ¬ затраты, не зависящие от объема партии,

S ¬ затраты на хранение одной единицы запасов в течение одной единицы времени.

Издержки хранения запасов будем считать пропорциональными величине хранящихся запасов и времени их хранения. Величина среднего размера запасов за время τ равна .

Таким образом, суммарные затраты за время τ при размере партии равны:



Учитывая, что , величина затрат на пополнение и хранение запасов в единицу времени равна:



Это выражение является целевой функцией, минимизация которой позволяет определить оптимальные режим работы склада. Так, оптимальный размер партии, при котором обеспечивается минимум затрат на пополнение и хранение запаса, можно определить методами дифференциального исчисления:

,

откуда оптимальный размер партии:

.

Эта формула называется формулой Уилсона по имени английского ученого-экономиста, который ее вывел в 20-х годах XX столетия.

Используя формулу Уилсона можно определить ряд расчетных характеристик работы идеального склада в оптимальном режиме:

оптимальная периодичность пополнения запасов

,

минимальные суммарные затраты на управление запасами в единицу времени

9. 
   Экономико-математические модели управления запасами. Модель с конечной интенсивностью поступления заказа.
   

Любая стратегия регулирования запасов призвана отвечать на два основных вопроса: когда заказывать очередную партию продукции, и сколько товара заказать?

Выделяют две основные стратегии регулирования запасов:

1) система с фиксированным размером заказа;

2) система с фиксированной периодичностью заказа.

Система с фиксированной периодичностью заказа. В данном случае продукция заказывается через равные промежутки времени, а размер запаса регулируется за счет изменения объема партии. Объем партии принимается равным разности между фиксированным максимальным уровнем, до которого производится пополнение запаса, и фактическим его размером в момент заказа.

Ситуацию иллюстрирует рисунок . На рисунке обозначены:

Max –максимальный (плановый) уровень;

l – интервал между заказами (планируемый период).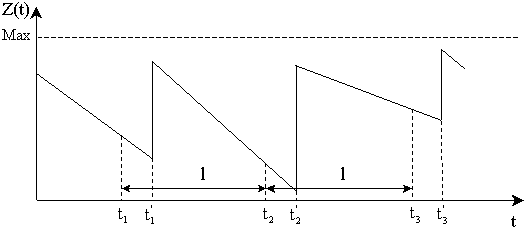


Рисунок – Движение запаса продукции при использовании стратегии с фиксированной периодичностью заказа

Регулируемыми параметрами в такой системе являются: максимальный (плановый) уровень (Max) и интервал времени между двумя заказами l, называемый также планируемым периодом).

Достоинство такой системы - отсутствие необходимости регулярного учета материалов. Недостатки: иногда приходится делать заказ на незначительное количество продукции, а при непредвиденно интенсивном потреблении возможно исчерпание запаса до наступления очередного момента заказа.

10. 
    Модель с учетом неудовлетворенных требований.
    

В общем случае, когда потери от дефицита сопоставимы с расходами по содержанию запасов, дефицит допустим.

График движения запаса для такой ситуации приведен на рисунке , где 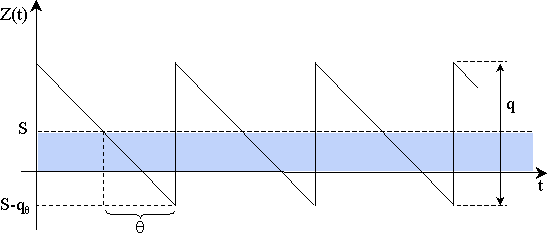  обозначает количество продукции, потребляемой в течение заготовительного периода.


Рисунок – Движение запаса в однопродуктовой статической модели, допускающей дефицит

Не производя подробного вывода формул, скажем следующее.

В случае, когда вид минимизируемой функции определяется посредством соотношений), оптимальные значения параметров q^* и S^*имеют следующий вид:




Нетрудно заметить, что при больших издержках от неудовлетворенного спроса, т.е. при недопустимости дефицита (a → ∞), q^* и S^* в формулах стремятся к соответствующим значениям q и S.

11. 
    Алгоритм Беллмана-Форда при при определении кратчайших расстояний на полигоне.
    

Кратчайшие пути находим с использованием алгоритма Форда. Каждой дуге данной сети отнесем число , которое назовем длиной дуги . Требуется найти путь из вершины в вершину , чтобы полная длина его была наименьшей, т.е. .

Процесс решения для сетей с большим числом вершин следующий:

1. Помечаем каждую вершину индексом ; первоначально берем и при .

2. Ищем такую дугу , для которой , затем заменяем индекс индексом . Заметим, что при . Процесс продолжается до тех пор, пока найдется хотя бы одна дуга, для которой можно уменьшить .

3. После того как индексы будут установлены, найдется такая вершина , для которой , так как индекс монотонно уменьшается и - последняя вершина, поступившая для его уменьшения. Точно также найдется вершина , для которой и так далее. Так как последовательность … строго убывающая, то при некотором получим и длину кратчайшего пути из в , .

С помощью алгоритма Форда можно получить кратчайшие пути только от одного узла. Затем необходимо переходить ко второму и так далее до тех пор, пока не будет известна вся матрица длин кратчайших путей. Матричная модификация алгоритма позволяет получить всю матрицу кратчайших путей.

Алгоритм поиска кратчайших путей между любыми двумя узлами сети основан на применении так называемой тернарной операции:

, если (11)

где - длина некоторой цепи, соединяющей -й и -й узлы;

- длины цепей, соединяющих соответственно -й , -й и -й узлы.

12. 
    Транспортная задача. Общая постановка, цели и задачи.
    

Частным случаем задачи линейного программирования является транспортная задача. 

ТЗ в общем виде состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А₁ , А₂ , ..., А_m в n пунктов назначения B₁ , B₂ , ..., B_n. В качестве критерия оптимальности можно взять минимальную стоимость перевозок всего груза, либо минимальное время его доставки. 

Рассмотрим задачу с первым критерием, обозначив через сn тарифы перевозок единицы груза из i-го пункта отправления в j-й пункт назначения, через a_i - запасы груза в пункте А_i через b_j - потребности в грузе пункта B_j ,x_ij - количество единиц груза, перевозимого из i-го пункта в j-й пункт. 

Составим математическую модель задачи. Так как от i-гo поставщика к j-му потребителю запланировано к перевозке x_ij единиц груза.

Соответственно математическая постановка задачи состоит в определении минимума целевой функции