Ээс. Конспект лекций по дисциплине Экономикоматематические методы и модели для студентов специальности Экономика и организация производства

• Название: Конспект лекций по дисциплине Экономикоматематические методы и модели для студентов специальности Экономика и организация производства
• Дата: 08.06.2022
• Размер: 4.59 Mb.
• Имя файла: emmim.doc
• Тип: Конспект; #579709
• страница: 3 из 3

Основные типы и виды моделей транспортной задачи.

Всякое неотрицательное решение систем уравнений (1)-(3),

	(i = l, ..., m),	(1)
	(j = 1, ..., n),	(2)
xij ≥ 0	(i = l, ..., m; j = l, ..., n).	(3)

определяемое матрицей X=(x_ij ), называют опорным планом ТЗ, а план X*=(x_ij ), при котором функция Z принимает минимальное значение – называется оптимальным планом ТЗ. 

Все данные, а затем и опорный план, удобно занести в распределительную таблицу. 

Если общее количество груза в пунктах отправления и общая потребность в нем в пунктах назначения совпадают, т.е.

(4)

то модель ТЗ называется закрытой; в противном случае – открытой. Для открытой модели может быть два случая: а) суммарные запасы превышают суммарные потребности:   ; б) суммарные потребности превышают суммарные запасы:   .

14. 
    Методы решения транспортной задачи. Метод минимального элемента.
    

Решение транспортной задачи, после того, когда было установлено, что она открытая либо устранен путем коррекции несбалансированность ее, начинается с составления опорного плана, то есть отыскания начального базисного решения.

Существует большой выбор методов составления опорного плана, рассмотрим некоторые из них.

Метод минимального элемента. Алгоритм метода минимального элемента состоит в следующем. Просматривается вся матрица тарифов перевозок, и из нее выбирается позиция с наименьшим значением тарифа C, затем просматриваются значения наличия запасов на складе A и потребности у потребителя B, затем в данную клетку записывается величина D=MIN(A,B). Из запасов соответствующего склада и потребностей магазина вычитается величина D. Если запас товара на складе исчерпан, то эта строка исключается из дальнейшего рассмотрения. Если потребность магазина в товаре удовлетворена полностью, то этот столбец исключается из дальнейшего рассмотрения. Может быть случай, когда одновременно исключаются и строка и столбец, этот случай называется вырожденным. В дальнейшем весь процесс повторяется до тех пор, пока не будет исчерпан весь запас товаров на складах и не будет удовлетворена потребность всех магазинов.

15. 
    Методы решения транспортной задачи. Метод наименьшей стоимости.
    

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj . Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены

16. 
    Методы решения транспортной задачи. Метод аппроксимации Фогеля.
    

Просматриваются все строки и столбцы матрицы тарифов, вычисляется разность между двумя наименьшими элементами в строке или в столбце. Затем из всех этих разностей выбирается строка или столбец с максимальной разностью. В выбранной строке или столбце, как и в методе минимального элемента, заполняется клетка с наименьшим значением тарифа. Затем обнулявшаяся строка или столбец исключаются из рассмотрения и весь процесс повторяется до полного исчерпания запаса товаров на складах.

17. 
    Методы решения транспортной задачи. Метод потенциалов.
    

Пусть одним из рассмотренных в теме (6) методов найден опорный план, содержащий n + m - 1 занятых клеток (в некоторых из них могут стоять нули). Поставим в соответствие каждому пункту отправления А_iнекоторое число u_i (i = l, ..., m) и каждому пункту назначения B_j - число v_j (j = 1, ..., n). Эти числа назовем потенциалами, соответственно, пунктов отправления и пунктов назначения.

Вопрос об оптимальности опорного плана решает следующая теорема:

Теорема. Если для некоторого плана X*= (x_ij ), (i = l, ..., m; j = l, ..., n) транспортной задачи выполняются условия:

1. u_i + v_j = c_ij для x_ij > 0 (для занятых клеток),  (1)

2. u_i + v_j < c_ij для x_ij = 0 (для свободных клеток),  (2)

то план X* является оптимальным. Из теоремы следует, что если для некоторой свободной клетки 
u_i + v_j < c_ij , то план не является оптимальным.

Отметим, что система (1) (m + n - 1) уравнений содержит (m + n) неизвестных u_i , v_j , и потому, приравнивая одно из них, например u₁ к нулю, однозначно определим остальные неизвестные.

Для «улучшения» опорного плана (при невыполнении условия (2) выбирают свободную клетку с max (u_i + v_j - c_ij ) и строят для нее цикл пересчета (сдвига).

18. 
    Методы решения транспортной задачи. Диагональный метод.
    

Метод северо-западного угла наиболее прост, так базисное решение получается путем последовательного перехода по столбцам и строкам. Кроме этого стоит учитывать, что алгоритм выбора начального базисного решения не влияет на алгоритм поиска оптимального решения, то есть в любом случае дальнейшее решение задачи происходит по одной и той же схеме. Исходя из этого, при программной реализации задачи для поиска начального решения был выбран метод «северо-западного» угла. Даже если при этом потребуется большее количество итераций для поиска оптимального решения, более выгодно использовать этот метод, так как в этом случае возрастает точность решения, при этом структура программы будет заметно проще.

Так как не известно: оптимален ли полученный опорный план или нет, то стоит провести оценки базисных и небазисных переменных. Для этого воспользуемся методом потенциалов.

В этом методе строке i и столбцу j ставятся в соответствие числа Ui и Vj. Для каждой базисной переменной Хij текущего решения потенциалы Ui иVj должны удовлетворять условию:

Ui + Vj. =Сij .

Если условия не выполняются то, для включения в базис выбирается небазисная переменная, имеющая самое большое положительное значение. Для нахождения выводимой переменной строится замкнутый цикл. Цикл начинается и заканчивается выбранной небазисной переменной. Он состоит из последовательности вертикальных и горизонтальных отрезков, концами которых должны быть небазисные переменные. Построение данного цикла необходимо для того, чтобы после ввода новой переменной сбалансировать значения базисных переменных.

Не существенно, в каком направлении происходит обход цикла. Для каждого базисного переменного и соответствующей небазисной переменной можно построить только один цикл. После построения цикла вводимой небазисной переменной ставится в соответствие знака «+», далее базисным переменным, находящимся в узлах цикла ставятся поочередно знаки «» и «+». Выводимой переменной считается базисная переменная, имеющая минимальное значение на местах со знаком «». Далее к базисным переменным, находящимся на местах со знаком «+» прибавляется это значение, из переменных со знаком «» – вычитается. Вводимой переменной присваивается найденное минимальное значение. После снова производятся оценки базисных и небазисных переменных и устанавливается, выполнены ли условия оптимальности.

19. 
    Основы теории игр. Предмет и задачи теории игр.
    

В процессе целенаправленной человеческой деятельности возникают ситуации, в которых интересы отдельных лиц (групп, сторон) либо прямо противоположны (антагонистичны), либо, не будучи непримиримыми, все же не совпадают. Такие ситуации называются конфликтными. Эффективность решений, принимаемых в ходе конфликта каждой из сторон, зависит от действий другой стороны. При этом ни одна из сторон не может полностью контролировать положение, т. к. и той и другой стороне решения приходится принимать в условиях неопределенности.

Теория игр – это математическая теория конфликтных ситуаций, разрабатывающая рекомендации по наиболее рациональному образу (стратегии) действий каждого из участников в ходе конфликтной ситуации (игры), т. е. таких действий, которые обеспечивали бы ему наилучший результат. Становление и систематическое изучение теории игр и ее приложений в экономике начинается с выходом в 1944 г. монографии Дж. фон Неймана и О. Моргенштерна «Теория игр и экономическое поведение».

20. 
    Основные понятия теории игр.
    

Игровую схему можно придать многим ситуациям в экономике. Здесь выигрышем могут быть эффективность использования ресурсов, производственных фондов, величина прибыли, себестоимость и т. д.

Игра – это совокупность правил, определяющих возможные действия (чистые стратегии) участников игры (игроков).

Суть игры в том, что каждый из участников принимает такие решения в развивающейся конфликтной ситуации, которые, как он полагает, обеспечивают ему наилучший результат (исход) игры. Игра – это упрощенная математическая модель конфликтной ситуации.

Стратегия – это совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры. Оптимальной стратегией называется стратегия, которая обеспечивает игроку наилучший исход игры при предположении, что противник использует наилучшую для себя стратегию.

Исход (плата) игры – это значение некоторой функции, которая называется функцией выигрыша (платежной функцией). Далее будем рассматривать только такие игры, в которых выигрыш выражается количественно: стоимостью, баллами и т. д. Величина выигрыша зависит от стратегии, применяемой игроками. Игроки – это участники игры с различными группами интересов. Партией называют каждый вариант реализации игры. В партии игроки совершают конкретные ходы.

Ход – это выбор и реализация игроком одного из допустимых вариантов поведения. Ходы бывают:

1) личные, когда игрок выбирает и реализует ту или иную свою конкретную чистую стратегию. Например, в шахматах каждый ход является личным;

2) случайные, когда выбор чистой стратегии производится с использованием какого-либо механизма случайного выбора (например, с применением таблицы случайных чисел).

21. 
    Матричные игры с нулевой суммой.
    

Матричная игра m× n (с нулевой суммой) – это антагонистическая игра, в которой первый игрок А использует возможные стратегии A₁, A₂, …, A_m, а его противник (оппонент) B – стратегии B₁, B₂, …, B_n. Если игрок A применит стратегию Ai, а оппонент – стратегию Bj, то плата a_ij игры будет выигрышем игрока А (проигрышем противника В) для a_ij > 0. Таким образом, игра с нулевой суммой полностью описывается так называемой платежной матрицей игры (табл. ).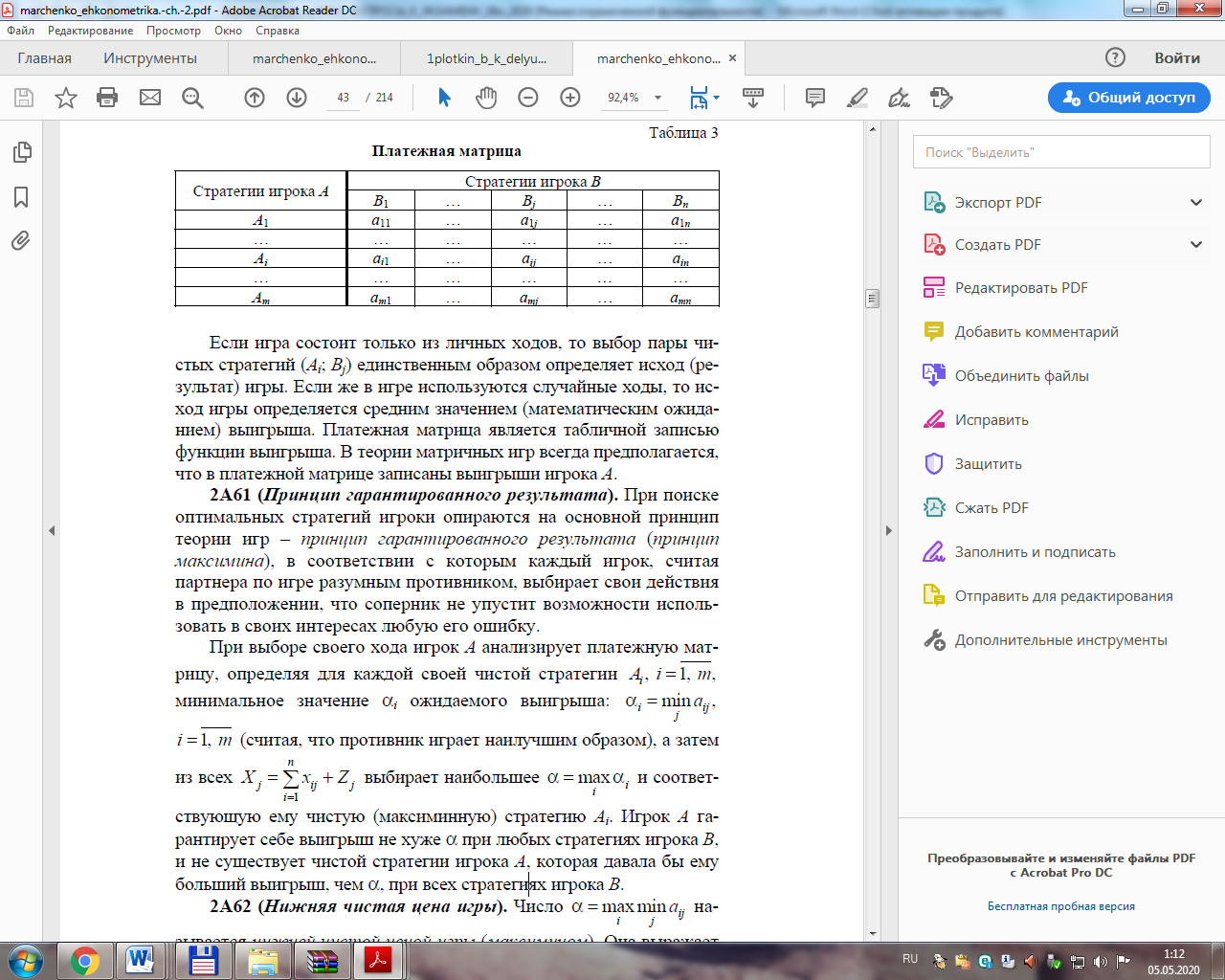


Если игра состоит только из личных ходов, то выбор пары чистых стратегий (Ai; Bj) единственным образом определяет исход (результат) игры. Если же в игре используются случайные ходы, то исход игры определяется средним значением (математическим ожиданием) выигрыша. Платежная матрица является табличной записью функции выигрыша. В теории матричных игр всегда предполагается, что в платежной матрице записаны выигрыши игрока А.

При поиске оптимальных стратегий игроки опираются на основной принцип теории игр – принцип гарантированного результата (принцип максимина), в соответствии с которым каждый игрок, считая партнера по игре разумным противником, выбирает свои действия

в предположении, что соперник не упустит возможности использовать в своих интересах любую его ошибку.

При выборе своего хода игрок А анализирует платежную матрицу, определяя для каждой своей чистой стратегии A_i , i =1, m, минимальное значение α_i ожидаемого выигрыша:
(считая, что противник играет наилучшим образом), а затем из всех
и соответствующую ему чистую (максиминную) стратегию Аi. Игрок А гарантирует себе выигрыш не хуже α при любых стратегиях игрока В, и не существует чистой стратегии игрока А, которая давала бы ему больший выигрыш, чем α, при всех стратегиях игрока В.

Число называется нижней чистой ценой игры (максимином). Она выражает выигрыш игрока А при использовании максиминной стратегии независимо от действий игрока В.

Число β, определяемое по формуле



называется верхней чистой ценой игры (минимаксом). Она показывает, какой максимальный проигрыш (гарантированный результат) может быть у игрока В при подходящем выборе им своей чистой стратегии (независимо от действий игрока А). Соответствующая стратегия игрока В называется минимаксной.

22. 
    Многокритериальная оптимизация.
    

23. 
    Метод экспертных оценок.
    

Метод экспертных оценок основан на построении единого показателя эффективности посредством суммирования произведения имеющихся показателей на соответствующие весовые коэффициенты (коэффициенты важности показателей).

Одним из распространенных методов определения степени относительной важности является назначение коэффициентов веса, которые, как правило, на ходят с помощью методов экспертных оценок. Назначение коэффициентов веса с помощью экспертизы представляет собой обычное обсуждение, стой разницей, что свое мнение эксперты выражают не словами, а цифрами. Методы экспертных оценок широко распространены в спорте. Нет основания считать неприемлемым коллективное мнение специалистов при принятии оптимальных решений. Существует множество методов определения экспертных оценок.

Один из них – метод непосредственного назначения коэффициентов веса. Согласно этого метода каждый i-й эксперт для каждого k-го параметра должен назначать коэффициент α_ik таким образом, чтобы сумма коэффициентов веса, назначенных одним экспертом для различных параметров, равнялась единице: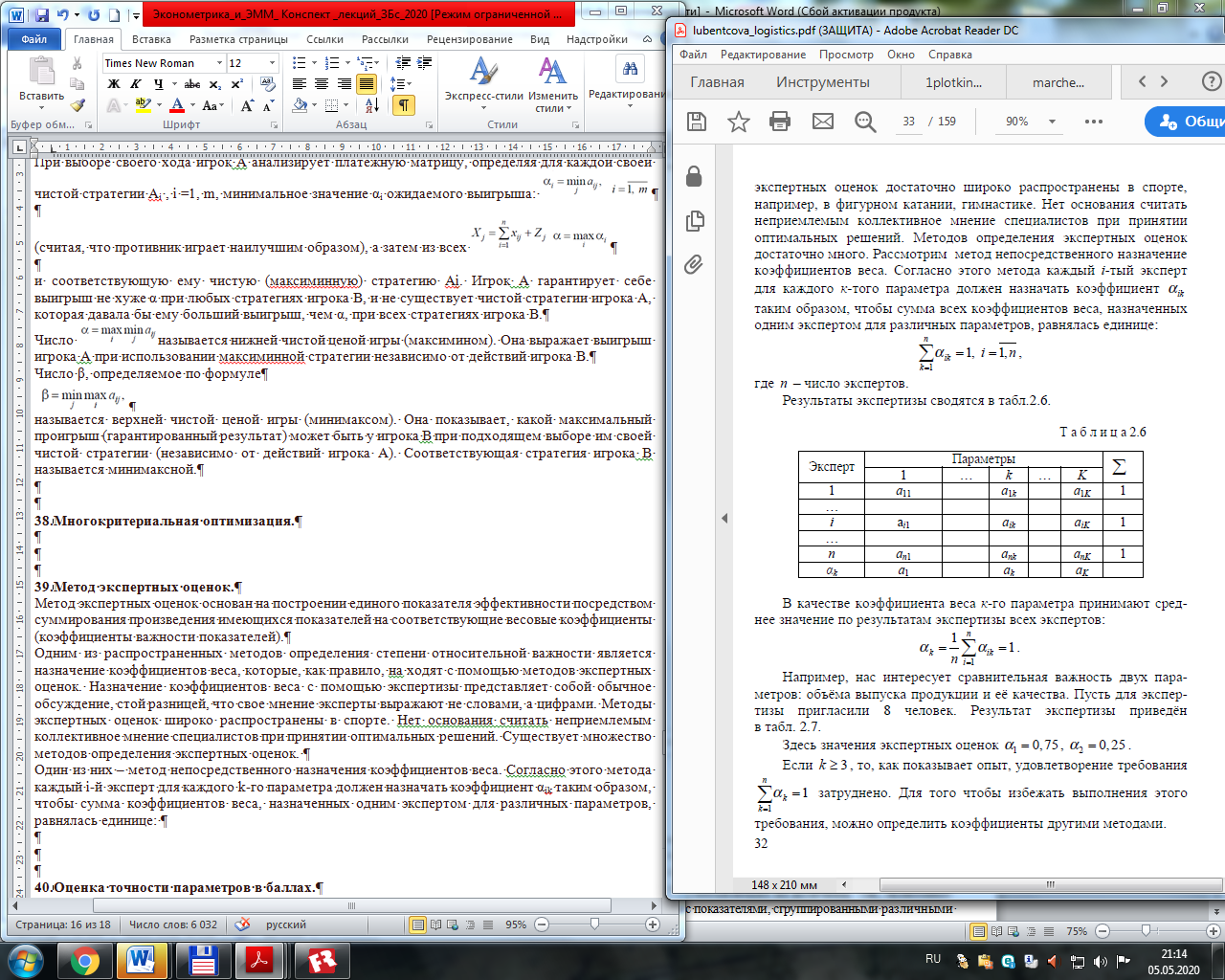



где n – число экспертов.

Результаты экспертизы сводятся в таблицу


В качестве коэффициента веса k-го параметра принимают среднее значение по результатам экспертизы всех экспертов:

24. 
    Оценка точности параметров в баллах.
    

В этом случает каждый i-й эксперт назначает каждому k-му параметру оценку по десятибалльной системе. Наиболее важный параметр оценивают более высоким баллом, при этом различным параметрам может быть назначен одинаковый балл. В результате экспертизы заполняется таблица.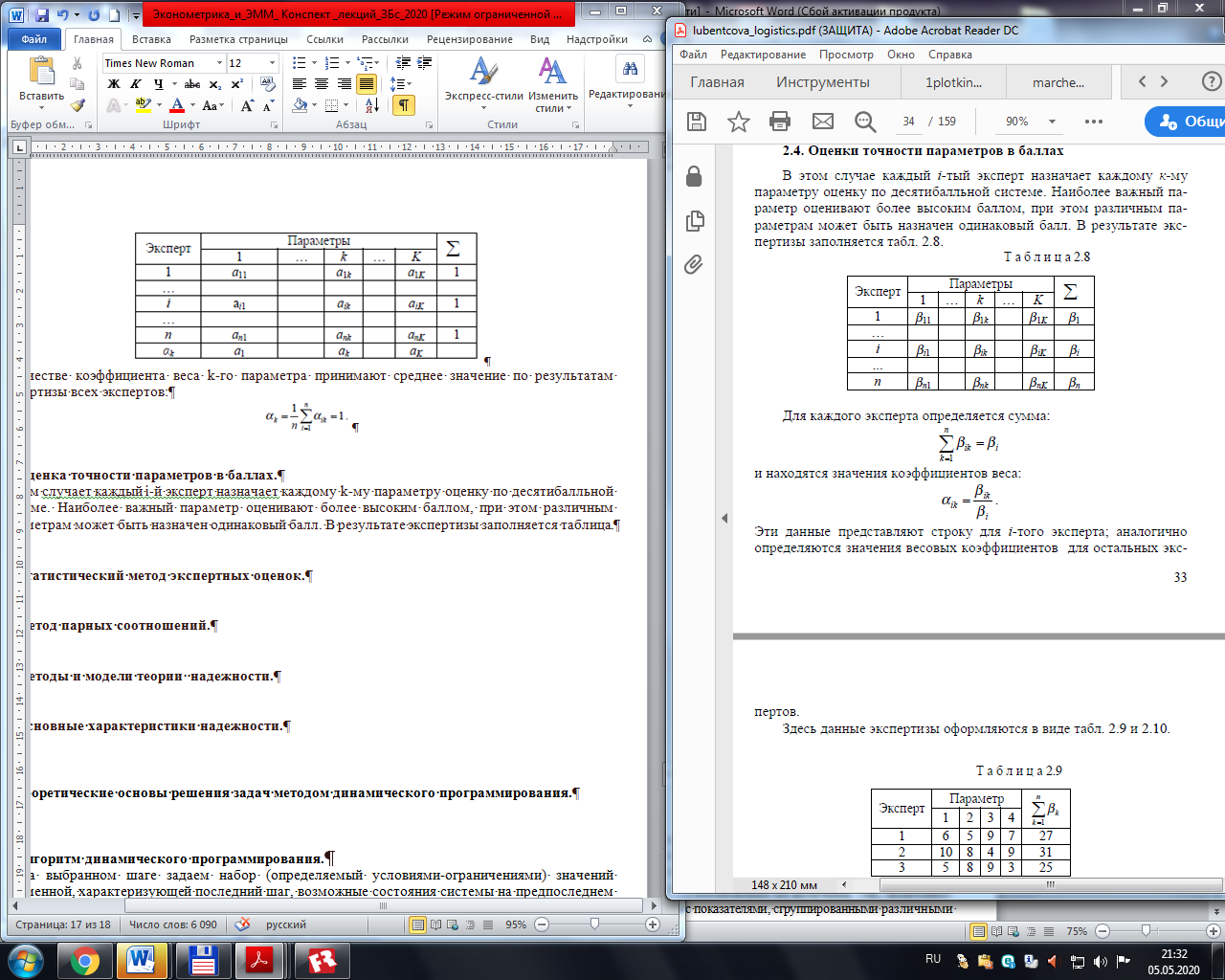



Для каждого эксперта определяется сумма:


и находятся значения коэффициентов веса:


Эти данные представляют строку для i-го эксперта; аналогично определяются значения весовых коэффициентов для остальных экспертов.

25. 
    Статистический метод экспертных оценок.
    

В результате опроса экспертов принимают среднее значение экспертных оценок. Такой подход не учитывает разброса оценок, даваемых каждым экспертом в отдельности, а разброс является показателем того, что либо вопрос поставлен недостаточно однозначно, либо признаком некомпетентности экспертов, либо следствием и того и другого. Вместе с тем, неучет разброса экспертных оценок может привести к неправильным выводам.

Для исключения этого недостатка необходимо исходить из того, что оценка, данная отдельным экспертом, представляет собой реализацию случайной величины и поэтому обработка результатов экспертизы должна производиться по правилам действий со случайными величинами. Проведение экспертизы рассматривается на примере определения коэффициентов веса α_i параметров х_i. Определение экспертных оценок ведется следующим образом:

1. 
   каждый эксперт должен независимо от других выразить количественно важность параметров х₁, х₂, … х_k , придав коэффициентам веса α₁, α₂, … α_k соответствующие значения таким образом, чтобы
   
2. 
   приведенные результаты эксперимента свести в таблицу,
   
3. 
   по результатам произведенной экспертизы для каждого коэффициента веса найти оценку математического ожидания, затем определить отклонение в оценке каждого эксперта от оценки математического ожидания и составить новую таблицу.
   
4. 
   обсудить результаты проведенной экспертизы, предоставить слово для обоснования своей оценки в первую очередь там экспертам, у которых отклонения наибольшие, с помощью вопросов и общей дискуссии добиться устранения возможного недопонимания того, что имеется в виду под оцениваемыми факторами
   
5. 
   провести повторную экспертизу, результаты которой свести в таблицу экспертных оценок, затем по данным таблицы определяются оценки математического ожидания и оценки дисперсий, которые сводятся в новую таблицу.
   
6. 
   при обработке окончательных результатов экспертизы для характеристики степени согласия мнения исследователей о ранжировке коэффициентов веса вычисляют коэффициент конкордации.
   

26. 
    Алгоритм динамического программирования.
    

1. На выбранном шаге задаем набор (определяемый условиями-ограничениями) значений переменной, характеризующей последний шаг, возможные состояния системы на предпоследнем шаге. Для каждого возможного состояния и каждого значения выбранной переменной вычисляем значения целевой функции. Из них для каждого исхода предпоследнего шага выбираем оптимальные значения целевой функции и соответствующие им значения рассматриваемой переменной. Для каждого исхода предпоследнего шага запоминаем оптимальное значение переменной (или несколько значений, если таких значений больше одного) и соответствующее значение целевой функции. Получаем и фиксируем соответствующую таблицу.

2. Переходим к оптимизации на этапе, предшествующем предыдущему (движение "вспять"), отыскивая оптимальное значение новой переменной при фиксированных найденных ранее оптимальных значениях следующих переменных. Оптимальное значение целевой функции на последующих шагах (при оптимальных значениях последующих переменных) считываем из предыдущей таблицы. Если новая переменная характеризует первый шаг, то переходим к п.З. В противном случае повторяем п.2 для следующей переменной.

З. При данном в задаче исходном условии для каждого возможного значения первой переменной вычисляем значение целевой функции. Выбираем оптимальное значение целевой функции, соответствующее оптимальному(ым) значению(иям) первой переменной.

4. При известном оптимальном значении первой переменной определяем исходные данные для следующего (второго) шага и по последней таблице - оптимальное(ые) значение(ия) следующей (второй) переменной.

5. Если следующая переменная не характеризует последний шаг, то переходим к п.4. Иначе переходим к п.6.

6.Формируем (выписываем) оптимальное решение.