Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика

• Название: Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
• Анкор: Лекции по МОР.docx
• Дата: 02.05.2017
• Размер: 1.02 Mb.
• Имя файла: Лекции по МОР.docx
• Тип: Конспект лекций; #6625
• страница: 2 из 16

1.2. Математическая формализация

Для исследования характеристик процесса функционирования любой системы математическими методами, включая и компьютерное моделирование, должна быть проведена формализация этого процесса, то есть построена математическая модель. Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее устанавливать ее свойства, характеризующие, в конечном счете, свойства моделируемого объекта.

Вид математической модели зависит от природы реального объекта, задач исследования, требуемой достоверности и точности решения этих задач, наконец, от вкуса и квалификации исследователя.

Модель – это условный образ исследуемого объекта, который приближенно воссоздает этот объект с помощь некоторого языка. В экономико-математических моделях таким объектом является экономический процесс (например, планирование производства, использование мощностей и др.), а языком – математические методы.

Экономико-математическая модель – это математическое описание исследуемого экономического процесса или объекта.

Примерами экономико-математических моделей являются модели потребительского выбора, модели фирмы, модели экономического роста, модели равновесия на товарных, факторных и финансовых рынках и другие. При построении моделей экономисты выявляют существенные факторы, которые определяют исследуемое явление, и отбрасывают детали, несущественные для решения поставленной проблемы. Формализация основных особенностей функционирования экономических объектов позволяет оценить возможные последствия воздействия на них и использовать такие оценки в управлении.

Применение математического моделирования при принятии решений предполагает последовательное осуществление трех этапов исследования.

Первый – от исходной практической проблемы до теоретической чисто математической задачи.

Второй – математическое изучение и решение этой задачи.

Третий – переход от математических выводов обратно к практической проблеме.

В области моделирования задач принятия решений, как и в иных областях применения математики, выделяют четверку проблем: задача – модель – метод – условия применимости.

Задача, как правило, порождена потребностями той или иной прикладной области. При этом происходит одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей у маркетологов возникает вопрос: различаются ли мнения двух групп потребителей?

При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин. Вопрос маркетологов в рамках этой модели переформулируется в вопрос о проверке той или иной статистической гипотезы однородности, например, о проверке равенства математических ожиданий или о совпадении функций распределения двух совокупностей.

Задача может возникнуть при обобщении потребностей ряда прикладных областей. Необходимости проверки упомянутой гипотезы однородности возникает и в медицине при сравнении двух групп пациентов, в технике при сопоставлении результатов обработки деталей двумя способами и в других областях. Следовательно, одна и та же математическая модель может применяться для решения разных по прикладной сущности задач.

Другими словами, следует различать математическую структуру модели и ее экономическое содержание. Рассмотрим два простых примера².

Пример 1. Пусть требуется определить, какую сумму следует положить в банк при заданной ставке процента (20 % годовых), чтобы через год получить 12000долл.?

Введем формальные обозначения для величин рассматриваемой задачи:

М₀ – начальная сумма денег;

М₁ – конечная сумма денег;

r – ставка процента.

Запишем соотношение между ними (математическую модель):

М₁= М₀ (1+r/100).

Найдем требуемую величину из решения основного уравнения модели: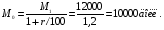



Пример 2. Пусть требуется определить, каков был объем выпуска продукции предприятия, если в результате технического перевооружения средняя производительность труда увеличилась на 20 %, и предприятие стало выпускать 12000 единиц продукции.

Введем формальные обозначения для величин рассматриваемой задачи:

Q₀– начальный выпуск;

Q₁ – конечный выпуск;

r– процент прироста производительности.

Запишем соотношение между ними (математическую модель):

Q₁= Q₀ (1+r/100).

Найдем требуемую величину из решения основного уравнения модели: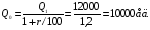



Сравнивая полученные модели и результаты, можно заметить, что математическая форма модели имеет вид:

Х₁= Х₀ (1+r/100),

который является одинаковым для обоих примеров, как и числовые значения входящих в нее величин и результатов. Однако экономическая ситуация, описываемая моделью и экономическое содержание модели и результатов расчета совершенно различны. Таким образом, одни и те же математические модели и методы могут быть использованы для решения совершенно разных экономических задач.

Метод, используемый в рамках определенной математической модели – это дело математиков. Для решения задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов. Например, центральная предельная теорема теории вероятностей была получена такими разными методами, как: теорема Муавра – Лапласа, метод моментов Чебышева, метод характеристических функций Ляпунова, метод Линдеберга и метод Феллера. Для проверки гипотезы однородности могут использоваться методы Смирнова, Лемана – Розенблата, Вилкоксона и др.

Условия применимости – полностью математический элемент четверки. С точки зрения математика замена условия дифференцируемости некоторой функции на условие ее непрерывности представляет существенное научное достижение, в то время как для прикладного исследователя, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от дифференцируемых. Точнее, они одинаково могут быть использованы для описания реальной действительности.

Экономические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее поведение объекта при изменении каких-либо параметров. Предсказания будущих изменений, например, повышение обменного курса, ухудшения экономической конъюнктуры, падение прибыли может опираться только на интуицию. Но при этом могут быть упущены, неправильно определены или неверно оценены важные взаимосвязи экономических показателей, влияющих на рассматриваемую ситуацию. В модели все взаимосвязи переменных могут быть оценены количественно, что позволяет получить более качественный и надежный прогноз.

По своему определению любая экономическая модель абстрактна и, следовательно, неполна, поскольку она включает наиболее существенные факторы, определяющие закономерности функционирования рассматриваемого экономического объекта, она абстрагируется от других факторов, которые, несмотря на свою относительную малость, все же в совокупности могут определять не только отклонения в поведении объекта, но и само его поведение. Так, в простейшей модели спроса считается, что величина спроса на товар определяется его ценой и доходом потребителя. На самом же деле на величину спроса оказывает также влияние ряд других факторов: вкусы и ожидания потребителей, цены на другие товары, воздействие рекламы, моды и т.п. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказывают на объект относительно малое результирующее воздействие в интересующем исследователя аспекте. Состав учтенных в модели факторов и ее структура могут быть уточнены в ходе совершенствования модели.