Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика

• Название: Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
• Анкор: Лекции по МОР.docx
• Дата: 02.05.2017
• Размер: 1.02 Mb.
• Имя файла: Лекции по МОР.docx
• Тип: Конспект лекций; #6625
• страница: 7 из 16

Лекция 3. Линейное программирование

План.

3.1.Линейное программирование как инструмент математического моделирования экономики.

3.2. Примеры моделей линейного программирования.

3.1. Линейное программирование как инструмент математического моделирования экономики

Линейное программирование сформировалось как отдельный раздел прикладной математики в 40 – 50-х гг. ХХ в. благодаря работам советского ученого, лауреата Нобелевской премии Л.В. Канторовича. В 1939 году им была опубликована работа «Математические методы организации и планирования производства», в которой он с использованием математики решил экономические задачи о наилучшей загрузке машин, раскрое материалов с наименьшими расходами, распределении грузов по нескольким видам транспорта и другие, предложив метод разрешающих множителей⁸.

Л.В. Канторович впервые сформулировал такие широко используемые экономико-математические понятия, как оптимальный план, оптимальное распределение ресурсов, объективно обусловленные оценки, указав многочисленные области экономики, где они могут быть применены.

Понятие линейного программирования было введено американским математиком Д. Данцигом, который в 1949 г. предложил алгоритм решения задачи линейного программирования, получивший название «симплексный метод».

Математическое программирование, в которое входит линейное программирование, в настоящее время является одним из направлений исследования операций. В зависимости от вида решаемых задач в нем выделяют такие области, как линейное, нелинейное, дискретное, динамическое программирование и др. Термин «программирование» введен в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу или план работы некоторого экономического объекта.

В классическом математическом анализе исследуются общая постановка задачи определения условного экстремума. Однако в связи с развитием промышленного производства, транспорта, агропромышленного комплекса, банковского сектора традиционных результатов математического анализа оказалось недостаточно. Потребности практики и развитие вычислительной техники привели к необходимости определения оптимальных решений при анализе сложных экономических систем.

Главным инструментом для решения таких задач является математическое моделирование. При этом сначала строится простая модель, затем проводится ее исследование, позволяющее понять, какие из интегрирующих свойств объекта не улавливаются формальной схемой, после чего за счет усложнения модели обеспечивается большая ее адекватность реальности. Во многих случаях первым приближением к действительности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, являются линейными. Практика показывает, что достаточное количество экономических процессов достаточно полно описывается линейными моделями. Следовательно, линейное программирование как аппарат, позволяющий отыскивать условный экстремум на множестве, заданном линейными уравнениями и неравенствами, играет важную роль при анализе этих процессов.

Линейное программирование получило широкое развитие в связи с тем, что было установлено: ряд задач сферы планирования и управления может быть сформулирован в виде задач линейного программирования, для решения которых имеются эффективные методы. По оценкам специалистов примерно 80–85 % всех решаемых на практике задач оптимизации относится к задачам линейного программирования.

Созданный математический аппарат в сочетании с компьютерными программами, производящими трудоемкие расчеты, позволяет широко использовать модели линейного программирования в экономической науке и практике.

Определение 1⁹. Линейное программирование (ЛП) – это область математического программирования, являющегося разделом математики и изучающего методы поиска экстремальных (наибольших и наименьших) значений линейной функции конечного числа переменных, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые представляют количественные соотношения между переменными, выражающие условия и требования экономической задачи и математически записываются в виде уравнений или неравенств, называются системой ограничений.

К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения.

Общая задача линейного программирования (ЗЛП) состоит в нахождении экстремального значения (максимума или минимума) линейной функции, называемой целевой¹⁰: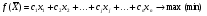

(3.1)

от nпеременных x₁, x₂, …, х_n при наложенных функциональных ограничениях:

(3.2)

и прямых ограничениях (требовании неотрицательности переменных)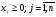

, (3.3)

где a_ij, b_i, c_j – заданные постоянные величины.

В системе ограничений (3.2) знаки «меньше или равно», «равно», «больше или равно» могут встречаться одновременно.

ЗЛП в более краткой записи имеет вид: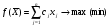

,

при ограничениях: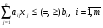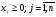

;

.

Вектор Х = (x₁, x₂, …, х_n) компоненты которого удовлетворяют функциональным и прямым ограничениям задачи называют планом (или допустимым решением) ЗЛП.

Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений (ОДР). Допустимое решение, которое доставляет максимум или минимум целевой функции f(X), называется оптимальным планом задачи и обозначается f(X^*), где Х^*=(x₁^*,  x₂^*, …, х_n^*).

Еще одна форма записи ЗЛП: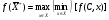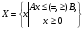



,

где f(X^*) есть максимальное (минимальное) значение f(С, х), взятое по всем решениям, входящим в множество возможных решений Х.

Определение 2¹¹. Математическое выражение целевой функции и ее ограничений называются математической моделью экономической задачи.

Для составления математической модели необходимо:

1) обозначить переменные;

2) составить целевую функцию исходя из цели задачи;

3) записать систему ограничений, учитывая имеющие в условии задачи показатели и их количественные закономерности.