Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
4.2. Геометрическая интерпретация задачи линейного программированияРассмотрим следующую задачу линейного программирования16: 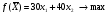 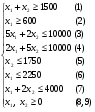 На рис. 4.1 представлено множество допустимых точек, удовлетворяющих всем ограничениям задачи и представляющее собой пересечение полуплоскостей, отражающих ограничения задачи линейного программирования. 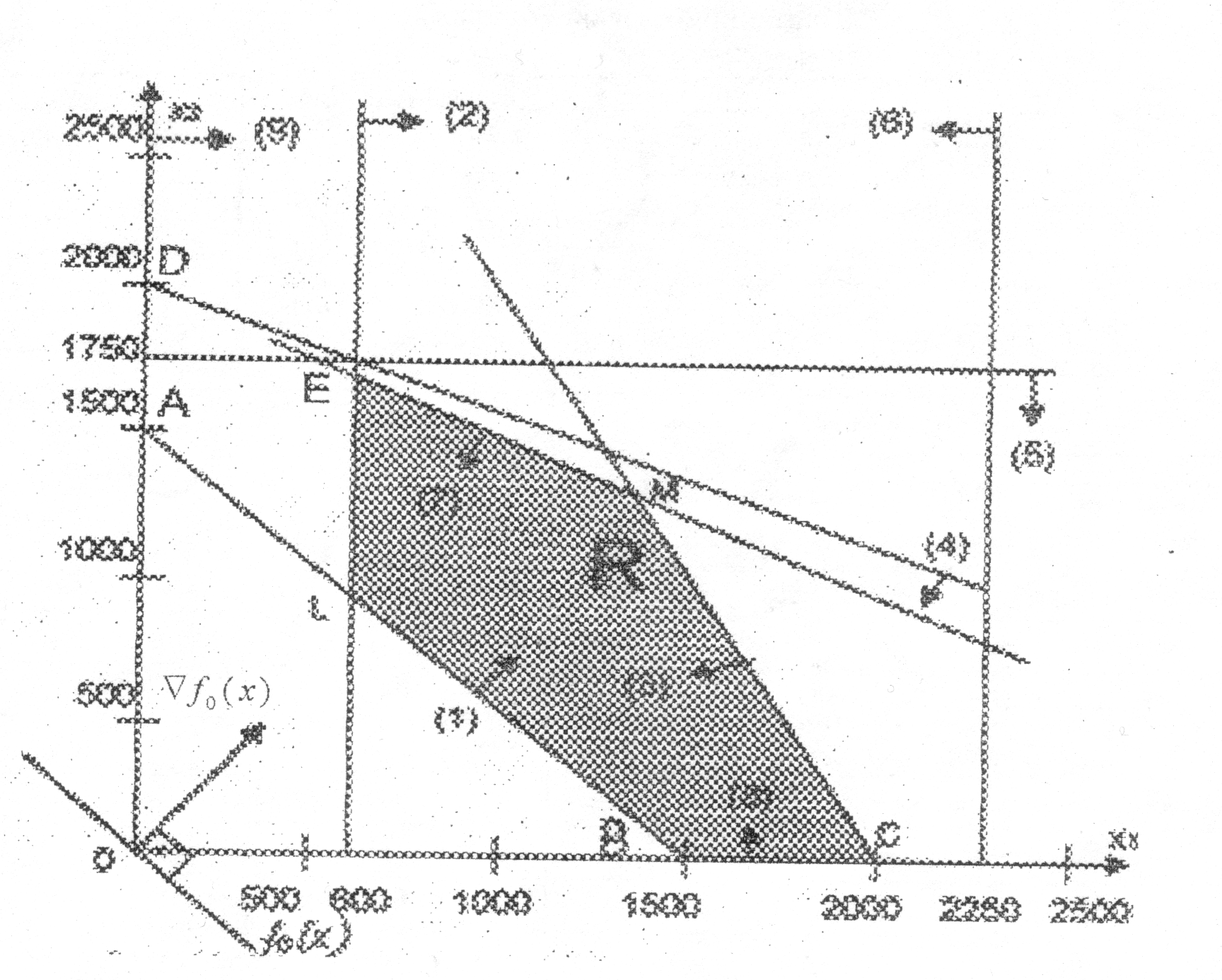 Рис. 4.1. Геометрическая интерпретация решения задачи Геометрическую интерпретацию имеют ЗЛП с двумя переменными. Исследуем целевую функцию 30х1 + 40х2. Данной целевой функции соответствует семейство прямых 30х1 + 40х2 = L, представляющих собой множество параллельных прямых, каждая из которых соответствует определенному значению параметра L. Тогда задачу линейного программирования можно сформулировать следующим образом. Найти такое максимальное значение L, при котором прямая 30х1 + 40х2 = L пересекает допустимое множество. В общем случае с геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на которой достигается самая верхняя (нижняя) линия уровня (прямая, отражающая целевую функцию), расположенная дальше (ближе) остальных в направлении наискорейшего роста. Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент целевой функции f(X) на плоскости Х1ОХ2. Этот вектор показывает направление наискорейшего изменения целевой функции, он равен 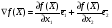 , ,где 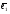 и и 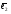 единичные векторы по осям ОХ1 и ОХ2 соответственно. Таким образом, f(X) = (f/x1, (f/x2). Координатами вектора-градиента целевой функции f(X) являются коэффициенты целевой функции f(X). единичные векторы по осям ОХ1 и ОХ2 соответственно. Таким образом, f(X) = (f/x1, (f/x2). Координатами вектора-градиента целевой функции f(X) являются коэффициенты целевой функции f(X).В рассматриваемом примере, если двигать прямую 30х1 + 40х2 = L из начала координат по направлению вектора-градиента целевой функции, то точкой, в которой достигается самая верхняя линия уровня является точка М пересечения прямых 5x1 + 2x2 = 10000 и x1 + 2x2 = 4000 с координатами x1 = 1500 и x2 = 1250. Таким образом, оптимальное решение достигается в точке М (1500; 1250). При этом значение целевой функции составит f(X*) =30 * 1500 + 40 * 1250 = 95000. На этом примере можно увидеть основные свойства задач линейного программирования: допустимое множество точек представляет собой выпуклый многоугольник, получившийся в результате пересечения полуплоскостей и наибольшее значение целевой функции достигается в его вершине – крайней точке. Решение задачи линейного программирования может быть не единственным, а состоять из бесконечного числа точек. Таким образом, решение задачи линейного программирования состоит в следующем: необходимо построить многоугольник допустимых точек, найти его вершины и выбрать из них те, координаты которых придают максимальное значение целевой функции. Лекция 5. Симплексный метод решения задачи линейного программированияПлан. 5.1. Симплекс-метод. 5.2.Симплексные таблицы и алгоритм решения задач. 5.3. Применение симплексного метода в экономических задачах. 5.1. Симплекс-методСимплексный метод является универсальным, так как позволяет решать практически любую задачу линейного программирования, заданную в каноническом виде. Идея симплекс метода была разработана русским ученым Л.В. Канторовичем в 1939 г. На основе этой идеи американский ученый Д. Данцинг в 1949 г. разработал симплекс-метод, позволяющий решать любую задачу линейного программирования. В настоящее время на основе этого метода разработан пакет программ для решения задач линейного программирования. Идея симплексного метода (метода последовательного улучшения плана) заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по опорным решениям задачи к оптимальному. При этом перемещении значение целевой функции для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оптимальное опорное решение. Симплексный метод состоит из трех основных элементов: 1) определения какого-либо первоначального допустимого базисного решения задачи; 2) правила перехода к лучшему решению; 3) проверки оптимальности допустимого решения. Симплекс-метод состоит из двух вычислительных процедур: - симплекс-метод с естественным базисом; - симплекс-метод с искусственным базисом. Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи линейного программирования к каноническому виду. Для применения симплекс-метода с естественным базисом ЗЛП в каноническом виде должна содержать единичную подматрицу порядка m, в этом случае очевиден первоначальный опорный план (неотрицательное базисное решение системы ограничений). Симплексный метод с искусственным базисом применяется при отсутствии первоначального опорного плана исходной ЗЛП в каноническом виде. Такая ситуация возникает при наличии в исходном ограничении знаков «равно» либо «больше или равно». |
