Лекции по МОР. Конспект лекций по дисциплине методы оптимальных решений Направление подготовки 080100 Экономика
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
Лекция 6. Метод искусственного базиса решения задачи линейного программированияПлан. 6.1. Метод искусственного базиса. 6.2. Применение метода искусственного базиса. 6.1. Метод искусственного базисаПри решении задач симплексным методом необходимо, чтобы модель задачи была канонической и система ограничений была приведена к единичному неотрицательному базису. Встречаются случаи, когда эти преобразования оказываются громоздкими19. Метод искусственного базиса дает возможность решать задачи, приведенные к каноническому виду, без предварительного нахождения опорного решения. Дана задача линейного программирования: 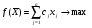 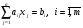 , ,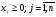 . .Из этой задачи составим вспомогательную задачу следующим образом: 1) систему ограничений вспомогательной задачи получаем из системы ограничений исходной, добавляя в каждое ограничение, не содержащее базисную переменную, искусственную базисную переменную; 2) целевая функция равна алгебраической сумме искусственных переменных, взятых с коэффициентом (-1); 3) условие неотрицательности распространяется на все переменные, в том числе и искусственные. Математическая модель вспомогательной задачи: 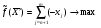 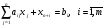 , ,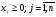 . .Система ограничений вспомогательной задачи приведена к единичному базису, поэтому она имеет решение: 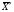 = (0, 0, , 0, b1, b2, , bn), = (0, 0, , 0, b1, b2, , bn),при этом 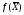 0. 0.Между оптимальным решением вспомогательной задачи и опорным решением исходной задачи существует зависимость: 1) если 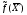 = 0 достигается при = 0 достигается при 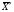 = (l1, l2, , ln, 0, 0, , 0), то = (l1, l2, , ln, 0, 0, , 0), то 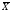 = (l1, l2, , ln) является исходным опорным решением; = (l1, l2, , ln) является исходным опорным решением;2) если max 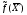 0, то ограничения исходной задачи несовместны. 0, то ограничения исходной задачи несовместны.6.2. Применение метода искусственного базисаПрименение метода искусственного базиса рассмотрим на следующем примере20: 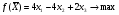 при ограничениях: 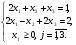 Решение. Составим вспомогательную задачу: 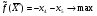 при ограничениях: 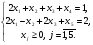 Решим вспомогательную задачу симплексным методом:
Решение вспомогательной задачи: 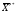 = (0, 0, 1, 0, 0), = (0, 0, 1, 0, 0), 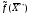 = 0, = 0,Исходное опорное решение данной задачи: 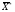 = (0, 0, 1). = (0, 0, 1).Проверим это решение на оптимальность:
Ответ: 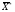 = (0, 0, 1), = (0, 0, 1), 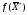 = 2. = 2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
