Инфор.технологии - Решение задач оптимизации. Федеральное агенство по образованию
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Тверской государственный технический университет Линейное программирование. Примеры решения задач в Excel. Тверь 2008 Методическое пособие предназначено для студентов специальности «Экономика и управление на предприятии (машиностроение)», изучающих курсы «Экономико-математические методы в управлении» и «Экономико-математические модели объектов отрасли». Пособие можно также рекомендовать студентам экономических специальностей, изучающих экономико-математические методы и модели. Обсуждено и рекомендовано на заседании кафедры ИПМ (протокол № от марта 2008 г.) Составители: Е.Е. Фомина, И.Л. Кислова
СОДЕРЖАНИЕ Введение В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции). Оптимизационные модели отражают в математической форме смысл экономической задачи. Отличительной особенностью этих моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности. Общая задача оптимизации В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции f (x1, x 2, …. x n) при условиях gi (x1 , x2 ,…, x n ) ≤ bi ; ( i = 1,2, … m), где f и gi - заданные функции, а bi - некоторые действительные числа. Задачи математического программирования делятся на задачи линейного и нелинейного программирования. Если все функции f и gi - линейные, то соответствующая задачи является задачей линейного программирования (ЗЛП). Если хотя бы одна из указанные функций – нелинейная, то соответствующая задача является задачей нелинейного программирования. Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные. К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения. Cреди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения. Отдельными классами задач математического программирования являются задачи целочисленного, параметрического и дробно-линейного программирования. В общем виде задачи линейного программирования (ЗЛП) ставится следующим образом: Необходимо найти вектор и удовлетворяющий условиям где Линейная функция f(X) называется целевой функцией задачи. Условия (2) называются функциональными, а (3) – прямыми ограничениями задачи. Вектор X=(x1 , x2, … xn ), компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП. Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f (X ), называется оптимальным планом задачи. Будем считать, что ЗЛП записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательные. На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным: определения оптимальной производственной программы; оптимального смешивания компонентов; оптимального раскроя; оптимального размещения предприятий некоторой отрасли на определенной территории; формирования оптимального портфеля ценных бумаг; транспортной задачи. Для решения ЗЛП существует универсальный метод – метод последовательного улучшения плана, или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом (М-метод). Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду задачи линейного программирования (КЗЛП): В теории линейного программирования показано, что оптимальное решение ЗЛП связано с угловыми (крайними) точками многогранника решений, которым отвечают опорные планы (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А1,А2, …..Аn. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний Cm. Решение ЗЛП симплекс-методом «вручную» подробно рассмотрено в [1], [5] и др. ЗЛП широко применяются в экономике и управлении. На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным:
Менеджер, как лицо ответственное за принятие решений, должен уметь использовать известные модели и понимать как полученный результат использовать для принятия разумного решения. Огромный вклад в развитие и применение ЗЛП внес наш соотечественник Леонид Витальевич Канторович. За что в 1975 г. Был удостоен Нобелевской премии по экономике. 1 Методические указания по решению ЗЛП в среде Exсel 1.1 Максимизация прибыли предприятия Постановка задачи Для выпуска 4 - х видов продукции требуется сырье, рабочее время и оборудование. Для выпуска одной единицы продукции 1 - ого вида необходимо 3 ед. сырья, 22 ед. рабочего времени и 10 ед. оборудования. Для выпуска одной единицы продукции 2 - ого вида необходимо 5 ед. сырья, 14 ед. рабочего времени и 14 ед. оборудования. Для выпуска одной единицы продукции 3 - его вида необходимо 2 ед. сырья, 18 ед. рабочего времени и 8 ед. оборудования. Для выпуска одной единицы продукции 4 - ого вида необходимо 4 ед. сырья, 30 ед. рабочего времени и 16 ед. оборудования. Прибыль от продажи одной единицы продукции 1 - ого вида 30 руб., 2 - ого вида – 25 руб., 3 - его вида – 8 руб., 4 - ого вида – 16 руб. Ресурсы ограниченны: имеется 60 ед. сырья, 400 ед. рабочего времени и 120 ед. оборудования. А) Какое количество продукции каждого вида необходимо выпустить, чтобы максимизировать прибыль предприятия? Б) Все ли продукты вошли в оптимальный план или существуют убыточные? На сколько нужно увеличить прибыль от продажи одной единицы убыточной продукции, чтобы она вошла в оптимальный план? В) Каковы интервалы устойчивости для прибыли за одну единицу продукции каждого вида? Изменится ли оптимальное решение, если прибыли от продажи одной единицы продукции 4 – ого вида увеличить на 15 ед., 33 ед.? Уменьшить на 10 ед.? Г) Какие ресурсы являются дефицитными? Как изменится оптимальное решение, если ресурс оборудование увеличить на 1 ед., уменьшить на 100 ед., 50 ед.? Для удобства сведем данные задачи в следующую таблицу: Таблица 1
Решение I этап: Составление математической модели Элементы модели:
Так как в задаче требуется определить количество продукции каждого вида, то введем следующие переменные: x1 –количество единиц продукции 1 - ого вида, x2– количество единиц продукции 2 - ого вида, x3 –количество единиц продукции 3 - его вида, x4 –количество единиц продукции 4 - ого вида.
Т.к. цель задачи – максимизировать прибыль от продажи продукции (Р), то Р будет иметь вид: Р=30*x1+25*x2+8*x3+16* x4(руб.) (*)
Исходя из выражения для целевой функции, можно увидеть, что чем больше будут значенияx1, x2, x3 ,x4, тембольше будет прибыль Р. Однако беспредельно увеличивать выпуск продукции невозможно, т.к. ресурсы предприятия ограничены, что приводит к ограничениям на x1, x2, x3 ,x4. 3*x1+5*x2+2*x3+4*x4 22*x1+14*x2+18*x3+30*x4 10*x1+14*x2+8*x3+16*x4 xi Примечание:
Таблица 2
II этап: Решение задачи на ЭВМ в среде MS Excel
На начальном этапе присваиваем неизвестным произвольные значения, например, предполагаем, что выпуск каждой продукции составляет 1 единицу (см. рис. 1). 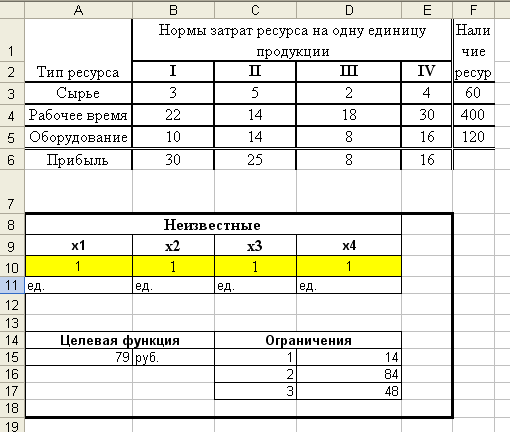 Рис.1 Оформление задачи в Excel
Для удобства ввода ЦФ и ограничений рекомендуется воспользоваться функцией СУММПРОИЗВ(). СУММПРОИЗВ() - перемножает соответствующие элементы заданных массивов и возвращает сумму произведений. Например, при вводе формулы для ЦФ аргументами функции СУММПРОИЗВ(A10:D10;B6:E6) будут диапазоны ячеек с неизвестными A10:D10 - (x1, x2, x3 ,x4) и прибылью за единицу продукции B6:E6 - (30,25,8,16). При вводе формул для целевой функции и ограничений необходимо делать ссылки на ячейки созначениями неизвестных A10:D10, а не на ячейки с именами неизвестных A9:D9. Ограничение (4) и знаки “ В ячейках D15:D17 занесены левые части ограничений, правые части ограничений содержаться в ячейках F3:F5.     левые части ограничений правые части ограничений Рис.2 Ввод целевой функции и ограничений
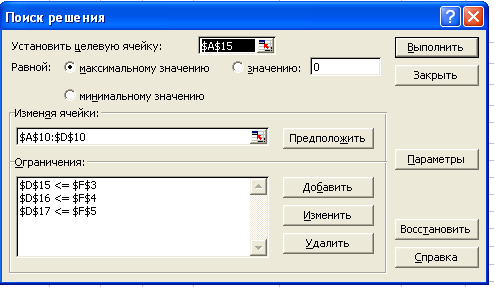 Рис.3 Поиск решения
В окне Установить целевую ячейку указываем адрес ячейки с целевой функцией А15. В разделе Равной указать Максимальном значению. Примечание: Для заполнения окна Установить целевую ячейку необходимо поставить курсор в это окно и на листе выделить ячейку, в которой содержится значение целевой функции.
В окно Изменяя ячейки вносим адреса ячеек с неизвестными задачи A10:D10. Примечание: Для заполнения окна Изменяя ячейки необходимо поставить курсор в это окно и на листе выделить ячейки, в которых содержатся значения переменных. Примечание: Для ввода неизвестных можно нажать кнопку Предположить.
Для ввода ограничений необходимо перейти в поле Ограничения и нажать кнопку Добавить. В появившемся диалоговом окне Добавление ограничения, последовательно, для каждого неравенства, в разделе Ссылка на ячейку указать адрес ячейки, соответствующей левой части ограничения, а в разделе Ограничения – адрес правой части ограничения. 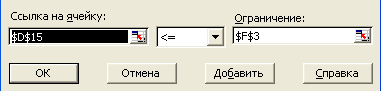 Рис. 4 Ввод ограничения 1  Рис. 5 Ввод ограничения 2 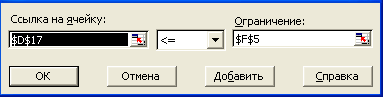 Рис. 6 Ввод ограничения 3
Для установки параметров модели необходимо нажать кнопку Параметры и в появившемся диалоговом окне Параметры поиска решения поставить галочки напротив переключателей Линейная модель и Неотрицательные значения (см. рис. 7).  Рис. 7 Параметры поиска решения Примечание: Полученная модель будет являться линейной, т.к. целевая функция и функциональные ограничения являются линейными.
После ввода всех данных необходимо нажать кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решения (см. рис. 8). Для отображения решения нужно выбрать переключатель Сохранить найденное решение и в окне Тип отчета выделить строку Устойчивость. Получение данных по устойчивости требуется для проведения анализа решения задачи и ответа на вопросы Б) – Д).  Рис. 8 Результат поиска решения Ответ В результате решения задачи был получен следующий ответ: необходимо выпускать 12 ед. продукции первого вида, продукцию второго, третьего и четвертого вида выпускать не нужно При этом максимальная прибыль составит 360 руб. 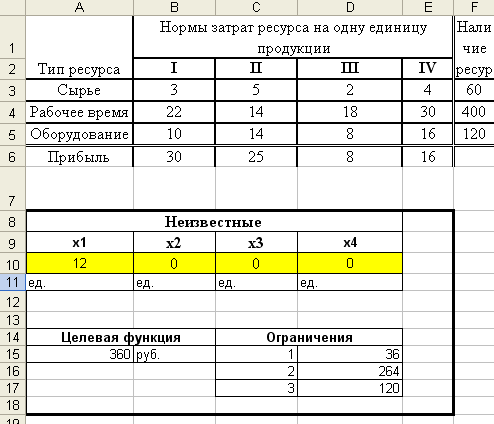 Рис. 9 результат решения задачи III этап: Анализ решения задачи В результате решения задачи в рабочей книги появится новый лист Отчет по устойчивости (только при выборе пункта Устойчивость в диалоговом окне Результат поиска решения), который необходим для проведении анализа полученного решения. Грамотно проанализировать решение задачи – одна из главных задач менеджера! Данные на листе организованны в виде двух таблиц: Изменяемые ячейки и Ограничения (см. рис. 10). 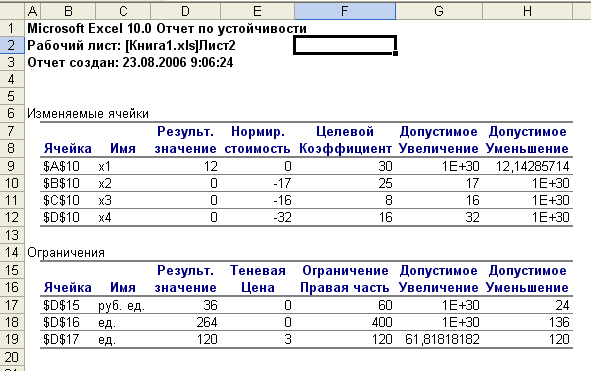 рис. 10 Отчет по устойчивости Таблица 3 | ||||||||||||||||||||||||||||||||||||||||||||
