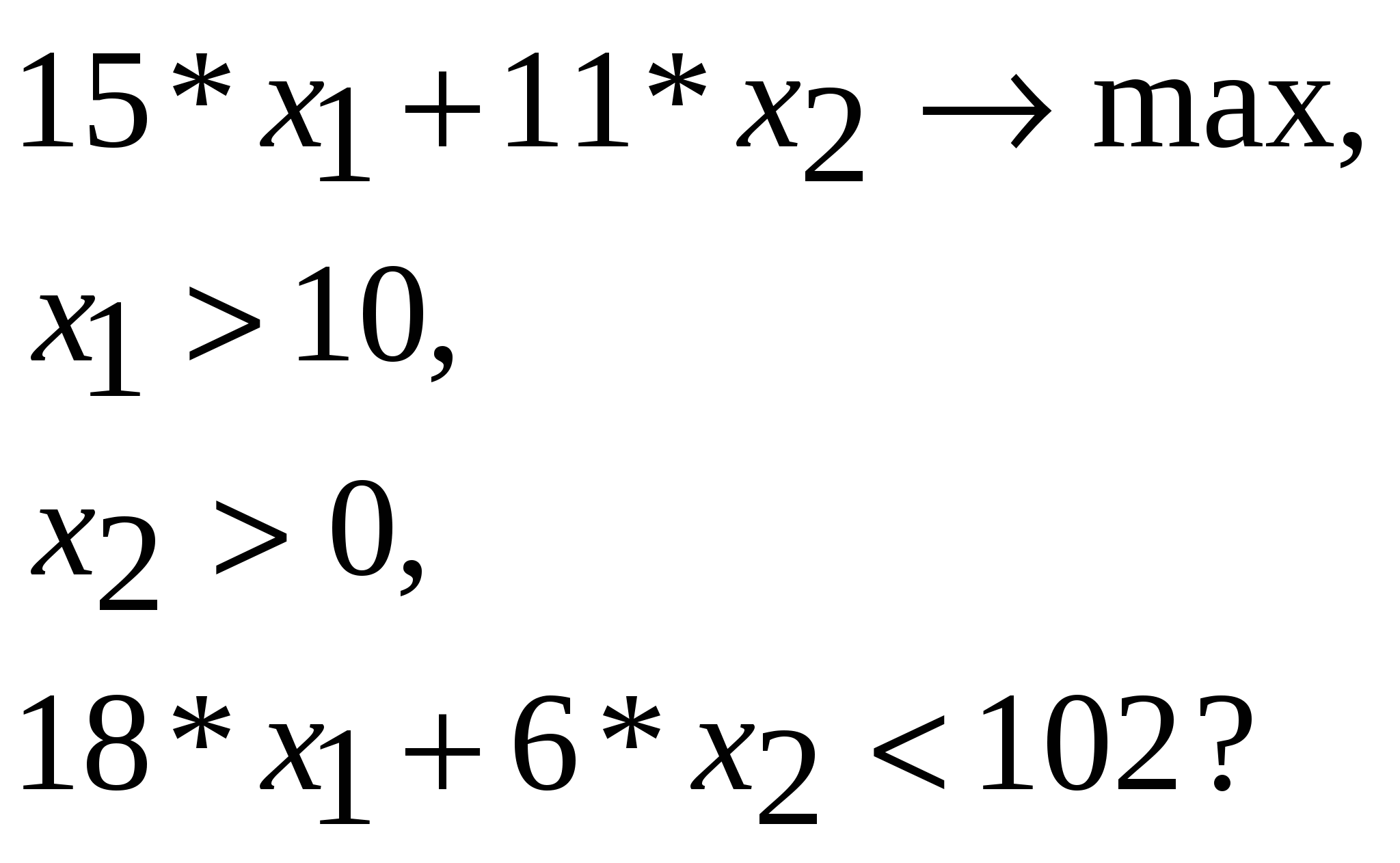Инфор.технологии - Решение задач оптимизации. Федеральное агенство по образованию
 Скачать 1.18 Mb. Скачать 1.18 Mb.
|
|
Задача оптимального использования ресурсов. Постановка задачи. В распоряжении фабрики имеется определенное количество ресурсов: рабочая сила, деньги, сырье, оборудование, производственные площади и т.п. Например, пусть это будут ресурсы трех видов: рабочая сила (80 чел./дней), сырье (480 кг) и оборудование (130 станков/час). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в табл. 14. Таблица 14
Требуется выполнить следующие задания:
Решение. I этап: Составление математической модели прямой ЗЛП Экономико-математическая модель задачи Обозначим через х1, х2, х3, х4 число ковров каждого типа. Целевая функция – это выражение, которое необходимо в данной задаче максимизировать: Ограничения по ресурсам: 7х1 + 2х2 + 2х3 + 6х4 ≤ 80, 5х1 + 8х2 + 4х3 + 3х4 ≤ 480 2х1 + 4х2 + х3 + 8x4 ≤ 130 x1, х2, х3, х4, ≥ 0. II этап: Решение задачи на ЭВМ в среде MS Excel Введем исходные данные (см. рис.30 ) 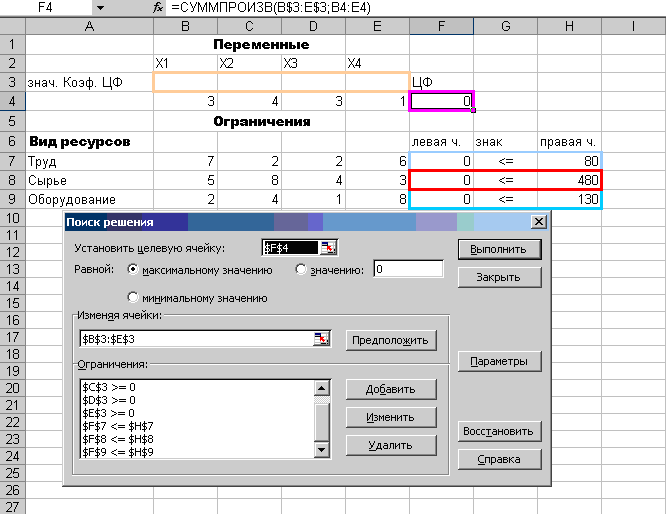 Рис. 30 Введены все условия задачи. После ввода параметров для решения ЗЛП следует нажать кнопку «Выполнить». Полученное решение выглядит следующим образом (рис. 31): 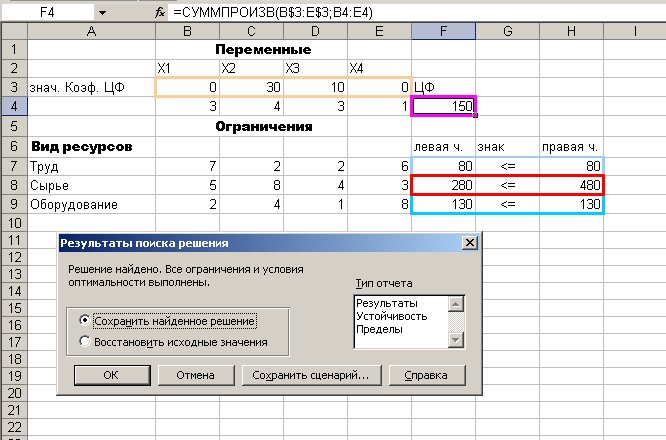 Рис.31 Решение найдено. Как видно из полученного решения, максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы «труд» и «оборудование» будут использованы полностью, а из 480 кг пряжи (ресурс «сырье») будет использовано 280 кг. Создадим отчет по результатам «Поиска решения». Существуют три типа отчетов:
Таблица: Содержание отчета по результатам. 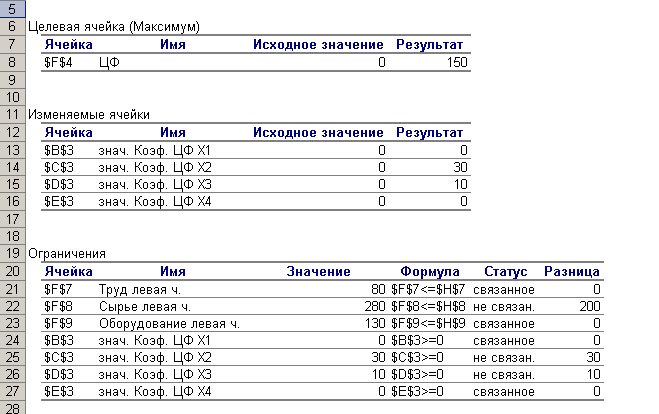 Ш этап: Составление математической модели двойственной ЗЛП Экономико-математическая модель задачи
Число неизвестных в двойственной задаче равно числу функциональных ограничений в исходной задаче. Исходная задача содержит три ограничения: по труду, сырью и оборудованию: Y1 – двойственная оценка ресурса «труд»; Y2– двойственная оценка ресурса «сырье»; Y3 – двойственная оценка ресурса «оборудование»; 2. Целевая функция двойственной задачи формулируется на минимум. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи: Необходимо найти такие цены на ресурсы yi, чтобы общая стоимость используемых ресурсов была минимальной. 3. Ограничения. Число ограничений в ДЗЛП равно числу переменных в прямой задаче. В прямой задаче 4 переменных, следовательно, в двойственной задаче должно быть 4 ограничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничений определяет стоимость ресурсов, затраченных на производство единицы продукции. Каждое ограничение соответствует определенному виду продукции: 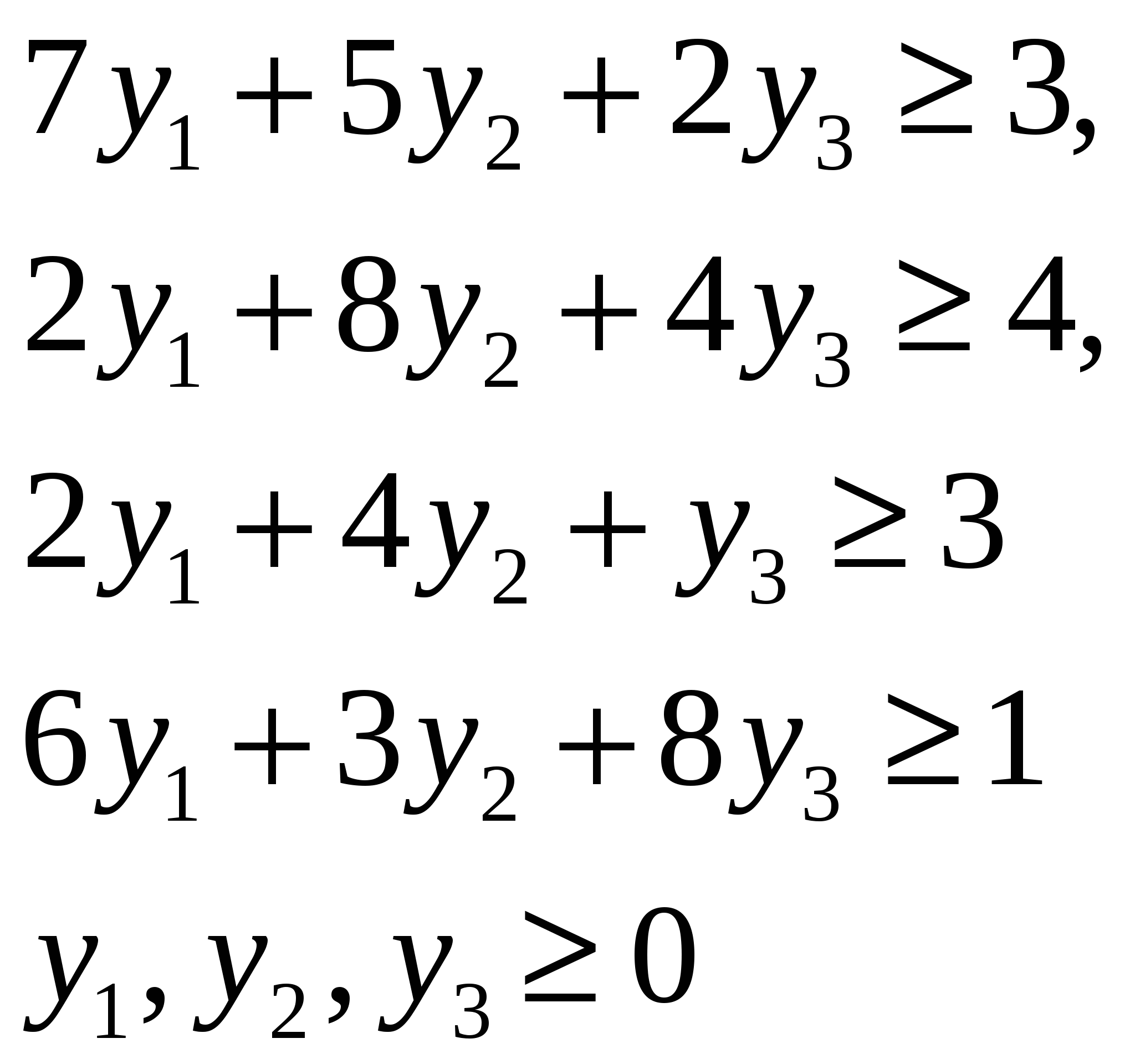 4. Оптимальный план двойственной задачи. Воспользуемся первым соотношением второй теоремы двойственности: 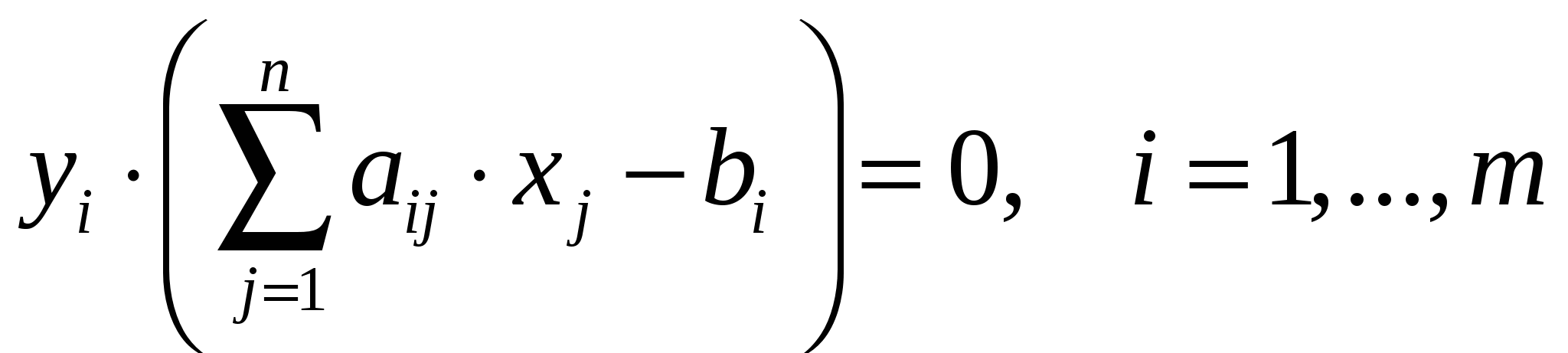 Тогда  Подставим оптимальные значения вектора X в полученные выражения: 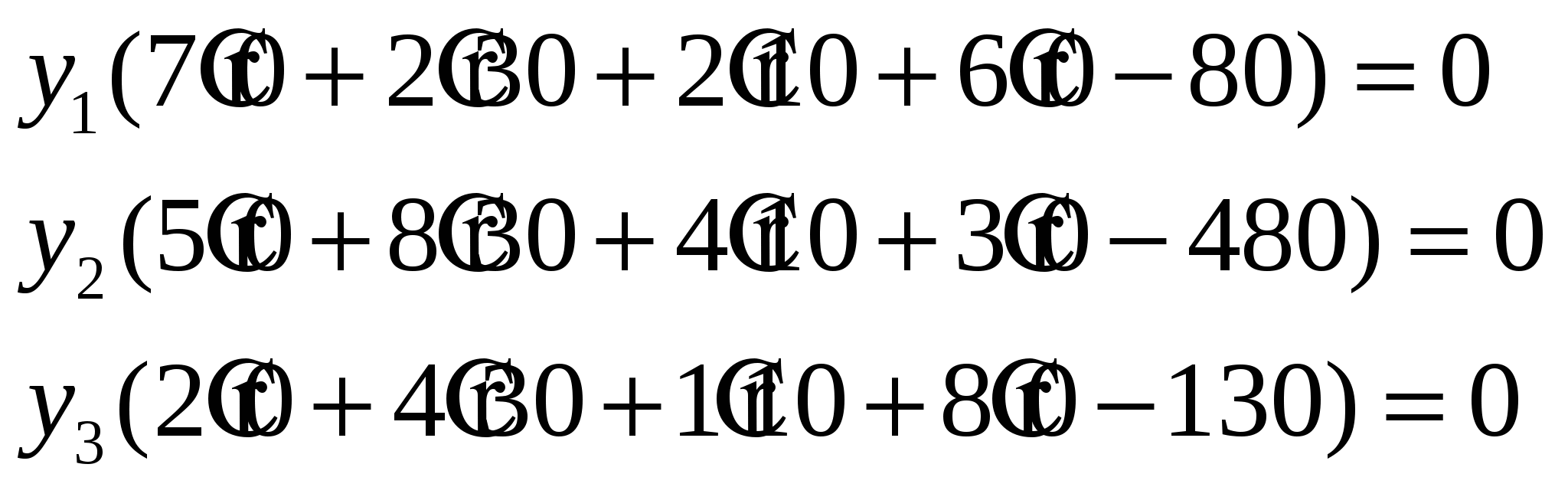 Откуда получаем: 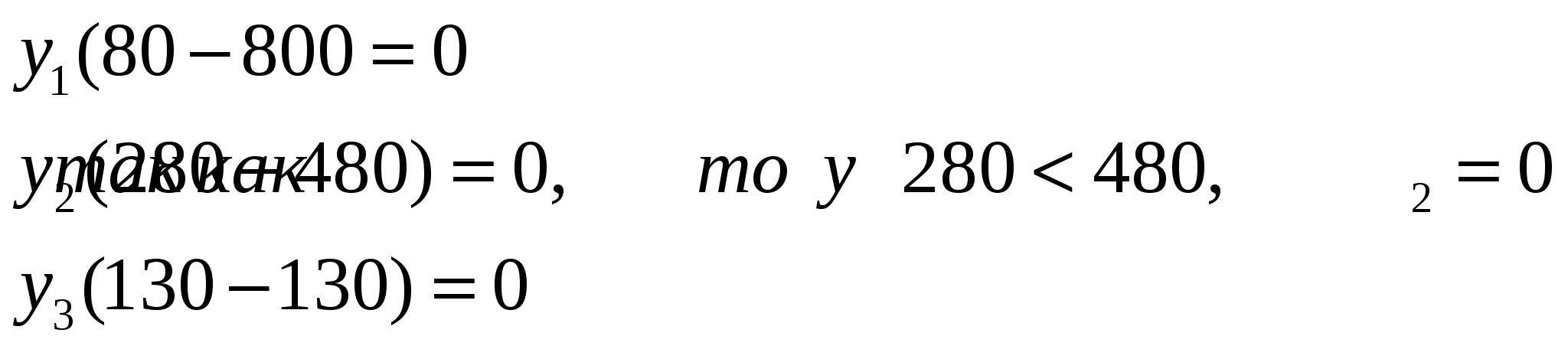 Воспользуемся вторым соотношением второй теоремы двойственности: В нашем случае X2=30>0, X3=10>0, поэтому второе и третье ограничения двойственной задачи обращаются в равенства: 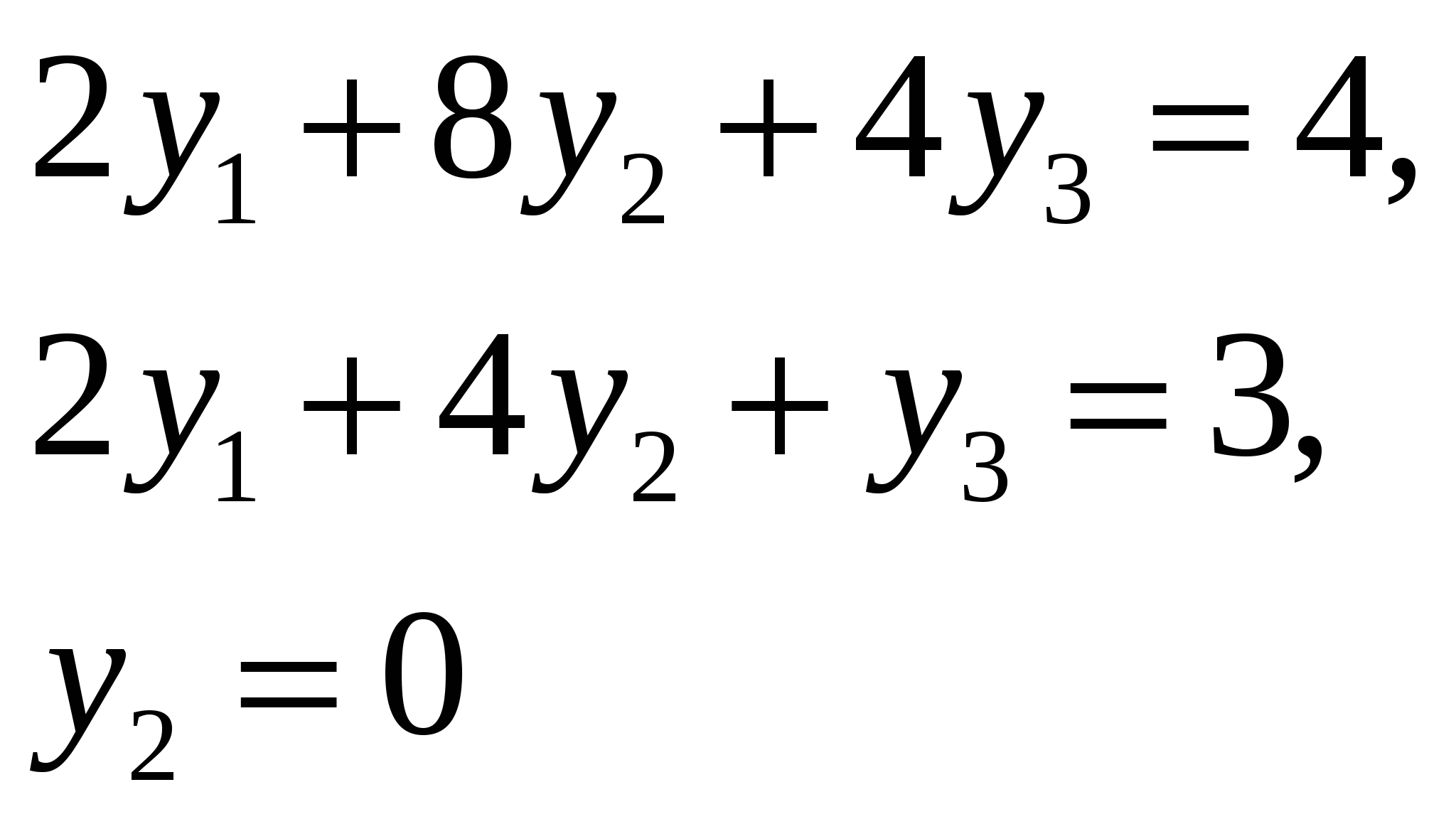 Из полученной системы находим теневые цены ресурсов «труд», «сырье» и «оборудование»: y1=4/3, y2=0, y3=1/3. Проверим выполнение первой теоремы двойственности: Это означает, что оптимальный план двойственной задачи определен верно. Ответ на вопрос о равенстве нулю x1 и x4 будет дан позже. Решение двойственной задачи можно найти, выбрав команду «Поиск решений» «Отчет по устойчивости». Отчет по устойчивости приведен в таблице . 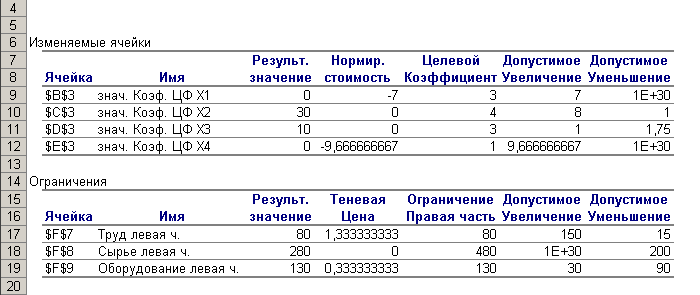 Первая часть таблицы содержит информацию, относящуюся к переменным:
Во второй части таблицы содержится информация, относящаяся к ограничениям:
Анализ полученного оптимального решения исходной задачи с помощью двойственных оценок. Анализ использования ресурсов в оптимальном плане выполняется с помощью второй теоремы двойственности: Если Yi>0, то Если Ресурсы «труд» и «оборудование» имеют отличные от нуля оценки 4/3 и 1/3 – эти ресурсы полностью используются в оптимальном плане и являются дефицитными, т.е. сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям: 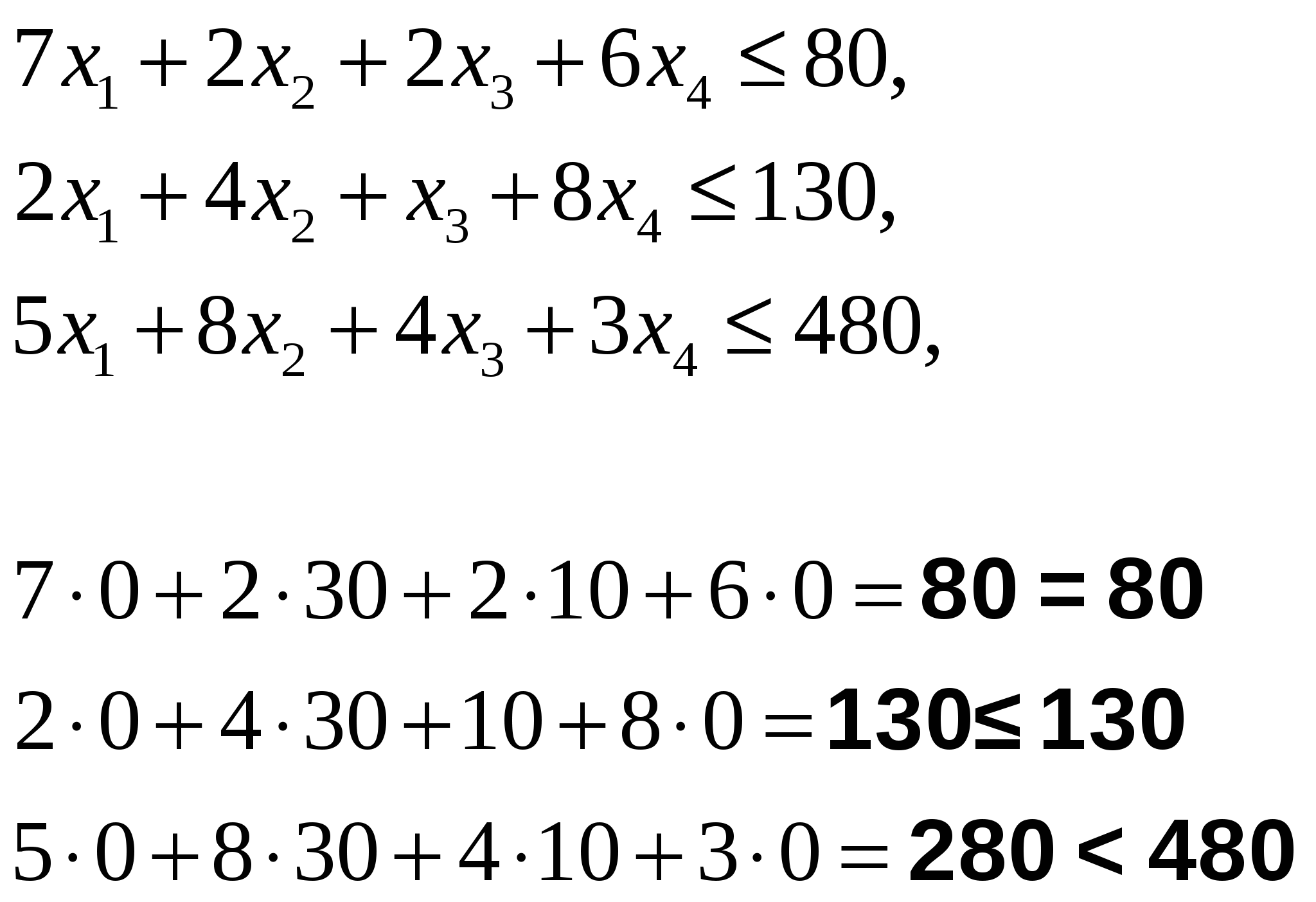 Ресурс «сырье» используется не полностью (280<480), поэтому он имеет нулевую двойственную оценку (Y2=0). Таким образом, этот ресурс не влияет на план выпуска продукции. Общая стоимость используемых ресурсов при выпуске 30 ковров второго вида и 10 ковров третьего вида составляет 150 тыс. руб.: g(Y)=80y1+480y2+130y3= Согласно четвертому ограничению задачи не использованный полностью в оптимальном плане ресурс получает нулевую оценку. Нулевая оценка свидетельствует о его недефицитности. Недефицитность ресурса возникает не из-за его неограниченных запасов ( в задаче они ограничены величиной bi), а из-за невозможности его полного использования в оптимальном плане. Поскольку суммарный расход недефицитного ресурса меньше его общего количества, то план производства им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию f(X). Заметим, что ценность различных видов ресурсов нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, котрая характеризует ценность ресурса только относительно полученного оптимального решения. Анализ эффективности отдельных изделий выполняется на основе соотношений из второй теоремы двойственности: Если Xi>0, то Если Поясним равенство нулю X1 и X4. Если изделие вошло в оптимальный план, то в двойственных оценках оно не убыточно, т.е. стоимость ресурсов, затраченных на производство единицы изделия, равна его цене. Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче – это ковры второго и третьего видов. Если же стоимость ресурсов, затраченных на производство одного изделия, больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В нашей задаче в план выпуска не вошли ковры первого и четвертого видов, поскольку затраты на их выпуск превышают цену на 7 тыс. руб. и 9,666 тыс. руб. соответственно, что видно в «Отчете по устойчивости» в столбце «нормируемая стоимость». Анализ влияния изменения правых частей ограничений на значения целевой функции (чувствительность решения к изменению запасов сырья). Предположим, что запас сырья ресурса «труд» изменился на 12 ед., т.е. теперь он составляет 80+12=92 ед. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных yi в оптимальном плане соответствующей двойственной задачи остаются неизменными. В нашей задаче увеличение запасов ресурса «труд» приведет к увеличению значения целевой функции на 16 тыс. руб. ( Для двойственных оценок оптимального плана существенное значение имеет их предельный характер. Оценки являются точной мерой влияния ограничений на функционал лишь при малом приращении ограничения. Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неизвестных) в плане могут меняться. Поэтому необходимо знать такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, или интервалы устойчивости двойственных оценок, в которых оптимальный план двойственной задачи не менялся бы. Эту информацию можно получить из «Отчета по устойчивости». Таблица. Отчет по устойчивости. 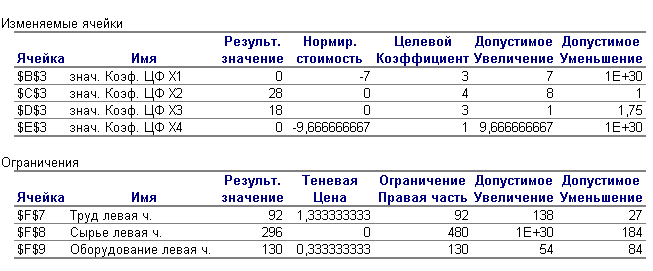 В приведенном фрагменте отчета видно, что запасы дефицитных ресурсов «труд» и «оборудование» могут быть как уменьшены, так и увеличены. Увеличение запаса ресурса «сырье» не влияет на план выпуска продукции. После увеличения запаса ресурса «труд» до 92 чел./час было получено новое решение задачи. Изменение запасов ресурсов в пределах интервалов устойчивости двойственных оценок привело не только к изменению значения целевой функции на 16 тыс. руб., но и к изменению плана выпуска. При этом структура плана не изменилась – изделия, которые были убыточны, не вошли и в новый план выпуска, поскольку цены на ресурсы не изменились. Новый план выпуска составляет 28 ковров второго вида и 18 ковров третьего вида. Изменение общей стоимости продукции на 16 тыс. руб. получено за счет уменьшения плана выпуска на 2 ед. ковров второго вида по цене 4 тыс. руб. (4(28-30)=-8 тыс. руб.) и увеличения на 8 ед. плана выпуска ковров третьего вида по цене 3 тыс. руб. (3(18-100=24 тыс. руб.). 2. Вопросы для самоконтроля:
| ||||||||||||||||||||||||||||||||||