Инфор.технологии - Решение задач оптимизации. Федеральное агенство по образованию

• Название: Федеральное агенство по образованию
• Анкор: Инфор.технологии - Решение задач оптимизации.doc
• Дата: 15.03.2018
• Размер: 1.18 Mb.
• Имя файла: Инфор.технологии - Решение задач оптимизации.doc
• Тип: Методическое пособие; #16692
• страница: 4 из 8

Таблица 11

Неизвестные
– количество усл.ед. кирпичей, перевозимых с i – ого завода на j – ый строящийся объект, i=1,2,3, j = 1,2,3,4.
Целевая функция	Ограничения
S=6*x11+7*x12+3*x13+5*x14+ +1*x21+2*x22+5*x23+6*x24+ +8*x31+10*x32+20*x33+1*x34 (руб.)	x11+x12+x13+x14=100, x21+x22+x23+x24=150, x31+x32+x33+x34=50, x11+x21+x31=70, x12+x22+x32=80, x13+x23+x33=60, x14+x24+x34=90 xi0, i=1,2,3,4, xi – целые числа

II этап: Решение задачи на ЭВМ средствами пакета Excel

1. 
   Формируем диапазон ячеек с исходными данными А1:F7 (см. рис. 22).
   
2. 
   Определяем ячейки, в которых будут содержаться переменные (неизвестные) задачи B11:E13.
   

Примечание: Диапазон неизвестных удобно оформить в виде таблицы.

Присваиваем неизвестным произвольные значения, например, предполагаем, что от каждого завода к каждому объекту необходимо перевезти 1 усл. ед. кирпича (см. рис. 22).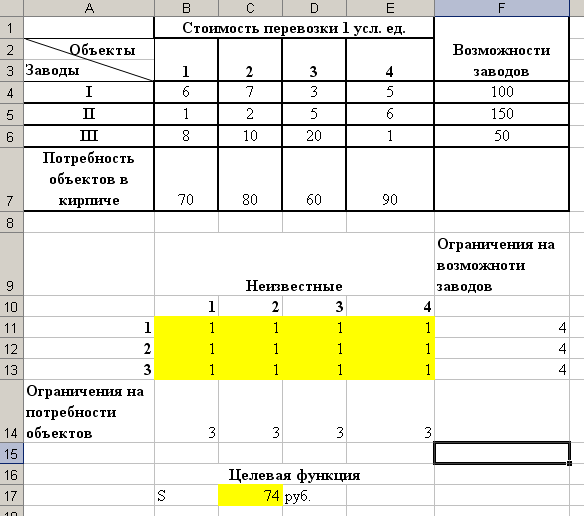



Рис.22 Оформление задачи в Excel

3. 
   Вводим формулу в ячейку, где будет находиться значение целевой функции С17 (см. рис. 23).
   

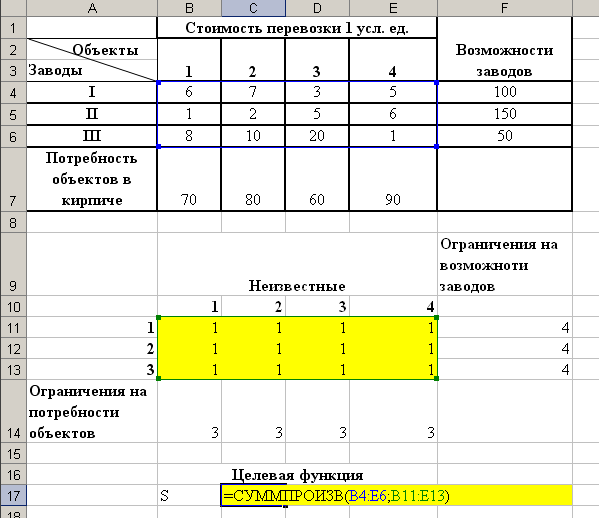Рис.23 Ввод целевой функции

Примечание: Для удобства ввода рекомендуется воспользоваться функцией СУММПРОИЗВ() (Перемножает соответствующие элементы заданных массивов и возвращает сумму произведений.).

Аргументами функции являются массив со стоимостями перевозок В4:Е6 и массив с неизвестными В11:Е13.

4. 
   Вводим зависимости для ограничений (см. рис.24).
   

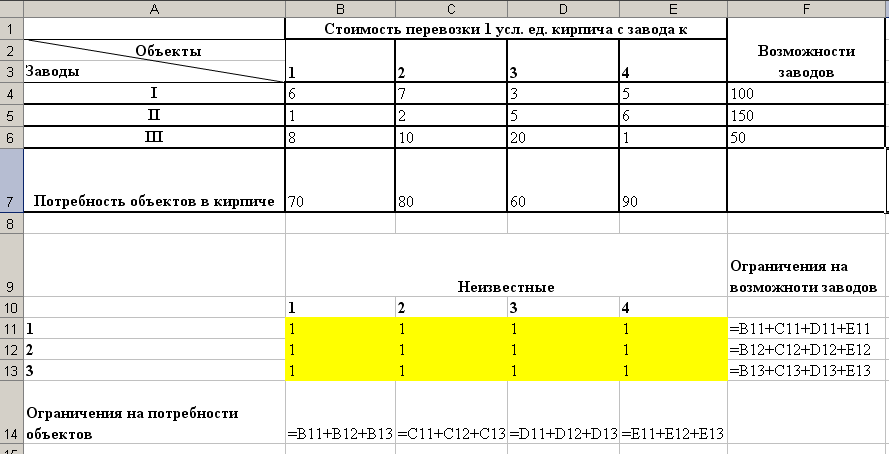Рис.24 Ввод ограничений

Примечание: В ячейках F11:F13 и B14:E14 занесены левые части ограничений, правые части ограничений содержаться в ячейках F4:F6 и B7:E7.

Примечание: Ограничения 20 и 21 будут учтены в окне Поиск решения.

5. 
   Для получения численного решения задачи используем инструмент Поиск решения (Сервис/Поиск решения).
   

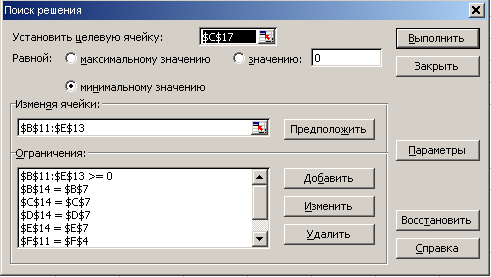Рис.25 Поиск решения

• 
  В окне Установить целевую ячейку указываем адрес ячейки с целевой функцией С17.
  
• 
  В разделе Равной указать Минимальному значению.
  

Примечание: Для заполнения окна Установить целевую ячейку необходимо на листе выделить ячейку, в которой содержится значение целевой функции.

• 
  В окно Изменяя ячейки вносим адреса ячеек с неизвестными задачи B11:E13.
  

Примечание: Для ввода неизвестных можно нажать кнопку Предположить.

• 
  Для ввода ограничений необходимо перейти в поле Ограничения и нажать кнопку Добавить. В появившемся диалоговом окне Добавление ограничения, последовательно, для каждого неравенства в разделе Ссылка на ячейку указать адрес ячейки, соответствующей левой части ограничения, а в разделе Ограничения – адрес правой части ограничения.
  

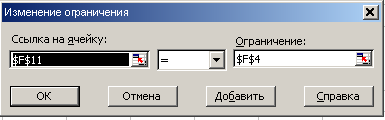Рис. 26 Ввод ограничения 1

Примечание: Ограничения 14-19 вводятся аналогично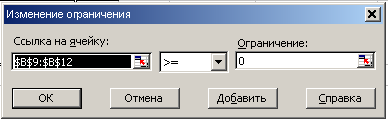



Рис. 6 Ввод ограничения 8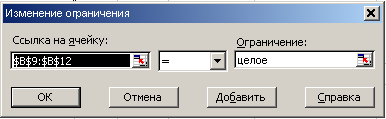



Рис. 7 Ввод ограничения 9

• 
  Нажать кнопку Выполнить.
  

Ответ

В результате решения задачи был получен следующий ответ:

x11=0 (с первого завода на первый объект кирпичи не поставляются),

x12=0 (с первого завода на второй объект кирпичи не поставляются),

x13=60 (с первого завода на третий объект необходимо поставить 60 усл ед. кирпичей),

…

X34=50 (с третьего завода на четвертый объект необходимо поставить 50 усл. ед. кирпичей),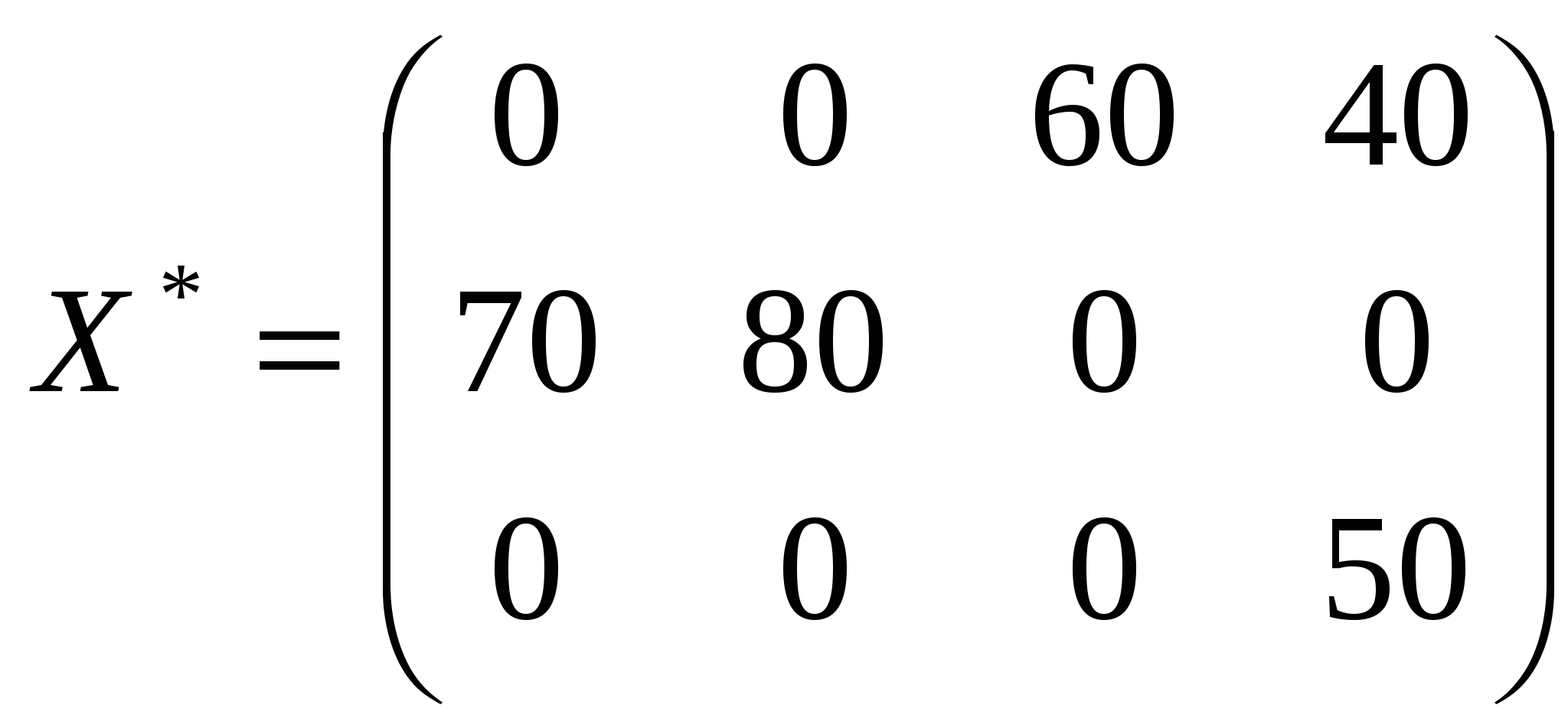

.

При этом минимальная стоимость перевозки будет 660 руб., .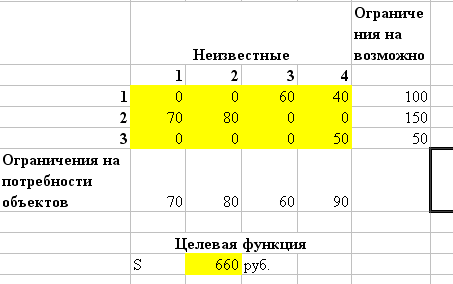



Рис. 29 результат решения задачи

1.3.2.2 Открытая транспортная задача

Постановка задачи

Изменим условие задачи 4 следующим образом: допустим, что потребность первого завода в кирпиче возросла вдвое и составила 140 ед. кирпича в день. Остальные данные остались неизменными.

Таблица 12

	Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту				Возможности заводов
Объекты Заводы	1	2	3	4
I	6	7	3	5	100
II	1	2	5	6	150
III	8	10	20	1	50
Потребность объектов в кирпиче	140	80	60	90

Данная задаче уже является открытой, т.к. 140+80+60+9>100+150+50, т.е. потребности превышают запасы на 160 ед.

Введем нового поставщика - IV завод с возможностью 160 ед.

Так как груз от фиктивного поставщика к фиктивному потребителю не перевозится, то стоимость перевозок полагается равной нулю.

Таблица 12 примет вид:

Таблица 13

	Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту				Возможности заводов
Объекты Заводы	1	2	3	4
I	6	7	3	5	100
II	1	2	5	6	150
III	8	10	20	1	50
IV	0	0	0	0	160
Потребность объектов	140	80	60	90

Данная задача уже является закрытой и решается аналогично задаче
Применение транспортных моделей к решению экономических задач

Алгоритм и методы решений транспортной задачи могут быть применены для решения некоторых классов экономических задач. К таким задачам относятся:

• 
  Задача о назначениях. Она позволяет определить какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности или минимизировать затраты времени.
  
• 
  Задача о закреплении самолетов за воздушными линиями.
  
• 
  Оптимальное закрепление за станками операций по обработке деталей и др.
  

1.3.3 Задача о назначениях

Постановка задачи

Мастер должен расставить трех рабочих для выполнения трех операций. Причем, каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим. Известно сколько минут в среднем тратит каждый из рабочих на выполнение каждой операции. Данные представлены в таблице:

Работники	Работы
	1	2	3
1	10	12	14
2	11	13	14
3	10	9	12

Как распределить рабочих по операциям, чтобы минимизировать суммарные затраты рабочего времени?

Решение

I этап: Составление математической модели

Элементы модели

1. 
   Переменные (неизвестные) задачи
   

Так как в задании требуется распределить рабочих по операциям, то введем переменные , которые будут принимать только два значении:



i=1,2,3, j = 1,2,3,.

В итоге мы имеем 9 неизвестных.

2. 
   Целевая функция V
   

Цель задачи – минимизировать суммарные затраты рабочего времени. Т.к. время выполнения каждым рабочим каждой операции известно, то можно составить целевую функцию.

V будет иметь вид:

V=10*x11+12*x12+14*x13+

+11*x21+13*x22+14*x23+

+10*x31+9*x32+12*x33 (мин.)

3. 
   Ограничения
   

Так каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим, то на неизвестные накладывается ряд ограничений:
Каждый рабочий выполняет только одну операцию

x11+x12+x13=1, (22)

x21+x22+x23=1, (23)

x31+x32+x33=1, (24)

Каждая операция выполняется только одни рабочим

x11+x21+x31=1, (25)

x12+x22+x32=1, (26)

x13+x23+x33=1, (27)

xi –двоичные (28)

Примечание:

Ограничение 7 представляют собой следующие условие:

Неизвестные
i=1,2,3, j = 1,2,3,.
Целевая функция	Ограничения
V=10*x11+12*x12+14*x13+ +11*x21+13*x22+14*x23+ +10*x31+9*x32+12*x33 (мин.)	x11+x12+x13=1, x21+x22+x23=1, x31+x32+x33=1, x11+x21+x31=1, x12+x22+x32=1, x13+x23+x33=1, xi –двоичные

Численное решение задачи в Excel аналогично решению транспортной задачи.
1.3.4 Двойственность в задачах линейного программирования.

Анализ полученных оптимальных решений.

Каждой задаче линейного программирования соответствует двойственная задача.

Первоначальная задача называется исходной или прямой.

Переменные двойственной задачи y_i называются объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми (скрытыми) ценами.

Двойственная задача по отношению к исходной задаче строится по следующим правилам:

1. Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.

2. Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.

3. Если –матрица коэффициентов исходной задачи, то транспонированная матрица будет матрицей коэффициентов двойственной задачи.

4. В задаче на максимум все ограничения имеют знак (=), а в задаче на минимум все ограничения имеют знак .

5. Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.

Модель исходной (прямой) задачи может быть записана следующим образом: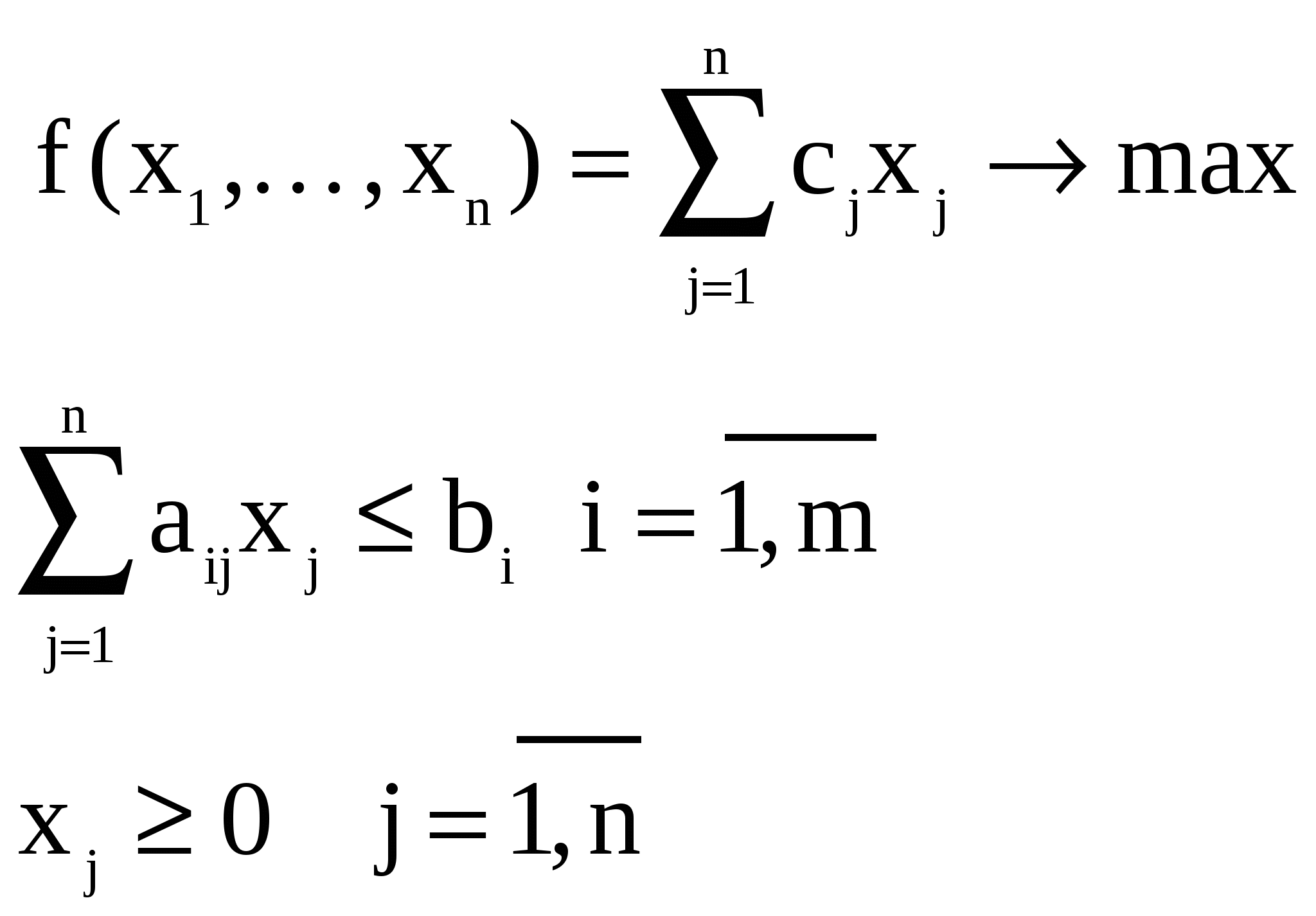


а модель двойственной задачи в этом случае –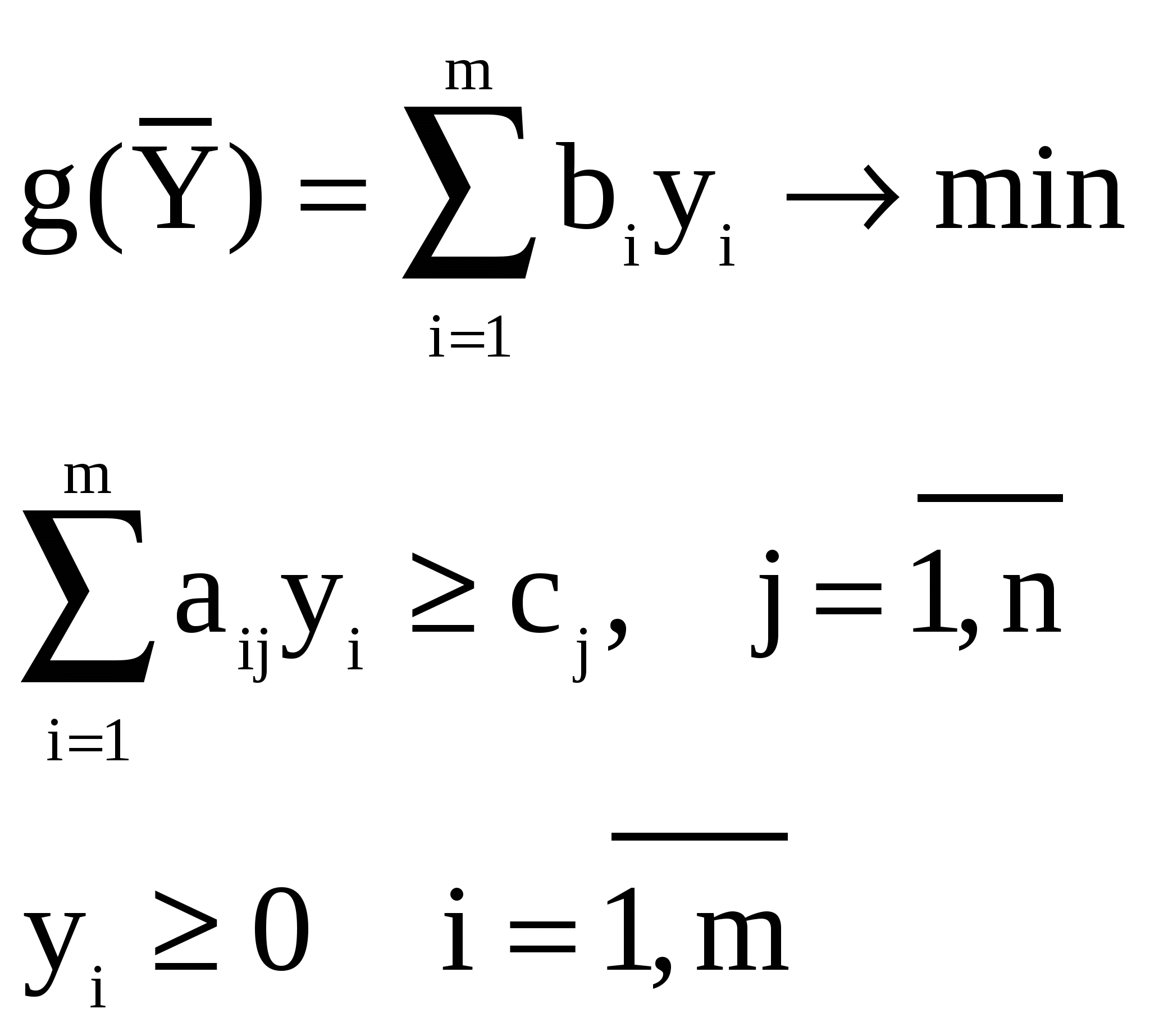



Теоремы двойственности:
Первая теорема двойственности. Для взаимно двойственных задач имеет место один из трех случаев:

1. Если существует решение одной задачи, то существует решение и второй задачи. Значения целевых функций на оптимальных решениях обеих задач равны .

2. Если решение одной задачи неограниченно, то другая задача несовместна.

3. Обе задачи несовместны.

Вторая теорема двойственности.

Пусть 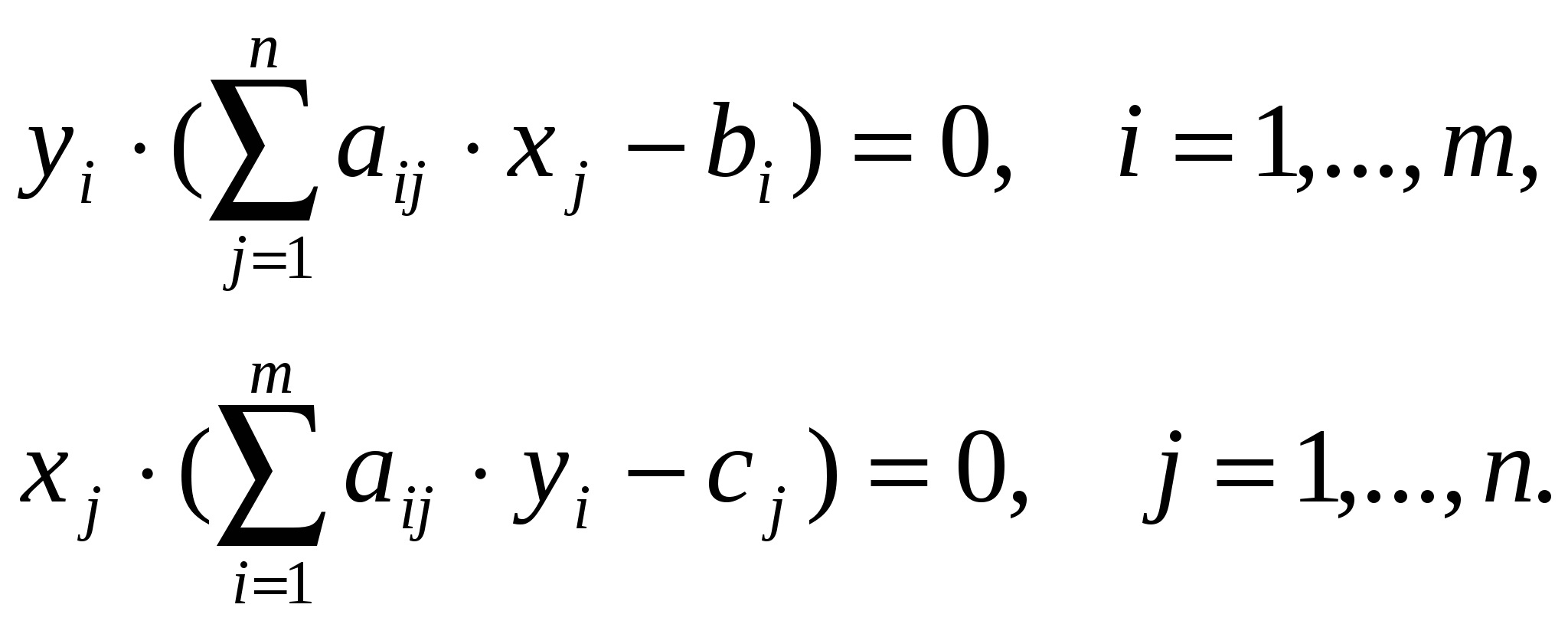- допустимое решение прямой задачи, а - допустимое решение двойственной задачи. Чтобы данные решения были оптимальными, необходимо и достаточно, чтобы выполнялись следующие соотношения:

(29)

Имеет место и обратное свойство: если допустимые значения переменных удовлетворяют соотношениям (1), то они являются оптимальными решениями обеих задач.
Теорема об оценках (третья теорема двойственности).

Значения переменных y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений – неравенств прямой задачи на величину целевой функции этой задачи:

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи y_i в оптимальном плане называют объективно обусловленными, или двойственными оценками. Они даются в строке оценок последней симплекс-таблицы по графам дополнительных переменных. Рассмотрим экономическую интерпретацию двойственной задачи на следующем примере.