Раздел Изменяемые ячейки
Столбец
|
Значение
|
Комментарии и примеры
|
Ячейка
|
Адреса ячеек с неизвестными
|
|
Имя
|
Имена неизвестных
|
|
Результирующее значение
|
Оптимальные значения неизвестных, полученные в ходе решения задачи.
|
Равенство нулю переменных х2, х3, х4означает, что данная продукция является убыточной, т.е. стоимость ресурсов, затраченных на производство одного изделия, больше чем цена продукта.
|
Нормированная стоимость
|
Если продукт входит в оптимальный план, в столбце Нормированная стоимость для этого продукта стоит 0.
Если продукт не входит в оптимальный план, то в этом столбце стоит отрицательное число, абсолютная величина которого показывает на сколько нужно увеличить прибыль от продажи единицы этого продукта, чтобы он вошел в оптимальный план.
|
Пример:
Продукция второго вида не вошла в оптимальный план. Если увеличить прибыль от продажи продукции на 17 ед., т.е. она составит 25+17=42 ед., то станет выгодно выпускать изделия второго вида и оптимальное решение будет следующим
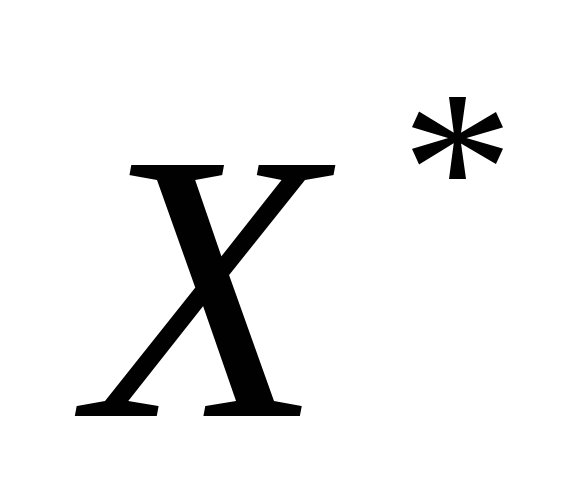 = (0, 8,57, 0, 0), = (0, 8,57, 0, 0),
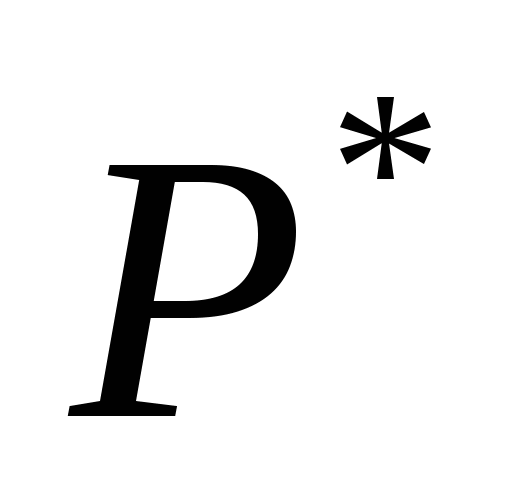 =360 руб. =360 руб.
Аналогичные расчеты можно проделать для 3 – его и 4 – ого продукта.
|
Целевой коэффициент
|
Коэффициенты, стоящие при неизвестных в целевой функции.
|
В данной задаче – прибыль от продажи 1-ой единицы каждого вида продукции.
|
Допустимое
увеличение
Допустимое уменьшение
|
Числа, показывающие, на сколько максимально можно увеличить или уменьшить прибыль от реализации единицы продукции данного вида при сохранении оптимального плана выпуска.
Оптимальное значение ЦФ при этом может изменится.
|
Примечание: Число 1Е+30 (10 +30 - максимально известное компьютеру число) означает, что прибыль можно уменьшать (увеличивать) практически не ограниченно, но при этом оптимальное решение останется прежним.
Анализ полученных значений:
Т.о. получены следующие интервалы устойчивости:
продукция 1 вида – (30+1Е+30, 30-12,142),
продукция 2 вида –
(25+17, 25-1Е+30),
продукция 3 вида –
(8+16, 8-1Е+30),
продукция 4 вида –
(16+32, 16-1Е+30).
Пример:
Для продукции четвертого вида допустимое увеличение 32, а допустимое уменьшение не ограниченно.
Если увеличить прибыль от реализации единицы продукции данного вида на 15, т.е. она составит 16+15=31 руб., при этом оптимальное решение задачи не изменился
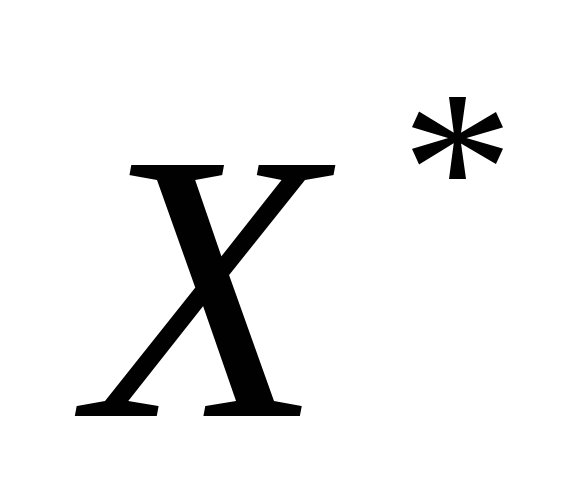 =(12, 0, 0, 0), =(12, 0, 0, 0), 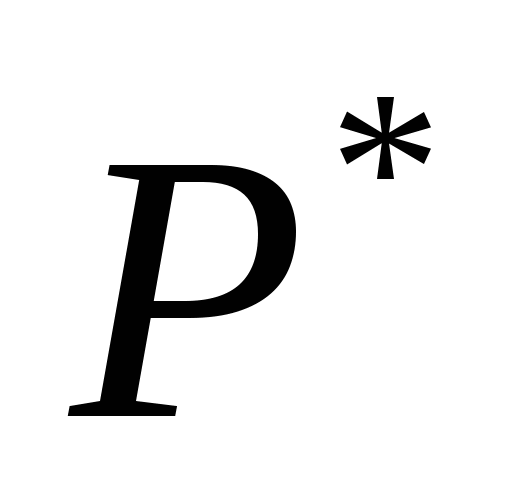 = 360 руб. = 360 руб.
Аналогично, при снижении прибыли на 10 руб. оптимальное решение осталось прежним.
Если прибыль увеличить на 33 руб., т.е. она составит 16+33=49, то оптимальное решение изменится следующим образом:
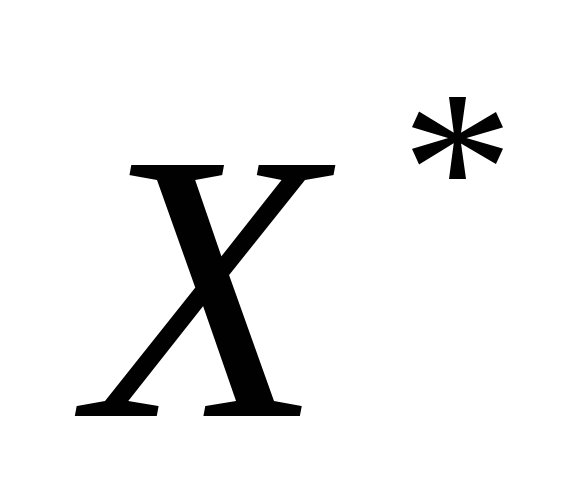 =(0, 0, 0, 7,5), =(0, 0, 0, 7,5), 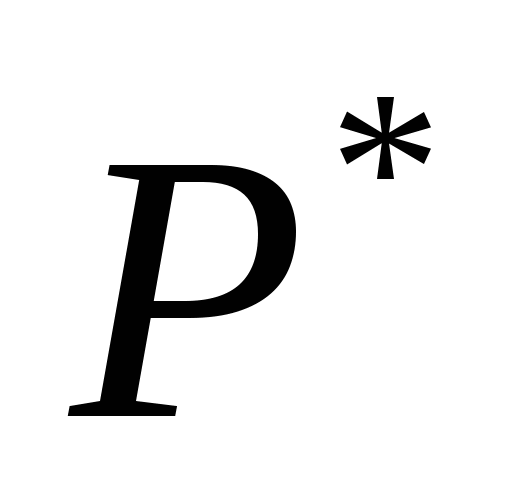 =367,5 руб. =367,5 руб.
|
Таблица 4
Раздел Ограничения
Столбец
|
Примечание
|
Комментарии и примеры
|
Ячейка
|
Адреса ячеек с левыми частями ограничений
|
|
Результирующее значение
|
Значения левых частей ограничений в результате решения задачи
|
|
Теневая цена
|
Теневая цена показывает насколько изменится прибыть от производства всей продукции при увеличении правой части ограничения на 1 единицу (в рассматриваемой задачи – запаса данного ресурса на 1 единицу).
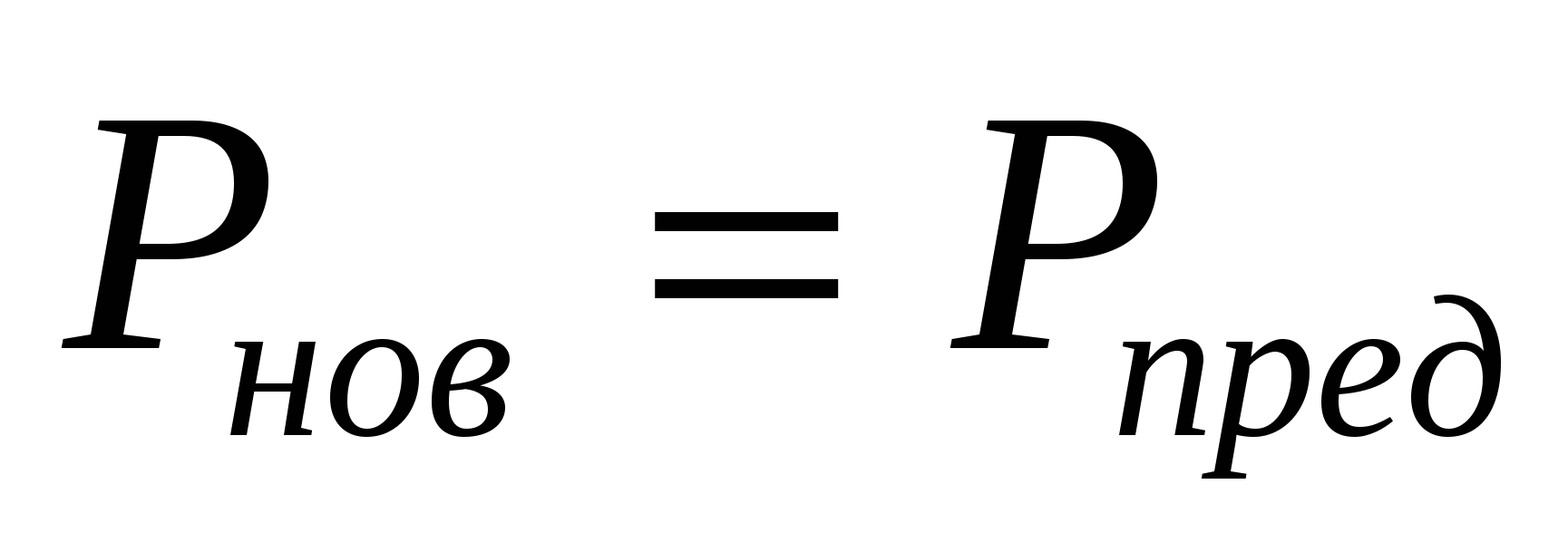 + +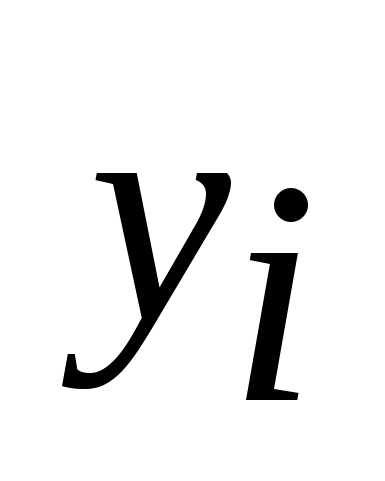
где  - теневая цена. - теневая цена.
Теневая цена, также определяет ценность ресурса для производителя, если она отлична от 0, то ресурс считается дефицитным.
|
Пример:
В нашем случае дефицитным ресурсом является оборудование (т.к. его теневая цена отлична от нуля)  =3. =3.
Также, исходя из ограничения (3), видно, что оборудование использовано на 100 % (левая часть ограничения равна правой), в то время как остальные ресурсы использованы не полностью (левая часть ограничения меньше правой).
Пример:
Если дефицитный ресурс оборудование увеличить на 1 ед., то оптимальная прибыль изменится и станет равной 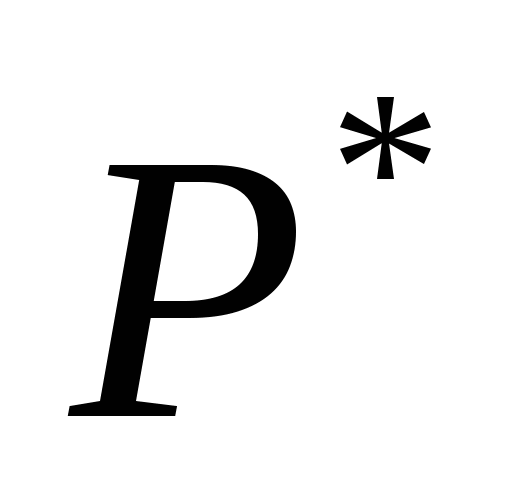 =360+3=363 руб. =360+3=363 руб.
|
Ограничение правая часть
|
Значения правых частей ограничений
|
|
Допустимое
увеличение
|
Число, показывающие, на сколько можно увеличить запасы ресурса при сохранении его теневой цены.
При этом значение целевой функции изменится следующим образом:
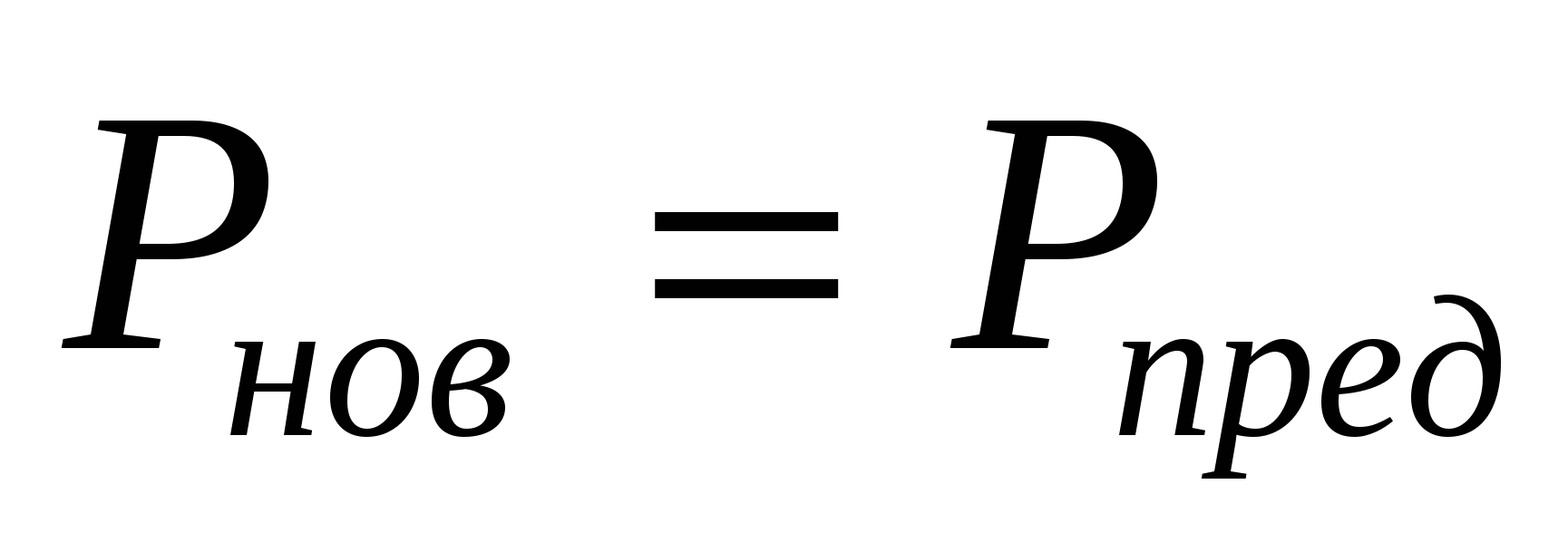 + +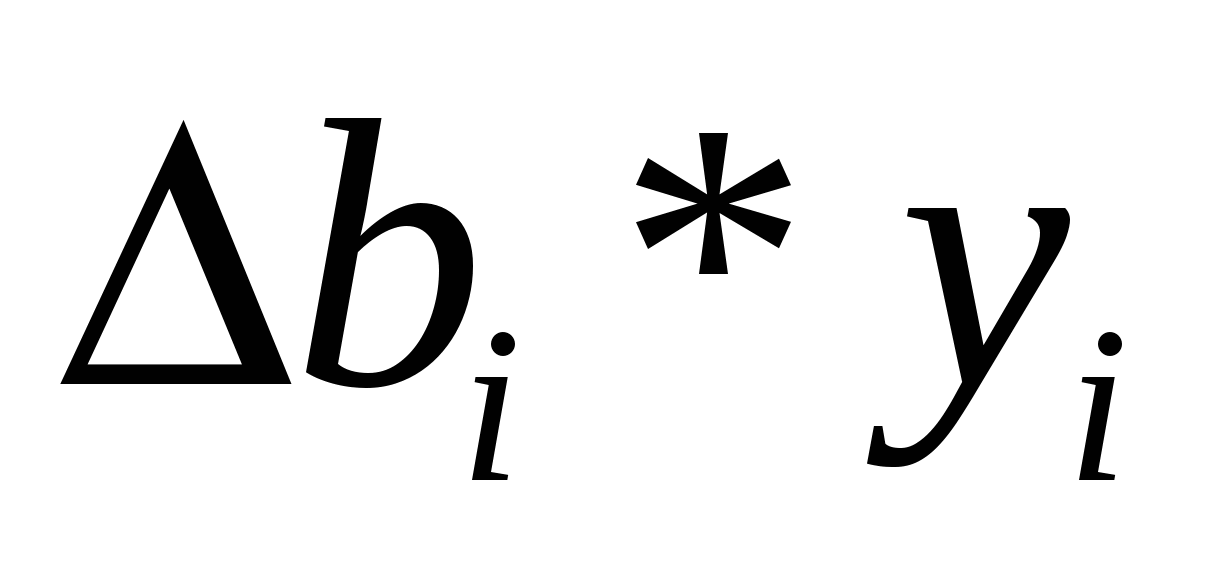 , ,
где 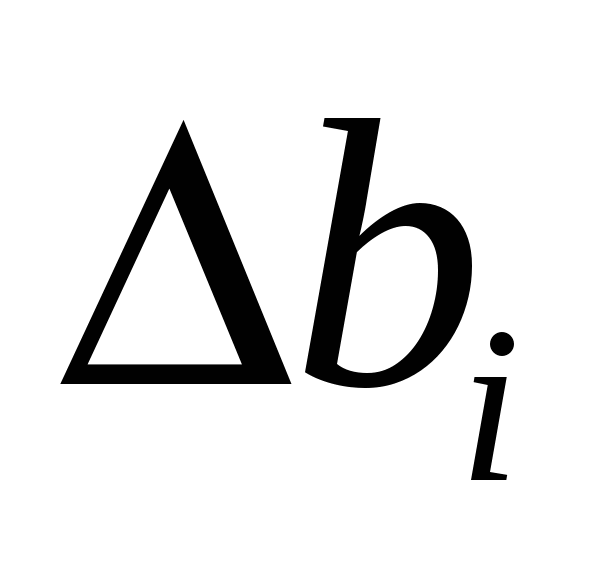 -величина увеличении ресурса, -величина увеличении ресурса,  - теневая цена. - теневая цена.
|
Пример:
Если увеличить ресурс оборудование на 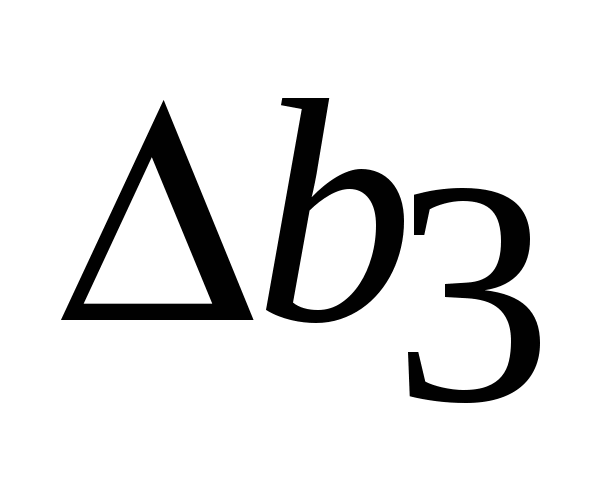 =50 ед., то оптимальная прибыль составит =50 ед., то оптимальная прибыль составит 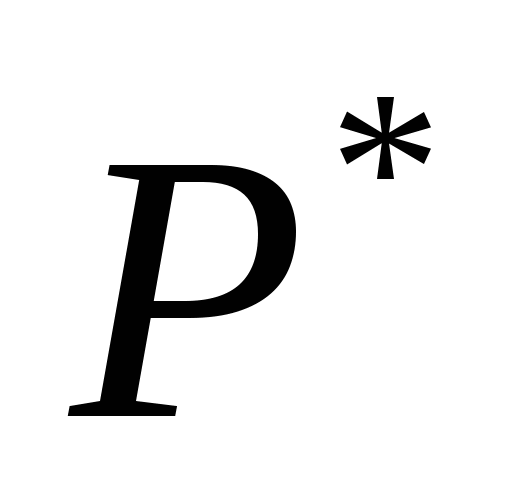 = =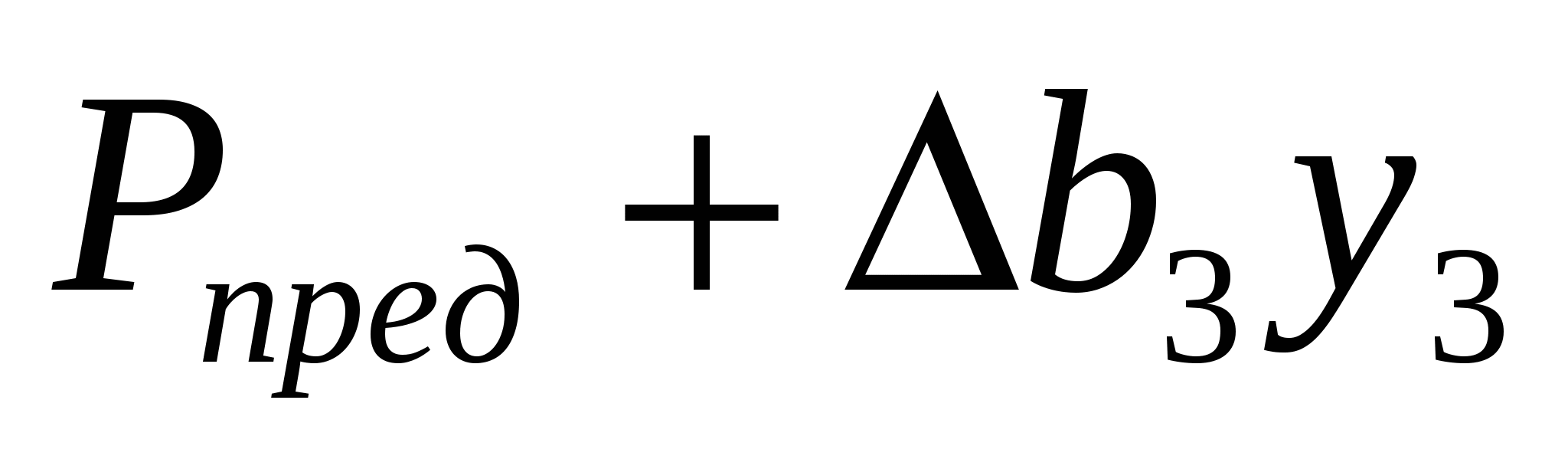 =360+50*3=510 руб. =360+50*3=510 руб.
|
Допустимое уменьшение
|
Число, показывающие, на сколько можно уменьшить запасы ресурса при сохранении его теневой цены.
При этом значение целевой функции изменится следующим образом:
 - -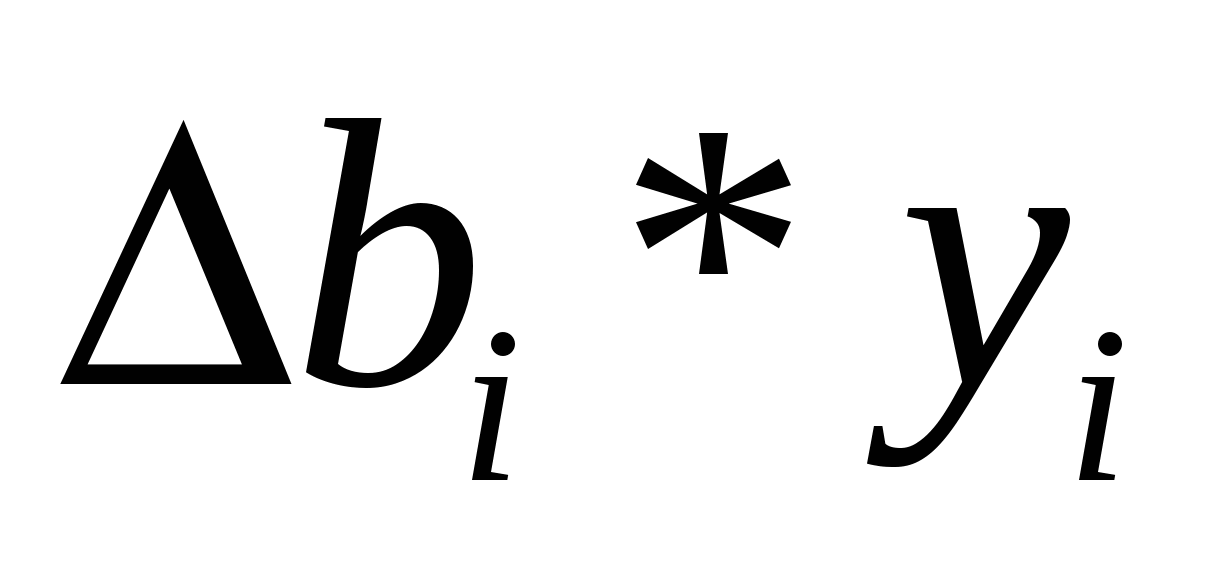 , ,
где 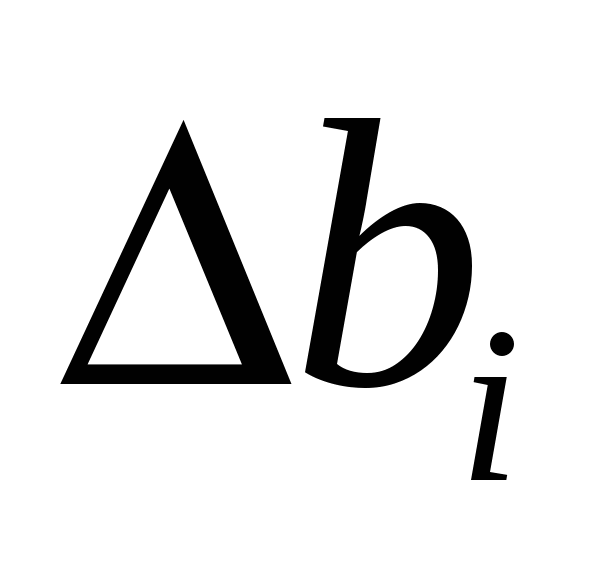 -величина увеличении ресурса, -величина увеличении ресурса,  - теневая цена. - теневая цена.
|
Пример:
Если уменьшить ресурс оборудование на 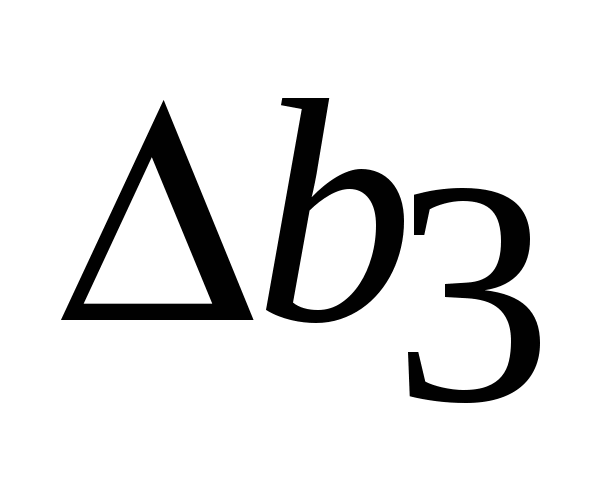 =100 ед., то оптимальная прибыль составит =100 ед., то оптимальная прибыль составит
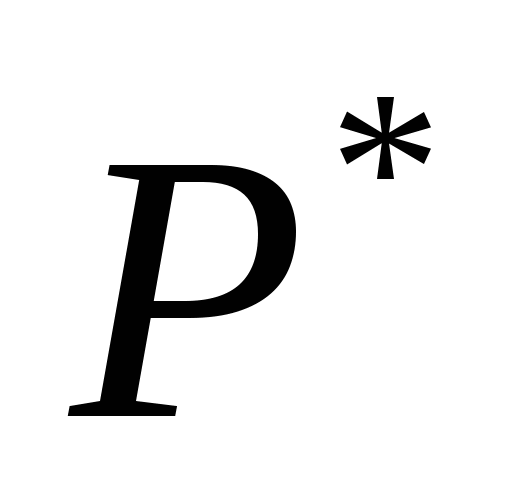 = =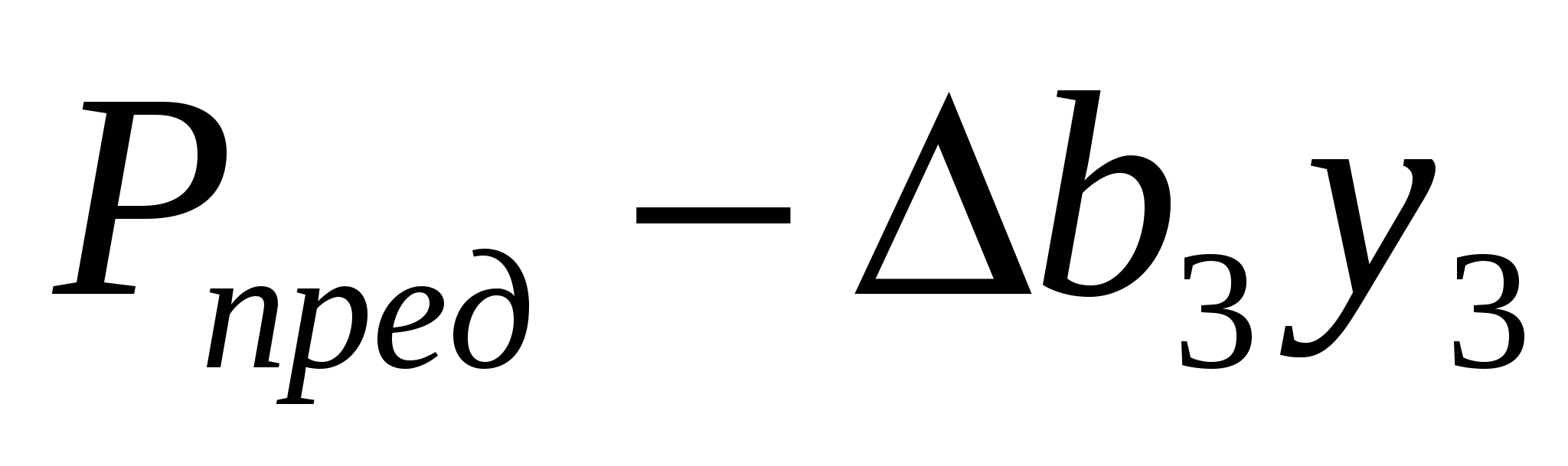 =360-50*3=60 руб. =360-50*3=60 руб.
|
Примечание: Теневые цены и интервал устойчивости изменения запасов каждого из ресурсов, в котором значения теневых цен сохраняются, помогает менеджеру, не решая задачи заново, оценить, запасы какого ресурса нужно увеличить, чтобы максимально увеличить прибыль, и какого будет увеличение прибыли при заданном изменении данного запаса.
1.2 Максимизация годового дохода
Постановка задачи
Вкладчик располагает суммой в размере 50000 руб.
Банки города предлагают следующие проценты по вкладам:
1 банк – 8,5% годовых,
2 банк – 7% годовых,
3 банк – 8% годовых.
Вкладчик хочет распорядиться деньгами следующим образом:
Вся сумма должна быть вложена,
Не менее 55% суммы должно быть вложено во 2 банк,
В 3 банк должно быть вложено по крайней мере столько же, сколько и в 1 банк.
А) Каким образом распределить деньги, чтобы получить максимальный годовой доход?
Б) Каковы интервалы устойчивости процентных ставок банков?
В) Как изменится годовой доход, если вкладчик внесет дополнительные средства?
Решение
I этап: Составление математической модели
Элементы модели
Переменные (неизвестные) задачи
Пусть
x1(руб.) –количество денег, которые вкладчик вложит в 1 банк,
x2(руб.) –количество денег, которые вкладчик вложит во 2 банк,
x3(руб.) –количество денег, которые вкладчик вложит в 3 банк.
Целевая функция
Т.к. цель задачи – максимизировать общий годовой доход (D), то Dбудет иметь вид:
D=x1*8,5%+x2*7%+x3*8% (руб.) (**)
Ограничения
Из предлагаемых процентных ставок банков видно, что чем больше денег будет вложено в 1 банк, тем больше будет годовой доход. Однако, вкладчик выдвигает ряд требований при вложении денег, что приводит к ограничениям на значения неизвестных x1, x2, x3.
x1+x2+x3=50000, (5)
x2 (x1+x2+x3)*55%, (6) (x1+x2+x3)*55%, (6)
x1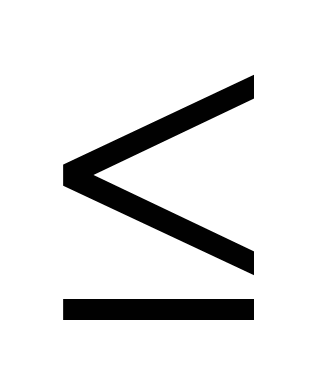 x3, (7) x3, (7)
xi 0, i=1,2,3 (8) 0, i=1,2,3 (8)
Примечание:
В левой части ограничения (1) записана общая сумма денег, которую вкладчик хочет положить в банк под проценты, она должна быть равна 50000 руб.
В ограничении (2) фигурирует знак  , т.к. во второй банк должно быть вложено не менее 55% от общей суммы денег. , т.к. во второй банк должно быть вложено не менее 55% от общей суммы денег.
Аналогично, в ограничении (3) стоит знак 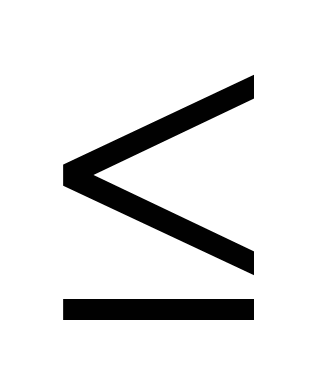 , т.к. в 3 банк вкладывается по крайней мере столько же, сколько и в 1 банк. , т.к. в 3 банк вкладывается по крайней мере столько же, сколько и в 1 банк.
Ограничение (4) представляет собой следующее естественное условие: количество денег, вкладываемое в каждый банк, должно быть не отрицательным.
Таблица 5
Неизвестные
|
x1 (руб.) – количество денег, которые вкладчик вложит в 1 банк,
x2 (руб.) – количество денег, которые вкладчик вложит во 2 банк,
x3 (руб.) – количество денег, которые вкладчик вложит в 3 банк.
|
Целевая функция
|
Ограничения
|
D=x1*8,5%+x2*7%+x3*8% (руб.)
|
x1+x2+x3=50000,
x2 (x1+x2+x3)*55%, (x1+x2+x3)*55%,
x1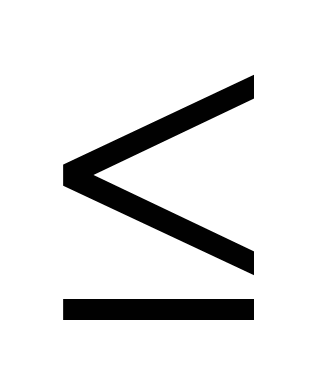 x3, x3,
xi 0, i=1,2,3 0, i=1,2,3
|
II этап: Решение задачи на ЭВМ в среде MS Excel
Формируем диапазон ячеек с исходными данными А1:В4 (см. рис. 11).
Определяем ячейки, в которых будут содержаться переменные (неизвестные) задачи G2:G4 (см.рис. 11).
На начальном этапе присваиваем неизвестным произвольные значения, например, предполагаем, что вклад в каждый банк составил 1 руб. (см. рис. 11).

Рис.11 Оформление задачи в Excel
Вводим формулу в ячейку I7, где будет находиться значение целевой функции (см. рис.12).
Вводим зависимости для ограничений (см. рис.12).
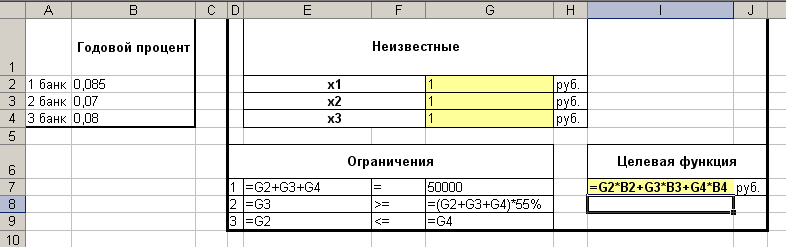  
Рис.12 Ввод целевой функции и ограничений
Примечание: В ячейках E7:E9 занесены левые части ограничений, а в ячейках G7:G9 – правые части.
Примечание: При вводе формул для целевой функции и ограничений необходимо делать ссылки на ячейки созначениями неизвестных G2:G4, а не на ячейки с именами неизвестных E2:E4.
Примечание: Ограничение (4) и знаки неравенств будут учтены в дальнейшем в окне Поиск решения.
Для получения численного решения задачи используем инструмент Поиск решения (Сервис/Поиск решения).
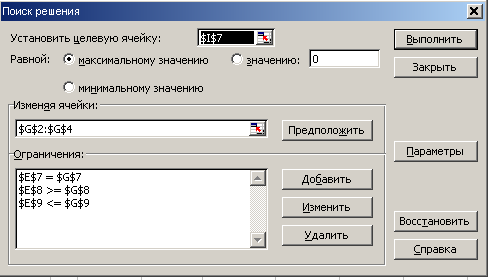
Рис.13 Поиск решения
В окне Установить целевую ячейку указываем адрес ячейки с целевой функцией I7.
В разделе Равной указать Максимальном значению.
Примечание: Для заполнения окна Установить целевую ячейку необходимо поставить курсор в это окно и на листе выделить ячейку, в которой содержится значение целевой функции.
Выбор ячеек с переменными
В окно Изменяя ячейки вносим адреса ячеек с неизвестными задачи G2:G4.
Примечание: Для ввода неизвестных можно нажать кнопку Предположить.
Примечание: Для заполнения окна Изменяя ячейки необходимо поставить курсор в это окно и на листе выделить ячейки, в которых содержатся значения переменных.
Для ввода ограничений необходимо перейти в поле Ограничения и нажать кнопку Добавить. В появившемся диалоговом окне Добавление ограничения, последовательно, для каждого неравенства в разделе Ссылка на ячейку указать адрес ячейки, соответствующей левой части ограничения, а в разделе Ограничения – адрес правой части ограничения.
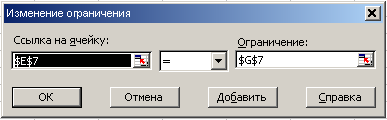
Рис. 14 Ввод ограничения 1

Рис. 15 Ввод ограничения 2
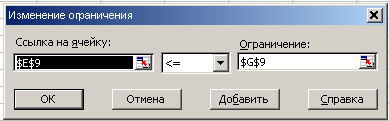
Рис. 16 Ввод ограничения 3
Для установки параметров модели необходимо нажать кнопку Параметры и в появившемся диалоговом окне Параметры поиска решения поставить галочки напротив переключателей Линейная модель и Неотрицательные значения (см. рис. 17).

Рис. 17 Параметры поиска решения
Примечание: Полученная модель будет являться линейной, т.к. целевая функция и неравенства для ограничений являются линейными.
После ввода всех данных необходимо нажать кнопку Выполнить.
На экране появится диалоговое окно Результаты поиска решения (см. рис. 18). Для отображения решения нужно выбрать переключатель Сохранить найденное решение и в окне Тип отчета выделить строку Устойчивость.
Получение данных по устойчивости требуется для проведения анализа решения задачи.
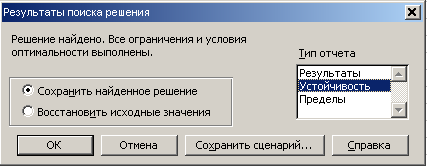
Рис. 18 Результаты поиска решения
Ответ
В результате решения задачи был получен следующий ответ: В первый банк необходимо вложить 11250 руб., во второй банк – 27500 руб., в третий банк – 11250 руб. 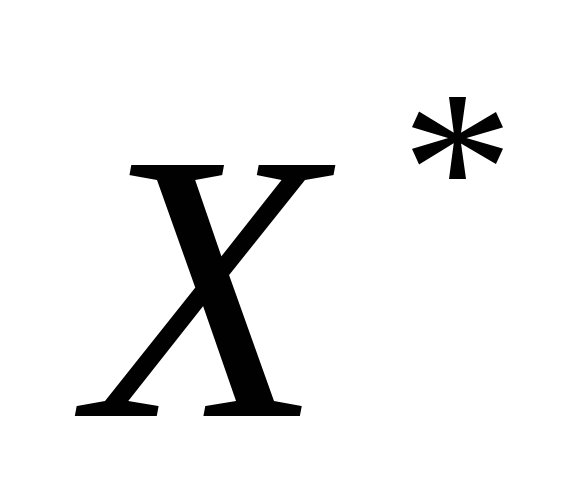 =(11250,27500,11250). =(11250,27500,11250).
При этом максимальный годовой доход составит 3781,25 руб. 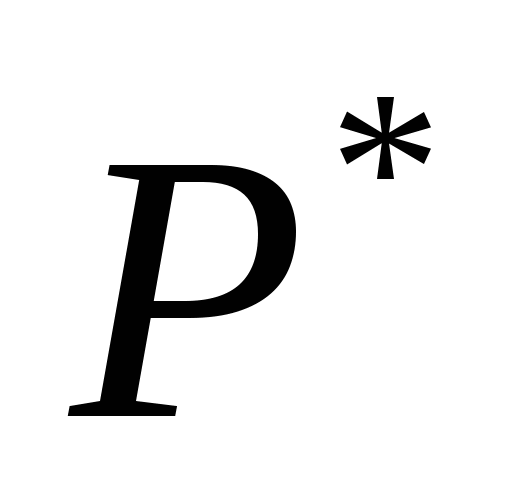 =3781,25. =3781,25.
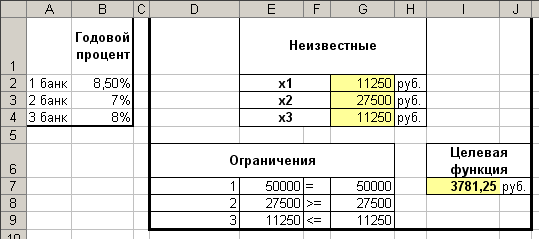
Рис. 19 результат решения задачи
Анализ решения
Используя данные отчета по устойчивости (см. рис. 20) проанализируем полученное решение.
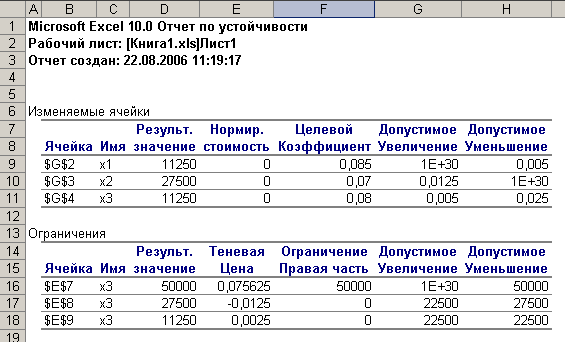
Рис. 20 Отчет по устойчивости
Таблица 6
|
 Скачать 1.18 Mb.
Скачать 1.18 Mb.











