Инфор.технологии - Решение задач оптимизации. Федеральное агенство по образованию

• Название: Федеральное агенство по образованию
• Анкор: Инфор.технологии - Решение задач оптимизации.doc
• Дата: 15.03.2018
• Размер: 1.18 Mb.
• Имя файла: Инфор.технологии - Решение задач оптимизации.doc
• Тип: Методическое пособие; #16692
• страница: 3 из 8

Раздел Изменяемые ячейки

Столбец	Значение	Комментарии и примеры.
Ячейка	Адреса ячеек с неизвестными
Имя	Имена неизвестных
Результирующее значение	Оптимальные значения неизвестных, полученные в ходе решения задачи.
Целевой коэффициент	Коэффициенты, стоящие при неизвестных в целевой функции.	В данной задаче – % ставки банков.
Допустимое увеличение Допустимое уменьшение	Числа, показывающие, на сколько максимально можно увеличить или уменьшить % ставки банков при сохранении оптимального плана. Целевая функция при этом может измениться.	Проводя анализ данных, можно сделать следующие выводы: Годовой процент 1 банка может колебаться в пределах (8%+1Е+30%, 8%-0,5%), 2 банка – (7%+1,25%,7%-1Е+30%), 3 банка – (8%+0,5%, 8%-2,5%), Пример: Предположим, что годовой процент 1 банка увеличился на 1% и составил 8,5%+1%=9,5%. Т.к. для 1 банка увеличение годового процента не ограниченно, то оптимальный план в задаче остался прежним =(11250, 27500,11250), при этом доход D увеличился и составил =3893,75 руб.

Таблица 7

Раздел Ограничения

Столбец	Примечание	Комментарии и примеры
Ячейка	Адреса ячеек с левыми частями ограничений
Результирующее значение	Значения левых частей ограничений в результате решения задачи
Теневая цена	Теневая цена показывает насколько изменится годовой доход при увеличении правой части ограничения на 1 единицу. +, где - теневая цена.	Пример: Предположим, что правая часть 1-ого ограничения увеличилась на 1, т.е. вкладчик вложил 50001 руб. Тогда годовой доход изменится следующим образом: D==3781,25+0,075625= 3893,8279 руб.
Ограничение правая часть	Правые части ограничений
Допустимое увеличение	Число, показывающие, на сколько можно увеличить правые части ограничений сохранении теневой цены. При этом значение целевой функции изменится следующим образом: +, где -величина увеличении ресурса, - теневая цена.	Пример: Если дополнительно вложить еще =10000 руб., то годовой доход изменится следующим образом: D==3781,25+10000*0,075625=4537,5 руб.
Допустимое уменьшение	Число, показывающие, на сколько можно уменьшить правые части ограничений при сохранении теневой цены. При этом значение целевой функции изменится следующим образом: -, где -величина увеличении ресурса, - теневая цена.	Пример: Если уменьшить сумму вклада до 40000руб., =10000 руб., то годовой доход составит: D==3781,25-10000*0,075625=3025 руб.

1.3 Специальные задачи линейного программирования
1.3.1 Задача целочисленного программирования

Решая Задачу 1.1 мы не учитывали того, что количество единиц продукции должно быть целым. Однако не всякую продукцию можно дробить на части.

Рассмотрим исходные данные Задачи 1.1 с тем условие, что в качестве продукции будут выступать ковры 4 – х видов:

Таблица 8

Тип ресурса	Нормы затрат ресурса на один ковер				Наличие ресурсов (ед.)
	1	2	3	4
Сырье	3	5	2	4	60
Рабочее время	22	14	18	30	400
Оборудование	10	14	8	16	120
Прибыль (руб.)	30	25	8	16

В данном случае, математическая модель аналогична математической модели Задачи 1, но добавляется новое условие xi – целые числа.

Таблица 9

Неизвестные
x1 –количество ковров 1 - ого вида, x2– –количество ковров 2 - ого вида, x3 –количество ковров 3 - его вида, x4 –количество ковров 4 - ого вида.
Целевая функция	Ограничения
Р=30*x1+25*x2+8*x3+16* x4(руб.)	3*x1+5*x2+2*x3+4*x460, 22*x1+14*x2+18*x3+30*x4400, 10*x1+14*x2+8*x3+16*x4120, xi0, i=1,2,3,4, xi – целые числа.

Данное условие оформляется в окне Поиск решения следующим образом (см. рис. 21):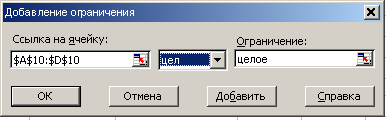



Рис.21 Добавление ограничения

Примечание: Для задач целочисленной оптимизации не предусмотрено вывода отчета по устойчивости.
1.3.2 Транспортная задача

Общая постановка транспортной задачи

Пусть имеется mпоставщиков у которых сосредоточен однородный груз в количестве единиц (), который требуется перевезти nпотребителям в количестве единиц (). Известна стоимость перевозки одной единицы груза от iпоставщика кjпотребителю, она задается матрицей

.

Составить такой план перевозок, при котором стоимость перевозок будет минимальной.
Математическая модель транспортной задачи

Обозначим - количество единиц груза, которое необходимо перевезти от iпоставщика кjпотребителю, тогда стоимость перевозки составит .
Стоимость перевозки всего плана выражается суммой

. (9)

Так как все грузы должны быть перевезены и все потребности должны быть удовлетворены, то получаем следующие ограничения:

(10)

(11)

(12)

Т.о. математическая модель транспортной задачи имеет следующий вид: требуется найти минимум функции (9) при ограничениях (10)-(12).

Теорема 1: Транспортная задача разрешима тогда и только тогда, когда , т.е. сумма запасов и потребностей совпадают.

В случае, если запасы превышают потребности, т.е. , то вводится фиктивный потребитель , потребность которого описывается формулой .

В случае, если потребности превышают запасы, т.е. , то вводится фиктивный поставщик , запасы которого описывается формулой .

Так как груз от фиктивного поставщика к фиктивному потребителю не перевозится, то стоимость перевозок полагается равной нулю .
1.3.2.1 Закрытая транспортная задача

Минимизация стоимости перевозок кирпича

Постановка задачи

Для строительства четырех объектов используется кирпич, изготавливаемый на трех заводах. Ежедневно каждый из заводов может изготавливать 100, 150 и 50 усл. ед. кирпича. Ежедневные потребности в кирпиче на каждом из строящихся объектов равны 70, 80, 60 и 90 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого из заводов к каждому из строящихся объектов, они заданы матрицей С следующего вида: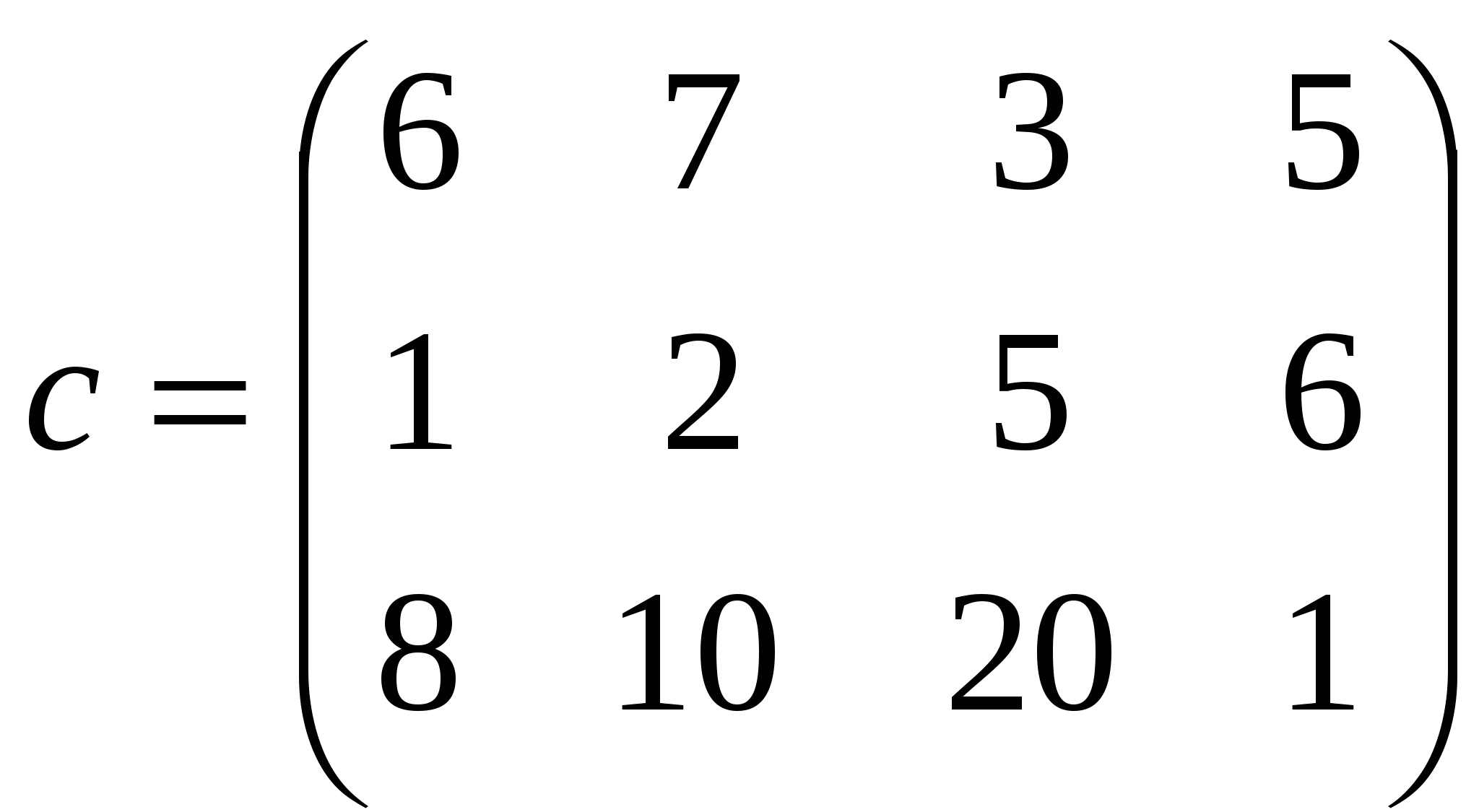

. (***)

Составить такой план перевозок кирпича от заводов к стоящимся объектам, при котором общая стоимость перевозок будет минимальной.
Представим данные задачи в виде следующей таблицы:

Таблица 10

	Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту				Возможности заводов
Объекты Заводы	1	2	3	4
I	6	7	3	5	100
II	1	2	5	6	150
III	8	10	20	1	50
Потребность объектов в кирпиче	70	80	60	90

В данной задаче потребность всех объектов в кирпиче равна запасам всех заводов (70+80+60+90=100+150+50), т.е. она является закрытой, а следовательно разрешима.


Решение

I этап: Составление математической модели

Элементы модели

1. 
   Переменные (неизвестные) задачи
   

В задаче требуется составить оптимальный план перевозок при котором стоимость перевозок будет минимальной, т.е. необходимо определить сколько усл. ед. кирпичей требуется перевозить от каждого завода к каждому строящемуся объекту.

Ведем следующие переменные:

– количество усл.ед. кирпича, перевозимого с i – ого завода на j – ый строящийся объект, i=1,2,3, j = 1,2,3,4.

В итоге мы имеем 12 неизвестных.

Примечание: Например, x12 – количество усл. ед. кирпичей, которые необходимо перевезти с 1 – ого завода ко 2 - ому строящемуся объекту.

2. 
   Целевая функция S
   

Цель задачи – минимизировать стоимость перевозок. Т.к. стоимость перевозки 1 усл. ед. от каждого завода к каждому объекту нам известна (см.*) т.о. Sбудет иметь вид:

S=6*x11+7*x12+3*x13+5*x14+1*x21+2*x22+5*x23+6*x24+

+8*x31+10*x32+20*x33+1*x34 (руб.)

3. 
   Ограничения
   

Так как возможности заводов по ежедневному производству кирпичей ограниченны, а строящиеся объекты имеют ежедневную потребность в кирпиче, то на неизвестные накладывается ряд ограничений:

Ограничения «на производство» кирпича:

x11+x12+x13+x14=100, (13)

x21+x22+x23+x24=150, (14)

x31+x32+x33+x34=50, (15)

Ограничения «на потребности» в кирпиче:

x11+x21+x31=70, (16)

x12+x22+x32=80, (17)

x13+x23+x33=60, (18)

x14+x24+x34=90, (19)
xi0, i=1,2,3,4, (20)

xi – целые числа (21)

Примечание: Ограничения (20) и (21) представляют собой следующие естественные условия: количество перевозимых кирпичей должно быть не отрицательным и целым.