ЛР ЦОС. Лабораторные работы. Конспект лекций по курсу Цифровая обработка сигналов

• Название: Конспект лекций по курсу Цифровая обработка сигналов
• Анкор: ЛР ЦОС
• Дата: 30.09.2021
• Размер: 1.16 Mb.
• Имя файла: Лабораторные работы.doc
• Тип: Конспект лекций; #239395
• страница: 3 из 3

Рисунок 2 – Полюсы системной функции цифрового резонатора

Цифровой фильтр устойчив, если координаты полюсов системной функции фильтра находятся на круге, ограниченном окружностью единичного радиуса с центром в начале координат. Эта окружность показана на рисунке.

Координаты полюсов в экспоненциальной форме описываются следующими соотношениями:

,

где 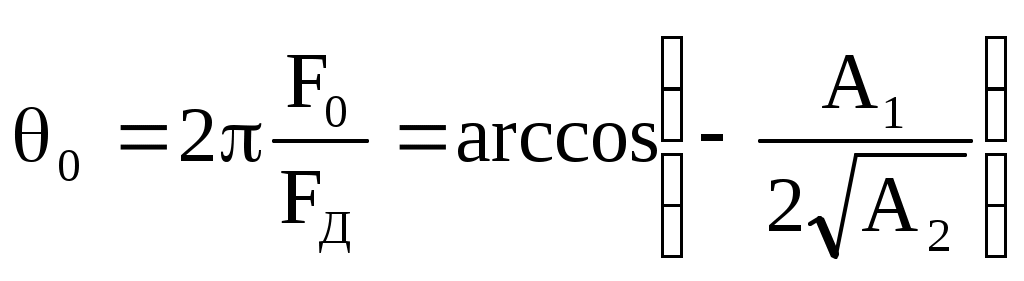, - резонансная частота резонатора.

Подставим в (1) 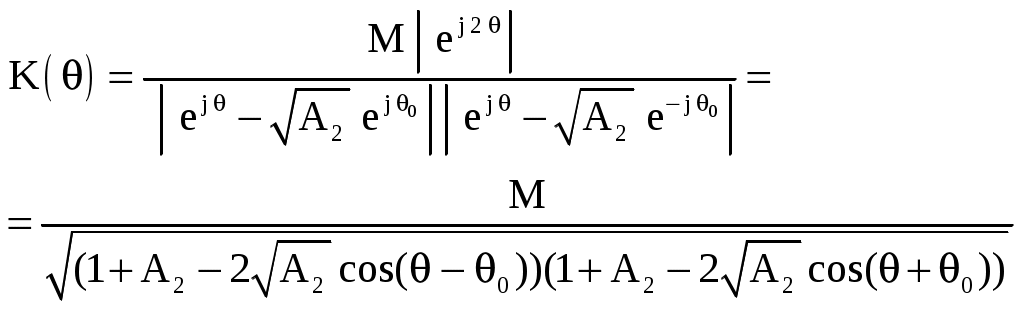, выражения для и и найдем модуль комплексного коэффициента передачи


Обозначим и учте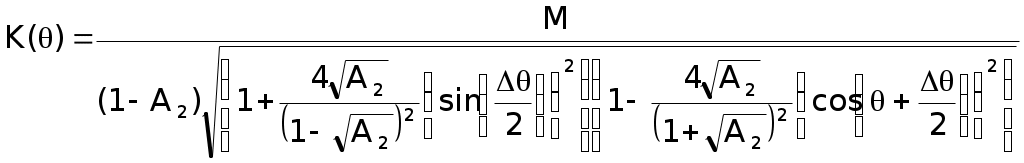м, что



.

Тогда



При 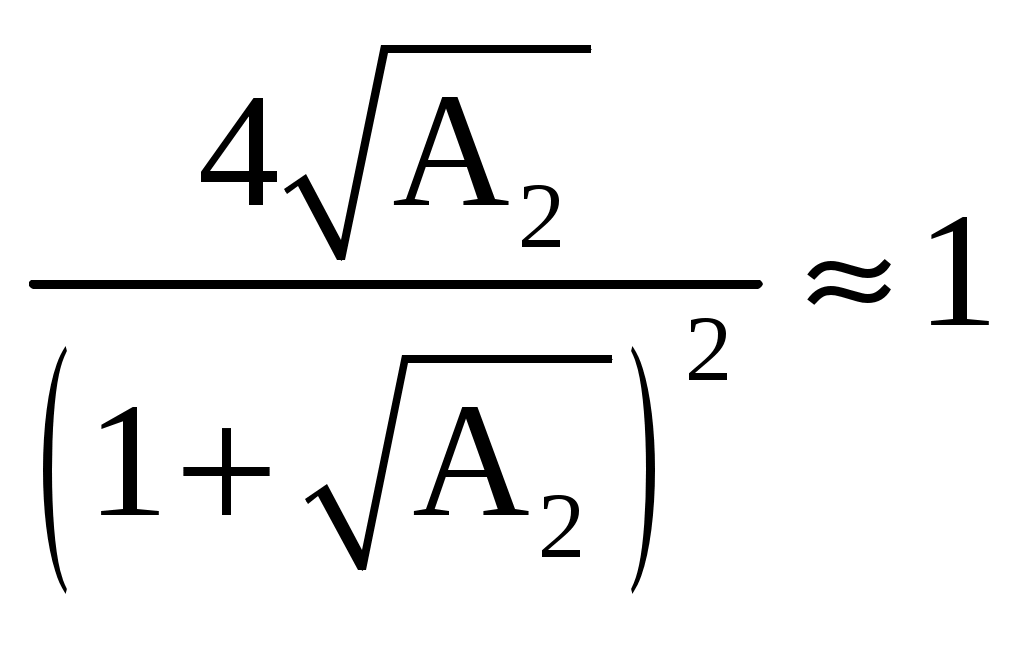с погрешностью, не превышающей 1%, можно принять



Поэтому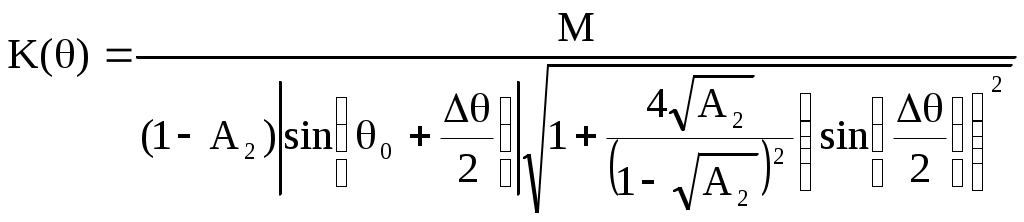


Из последнего соотношения следует, что резонансный коэффициент предачи резонатора равен

. (2)

Из (2) видно, что резонансный коэффициент передачи увеличивается при приближении коэффициента A₂ к единице, прямо пропорционален коэффициенту масштабирования M и зависит от отношения резонансной частоты F₀ к частоте дискретизации F_Д, т.к. ₀ = 2F₀ / F_Д. При удалении резонансной частоты от F_Д / 4 резонансный коэффициент передачи увеличивается.

Из (2) следует также, что для получения одинакового резонансного коэффициента передачи K₀ гребенки резонаторов, настроенных на разные частоты, масштабный коэффициент должен быть выбран равным

. (3)

Разделив K() на K(₀), получим относительный коэффициент передачи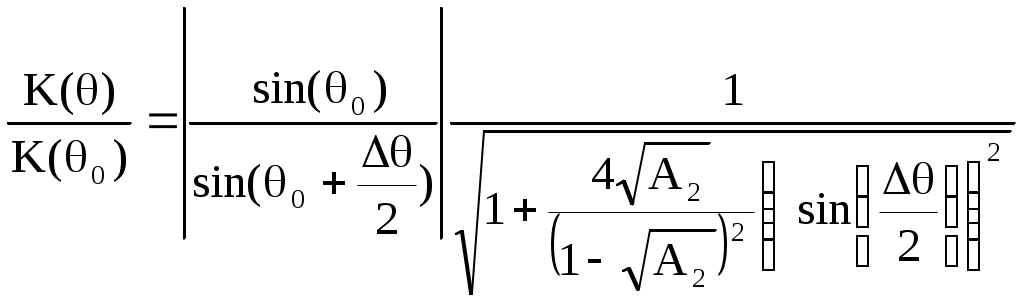
.

Из него видно, что при ₀, отличном от  / 2, АЧХ асимметрична, однако при малых относительных расстройках ( / ₀ <= 0.2) этой асимметрией можно пренебречь. Кроме того при  <= /3 sin( / 2)   / 2.

Поэтому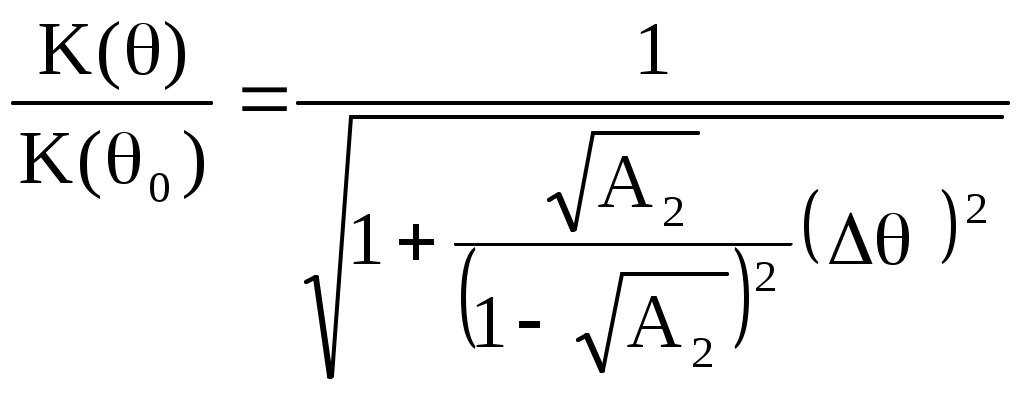

.

Следовательно, при указанных ограничениях АЧХ зависит только от коэффициента A₂ и частоты дискретизации.

Для определения полосы пропускания резонатора П _ при неравномерности  найдем отношение резонансного коэффициента передачи K( ₀) к коэффициенту передачи на границе полосы пропускания K( _g)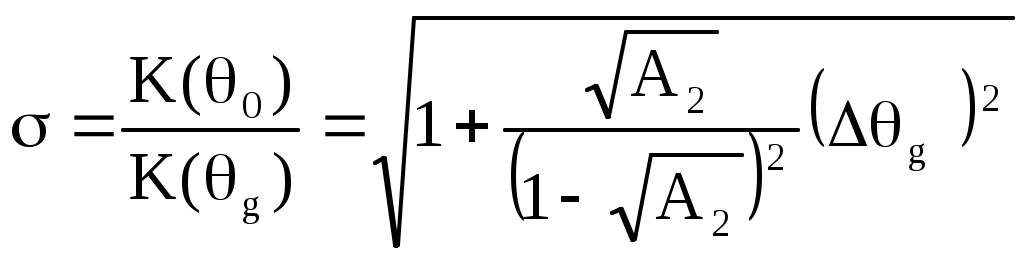


где  _g = П _ / F_Д , откуда
.

Из последнего соотношения видно, что полоса пропускания резонатора прямо пропорциональна частоте дискретизации и уменьшается при приближении значения коэффициента A₂ к единице.

2. 
   Импульсная характеристика резонатора
   

Импульсная характеристика цифрового резонатора может быть найдена как обратное Z-преобразование его системной функции (1)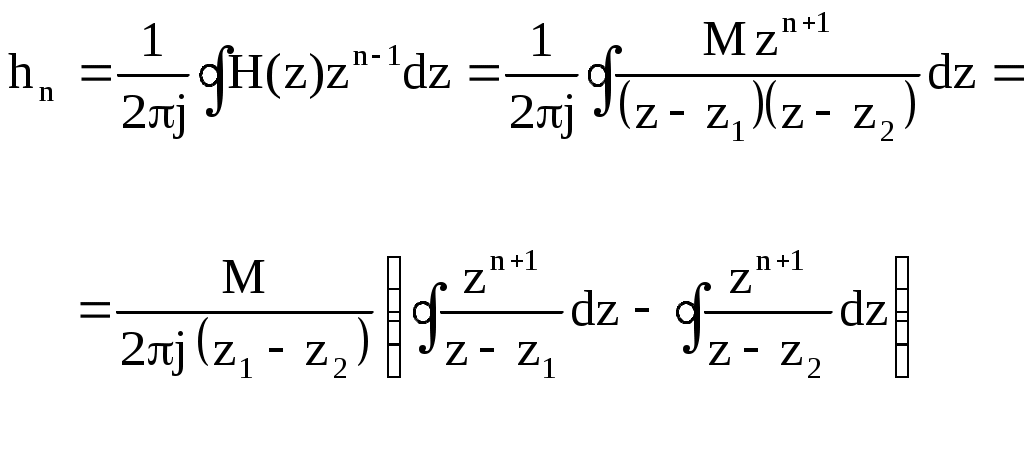



Из теории аналитических функций известно, что интеграл от функции f(z), взятый по замкнутому контуру Г, содержащемуся в области, где функция является однозначной и аналитической, за исключением особых точек однозначного характера, и не проходящему через особые точки, равен произведению суммы вычетов функции относительно всех особых точек, заключенных внутри Г, на 2j.

Если функция f(z) = (z) / (z) и (z) имеет простой нуль при z = a, то

Выч.f(z) = (a) /  ^‘(а),

где  ^‘(z) - производная функции  (z).

В рассматриваемом случае f(z) равна

или ,

поэт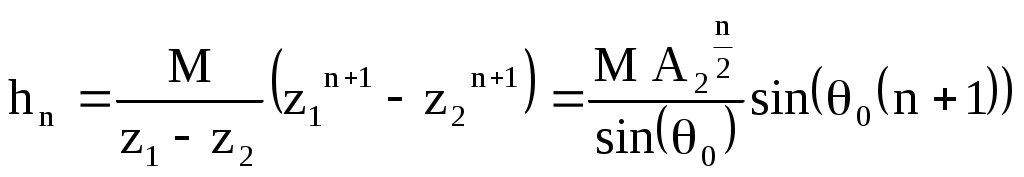ому

.

Таким образом, импульсная характеристика представляет собой затухающее синусоидальное колебание, амплитуда которого зависит от дискретного времени n. Чем ближе A₂ к единице, тем медленнее затухает это колебание. Частота импульсной характеристики равна резонансной частоте резонатора.

Приложение Б

к лабораторной работе №2

Программа исследования АЧХ, ФЧХ и импульсной характеристики.

Имя программы: Rezonator1.sce
1 //Исследование АЧХ, ФЧХ и импульсной характеристики (ИХ)

2 //цифрового резонатора

3 //Ввод исходных данных

4 A1=-0.900;//Коэффициент системной функции

5 A2=0.900; //Коэффициент системной функции

6 nmax=200; //Максимальный номер отсчета

7 //

8 fo0=acos(-A1/(2*sqrt(A2)))/(2*%pi);//Нормированное

9 //значение резонансной частоты

10 M=(1-A2)*abs(sin(2*%pi*fo0));//Масштабный коэффициент

11 j=sqrt(-1);//Мнимая единица

12 delta_fo=0.0001;//Шаг изменения нормированной частоты

13 N=round(0.5/delta_fo);//Количество расчетных точек АЧХ и ФЧХ

14 //Расчет АЧХ и ФЧХ

15 fo=zeros(1:N);

16 K=zeros(1:N);

17 phi=zeros(1:N);

18 for m=1:N

19 fo(m)=delta_fo*(m-1);

20 z(m)=exp(j*2*%pi*fo(m));

21 H(m)=1/(1+A1*z(m)^(-1)+A2*z(m)^(-2));

22 K(m)=abs(H(m));

23 phi(m)=atan(imag(H(m)),real(H(m)));

24 end

25 Ko=M*K; //АЧХ в относительном масштабе

26 //Формирование единичного отсчета

27 n=zeros(1:nmax+1);

28 y=zeros(1:nmax+1);

29 for i=1:nmax+1

30 n(i)=i-1;

31 if i==1 then

32 x(i)=1;

33 else

34 x(i)=0;

35 end

36 end

37 //

38 for i=1:2

39 if i==1 then

40 y(i)=M*x(i);

41 else

42 y(i)=M*x(i)-A1*y(i-1);

43 end

44 end

45 for i=3:nmax+1

46 y(i)=M*x(i)-A1*y(i-1)-A2*y(i-2);

47 end;

48 //Вывод графиков АЧХ, ФЧХ и ИХ

49 xbasc()

50 subplot(2,2,1)

51 plot2d(fo,K,style=[color("blue")])

52 xgrid

53 xtitle('АЧХ при М=1')

54 subplot(2,2,2)

55 plot2d(fo,Ko,style=[color("blue")])

56 xgrid

57 xtitle('АЧХ в относительном масштабе')

58 subplot(2,2,3)

59 plot2d(fo,phi,style=[color("blue")])

60 xgrid

61 xtitle('ФЧХ')

62 subplot(2,2,4)

63 plot2d(n,y,style=[color("red")])

64 xgrid

65 xtitle('Импульсная характеристика')

Приложение В

к лабораторной работе №2
Программа моделирования выходных сигналов трех резонаторов при действии на их входах периодической последовательности единичных отсчетов.

Имя программы: Rezonator2
1 //Наблюдение выходных сигналов трех резонаторов

2 //при действии на их общем входе

3 //периодической последовательности единичных отсчетов

4 //Ввод исходных данных

5 Fd=12;//Частота дискретизации

6 F01=0.5;//Резонансная частота резонатора 1

7 F02=1.0;//Резонансная частота резонатора 2

8 F03=1.5; //Резонансная частота резонатора 3

9 A2=0.9;//Коэффициент системной функции

10 nmax=100;

11 //

12 fo0=zeros(1:3);

13 fo0(1)=F01/Fd; //Нормированная резонансная частота резонатора 1

14 fo0(2)=F02/Fd; //Нормированная резонансная частота резонатора 2

15 fo0(3)=F03/Fd; //Нормированная резонансная частота резонатора 3

16 M=zeros(1:3);

17 A1=zeros(1:3);

18 j=sqrt(-1);

19 delta_fo=0.0001;

20 N=round(0.25/delta_fo);

21 fo=zeros(1:N);

22 K=zeros(N:3);

23 for L=1:3

24 A1(L)=-2*sqrt(A2)*cos(2*%pi*fo0(L)); //Коэффициент системной

25 //функции L-го резонатора

26 M(L)=(1-A2)*abs(sin(2*%pi*fo0(L))); //Масштабный коэффициент

27 //системной функции L-го резонатора

28 end

29 for L=1:3

30 for m=1:N

31 fo(m)=delta_fo*(m-1);

32 z(m)=exp(j*2*%pi*fo(m));

33 H(m,L)=M(L)/(1+A1(L)*z(m)^(-1)+A2*z(m)^(-2));

34 K(m,L)=abs(H(m,L));

35 end

36 end

37 for m=1:N

38 Ko1(m)=K(m,1);

39 Ko2(m)=K(m,2);

40 Ko3(m)=K(m,3);

41 end

42 xbasc()

43 subplot(3,2,1)

44 plot2d(fo*Fd,Ko1,style=[color("blue")])

45 plot2d(fo*Fd,Ko2,style=[color("red")])

46 plot2d(fo*Fd,Ko3,style=[color("green")])

47 xgrid

48 xtitle('АЧХ резонаторов')

49 n0=ceil(Fd/F01);

50 n=zeros(1:nmax+1);

51y=zeros(nmax+1,3);

52 x=zeros(1:nmax+1);

53 //Моделирование периодической последовательности

54 //единичных отсчетов на входах резонаторов

55 for i=1:nmax+1

56 n(i)=i-1;

57 if n(i)/n0-floor(n(i)/n0)==0 then

58 x(i)=1;

59 else

60 x(i)=0;

61 end

62 end

63 subplot(3,2,2)

64 plot2d3(n,x)

65 xgrid

66 xtitle('Сигнал на входах резонаторов')

67 //Моделирование цифровых резонаторов

68 for L=1:3

69 for i=1:2

70 if i==1 then

71 y(i,L)=M(L)*x(i);

72 else

73 y(i,L)=M(L)*x(i)-A1(L)*y(i-1,L);

74 end

75 end

76 for i=3:nmax+1

77 y(i,L)=M(L)*x(i)-A1(L)*y(i-1,L)-A2*y(i-2,L);

78 end

79 end

80 y1=zeros(1:nmax+1);

81 y2=zeros(1:nmax+1);

82 y3=zeros(1:nmax+1);

83 for i=1:nmax+1

84 y1(i)=y(i,1);

85 y2(i)=y(i,2);

86 y3(i)=y(i,3);

87 n(i)=i-1;

88 end

89 subplot(3,2,3)

90 plot2d(n,y1,style=[color("blue")])

91 xgrid

92 xtitle('Сигнал на выходе 1-го резонатора')

93 subplot(3,2,4)

94 plot2d(n,y2,style=[color("red")])

95 xgrid

96 xtitle('Сигнал на выходе 2-го резонатора')

97 subplot(3,2,5)

98 plot2d(n,y3,style=[color("green")])

99 xgrid

100 xtitle('Сигнал на выходе 3-го резонатора')

Приложение Г

к лабораторной работе №2
Программа моделирования цифрового резонатора при действии на

его входе сигнала с помехой.
Имя программы: Rezonator3
1 //Моделирование цифрового резонатора при действии на его входе

2 //сигнала и синусоидальных помех

3 //Ввод исходных данных
4 fc=1;//Частота сигнала

5 f1=0.5;//Частота помехи №1

6 f2=2;//Частота помехи №2

7 Fd=16; // Частота дискретизации

8 nmax=1000;

9 A2=0.99;

10 f0=2.4 //Резонансная частота резонатора

11 A1=-2*sqrt(A2)*cos(2*%pi*fc/Fd); //Коэффициент системной

12 // функции

13 M=(1-A2)*abs(sin(2*%pi*fc/Fd)); //Масштабный коэффициент
14 //Расчет АЧХ резонатора

15 j=sqrt(-1);

16 delta_fo=0.0001;

17 N=round(0.5/delta_fo)+1;

18 fo=zeros(1:N);

19 K=zeros(1:N);

20 for m=1:N

21 fo(m)=delta_fo*(m-1);

22 z(m)=exp(j*2*%pi*fo(m));

23 H(m)=M/(1+A1*z(m)^(-1)+A2*z(m)^(-2));

24 K(m)=abs(H(m));

25 end

26 xbasc()

27 subplot(3,2,1)

28 plot2d(fo*Fd,K,style=[color("blue")])

29 xgrid

30 xtitle('АЧХ')

31 //Формирование сигнала с помехой на входе резонатора

32 n=zeros(1:nmax+1);

33 y=zeros(1:nmax+1);

34 xc=zeros(1:nmax+1);

35 xp=zeros(1:nmax+1);

36 x=zeros(1:nmax+1);

37 for i=1:nmax+1

38 n(i)=i-1;

39 xc(i)=cos(2*%pi*fc*i/Fd); //Сигнал

40 xp(i)=cos(2*%pi*f1*i/Fd)+cos(2*%pi*f2*i/Fd); //Помеха

41 x(i)=xc(i)+xp(i); //Сигнал с помехой

42 end
43 //Определение выходного сигнала резонатора

44 for i=1:2

45 if i==1 then

46 y(i)=M*x(i);

47 else

48 y(i)=M*x(i)-A1*y(i-1);

49 end

50 end

51 for i=3:nmax+1

52 y(i)=M*x(i)-A1*y(i-1)-A2*y(i-2);

53 end;

54 N0=round(5*Fd/fc);

55 n0=zeros(1:N0);

56 xc0=zeros(1:N0);

57 xp0=zeros(1:N0);

58 x0=zeros(1:N0);

59 y0=zeros(1:N0);

60 for k=1:N0

61 n0(k)=nmax-N0+k;

62 xc0(k)=xc(nmax-N0+k);

63 xp0(k)=xp(nmax-N0+k);

64 x0(k)=x(nmax-N0+k);

65 y0(k)=y(nmax-N0+k);

66 end

67 subplot(3,2,3)

68 plot2d(n0,xc0,style=[color("red")])

69 xgrid

70 xtitle('Сигнал на входе резонатора')

71 subplot(3,2,5)

72 plot2d(n0,xp0)

73 xgrid

74 xtitle('Помеха на входе резонатора')

75 subplot(3,2,2)

76 plot2d(n0,x0,style=[color("green")])

77 xgrid

78 xtitle('Сигнал с помехой на входе резонатора')

79 subplot(3,2,4)

80 plot2d(n0,y0,style=[color("red")])

81 xgrid

82. 
    xtitle('Сигнал на выходе резонатора')